Математический анализ. Мат. Анализ. Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования государственный университет управления

• Название: Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования государственный университет управления
• Анкор: Математический анализ
• Дата: 19.03.2022
• Размер: 0.54 Mb.
• Имя файла: Мат. Анализ.doc
• Тип: Образовательная программа; #403778

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение

высшего образования

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»

Институт	открытого образования
Кафедра	математики и информатики

Контрольное задание

по дисциплине	Математический анализ (2)
Вариант №1
Направление подготовки	38.03.01		Экономика
	(код)		(наименование)
Образовательная программа	Экономика
	(название образовательной программы)
Обучающийся
	(фамилия, имя, отчество)
2 курс, Б-Э-20/1	форма обучения		заочная
(курс, номер группы)			(очная / очно-заочная / заочная)
Преподаватель
	(ученая степень, звание, фамилия и инициалы)

Москва – 2022


Содержание

Задача №1 2

Задача №2 4

Задача №3 6

Задача №4 9

Задача №5 11

Задача №6 14

Задача №7 18

Задача №8 20

Задача №9 24

Задача №10 26

Список использованных источников 28

Задача №1

В аналитическом отделе фирмы 6 менеджеров и 14 финансистов. Для выполнения задания случайным образом из списка выбирают 3 человек. Найти вероятность того, что менеджеров среди них будет:

а) ровно два;

б) не менее одного.
Решение

а) ровно два менеджера

Обозначим через А интересующее событие, состоящее в том, что среди отобранных человек окажется ровно два менеджера.

В соответствии с классическим определением вероятности, вероятность события определяется равенством:

, где:

- число элементарных исходов испытания, благоприятствующих появлению события А;

- общее число возможных элементарных исходов испытания.

Общее число возможных элементарных исходов испытания ( ) в данном случае равно числу способов, которыми можно выбрать 3 человек из общего количества сотрудников (из 6+14=20), то есть соответствующему числу сочетаний: .

Число элементарных исходов испытания, благоприятствующих появлению события А ( ), соответствует количеству способов, которыми можно выбрать двух менеджеров (из общего количества менеджеров) и одного финансиста (из общего количества финансистов), то есть: .

Таким образом, искомая вероятность составит:



_{Поскольку:}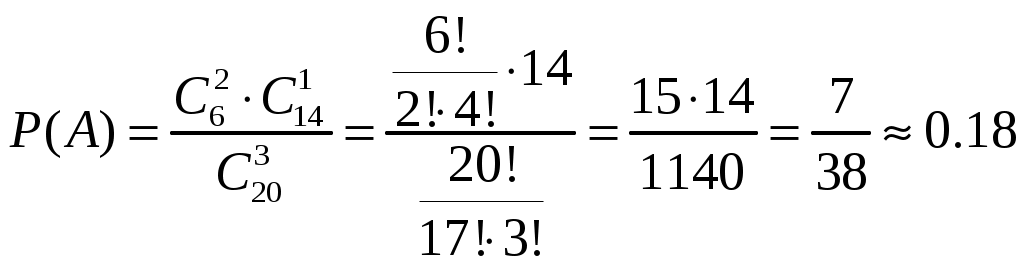

, получаем:



б) не менее одного менеджера

Обозначим через А интересующее событие, состоящее в том, что среди отобранных человек окажется не менее одного менеджера.

Обозначим через событие, состоящее в том, что среди отобранных человек окажется менее одного менеджера, то есть среди отобранных сотрудников менеджеров не будет вовсе.

Очевидно, что данные события противоположные, в связи с чем:

, тогда:



Найдем вероятность того, что среди отобранных человек менеджеров не окажется:



Найдем вероятность искомого события:



Ответ: вероятность того, что среди выбранных 3 человек менеджеров будет ровно два, составляет 0,18; вероятность того, что менеджеров будет не менее одного, составляет 0,68.


Задача №2

Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба первый клиент, равна 0,16. Для второго клиента вероятность такого обращения равна 0,21. Для третьего клиента – 0,11. Найти вероятность того, что в течение года в страховую компанию обратится хотя бы один клиент, если обращения клиентов - события независимые.
Решение

Обозначим через А₁ событие, состоящее в том, что в страховую компанию обратился первый клиент; через А₂ – событие, состоящее в том, что в страховую компанию обратился второй клиент; через А₃ – событие, состоящее в том, что в страховую компанию обратился третий клиент.

Через А обозначим интересующее событие, состоящее в том, что в течение года в страховую компанию обратится хотя бы один клиент.

Вероятность наступления события А, состоящего в появлении хотя бы одного из независимых событий А₁, А₂, А₃, равна разности между единицей и произведением вероятностей противоположных событий :



Поскольку же 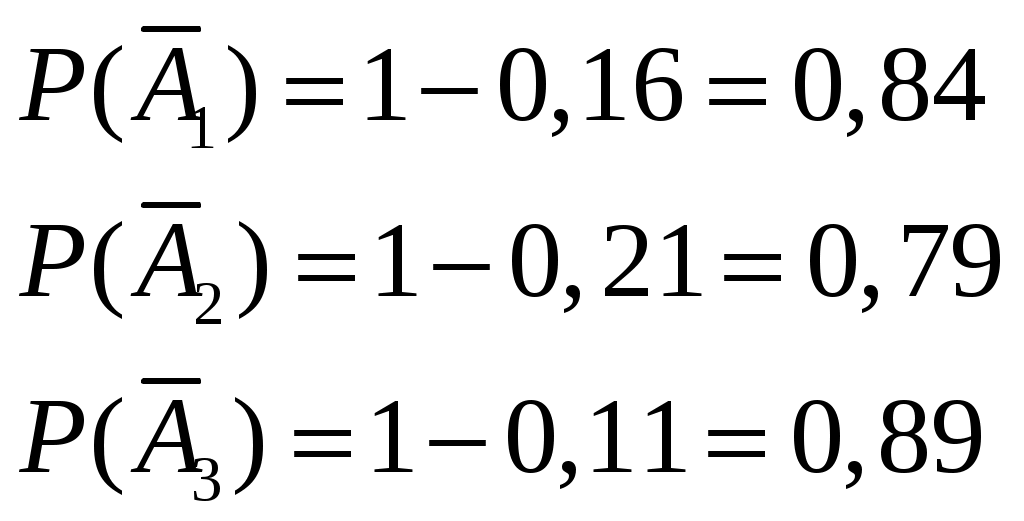и, следовательно, , имеем:



Тогда:
Ответ: вероятность того, что в течение года в страховую компанию обратится хотя бы один клиент, составляет 0,41.

Задача №3

В брокерской компании, в которой 31% составляют сотрудники первого отдела, 26% - второго, остальные третьего, результаты работы оцениваются по отдаче с каждого инвестированного сотрудником рубля (высокая или низкая). Анализ последнего месяца работы показал, что низкую отдачу имеют 2,1% сотрудников первого отдела, 1,1% - второго и 1,6% - третьего отдела. Какова вероятность того, что случайно выбранный сотрудник компании за последний месяц показал высокую отдачу? Если сотрудник показал низкую отдачу, то в каком отделе, скорее всего, он работает?
Решение

1. Какова вероятность того, что случайно выбранный сотрудник компании за последний месяц показал высокую отдачу?

Обозначим за A событие: случайно выбранный сотрудник компании за последний месяц показал высокую отдачу.

Очевидно, что возможны три варианта выбора сотрудника:

В₁ – выбран сотрудник из первого отдела;

В₂ – выбран сотрудник из второго отдела;

В₃ – выбран сотрудник из третьего отдела.

В соответствии с процентным соотношением сотрудников различных отделов в компании, вероятности выбора сотрудника соответственно равны:

,

где - вероятность того, что выбранный сотрудник окажется сотрудником первого отдела; - вероятность того, что выбранный сотрудник окажется сотрудником второго отдела; - вероятность того, что выбранный сотрудник окажется сотрудником третьего отдела.

Условная вероятность того, что выбранный сотрудник компании за последний месяц показал высокую отдачу, при условии, что он является сотрудником первого отдела, составляет: .

Условная вероятность того, что выбранный сотрудник компании за последний месяц показал высокую отдачу, при условии, что он является сотрудником второго отдела, составляет: .

Условная вероятность того, что выбранный сотрудник компании за последний месяц показал высокую отдачу, при условии, что он является сотрудником третьего отдела, составляет: .

В соответствии с формулой полной вероятности, вероятность события А, которое может наступить лишь при появлении одного из несовместимых событий (гипотез) В₁, В_2, …, В_n, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А. В данном случае:



Таким образом:



Таким образом, вероятность того, что случайно выбранный сотрудник компании за последний месяц показал высокую отдачу, составила 0,9768.
2. Если сотрудник показал низкую отдачу, то в каком отделе, скорее всего, он работает?

Обозначим через А событие, заключающееся в том, что сотрудник показал низкую отдачу. Данное событие является противоположным событию, рассмотренному в первом пункте задания, соответственно его вероятность составит:



В соответствии с формулой Бейеса, если событие А уже произошло (при этом событие А может наступить лишь при условии появления одного из несовместимых событий (гипотез) В₁, В_2, …, В_n, образующих полную группу), то вероятности гипотез могут быть переоценены по формуле:



Вероятности выбора сотрудника были определены ранее.

Условная вероятность того, что выбранный сотрудник компании за последний месяц показал низкую отдачу, при условии, что он является сотрудником первого отдела, составляет: .

Условная вероятность того, что выбранный сотрудник компании за последний месяц показал низкую отдачу, при условии, что он является сотрудником второго отдела, составляет: .

Условная вероятность того, что выбранный сотрудник компании за последний месяц показал низкую отдачу, при условии, что он является сотрудником третьего отдела, составляет: .

Определим вероятности того, что сотрудник, показавший низкую отдачу, работает соответственно в первом, втором и третьем отделах:



Таким образом, наиболее вероятно, что, если сотрудник показал низкую отдачу, он работает в первом отделе.
Ответ: вероятность того, что случайно выбранный сотрудник компании за последний месяц показал высокую отдачу, составила 0,9838; наиболее вероятно, что, если сотрудник показал низкую отдачу, он работает в третьем отделе.


Задача №4

Отдел менеджмента одного из предприятий разрабатывает новую стратегию выпуска продукции. Известно, что при определенном технологическом процессе в среднем 76% всей продукции предприятия - высшего сорта, а всего производится 210 изделий. Стратегия, разработанная отделом менеджмента, основана на том, что предприятие будет рентабельным, если выпуск продукции высшего сорта будет составлять не менее 160 изделий. Оценить критически новую стратегию выпуска продукции, определив вероятность того, что предприятие будет рентабельным.
Решение

Для ответа на поставленный вопрос воспользуемся интегральной теоремой Лапласса. В соответствии с ней, вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна , событие наступит не менее раз и не более раз, приближенно равна:



Здесь:

- функция Лапласса,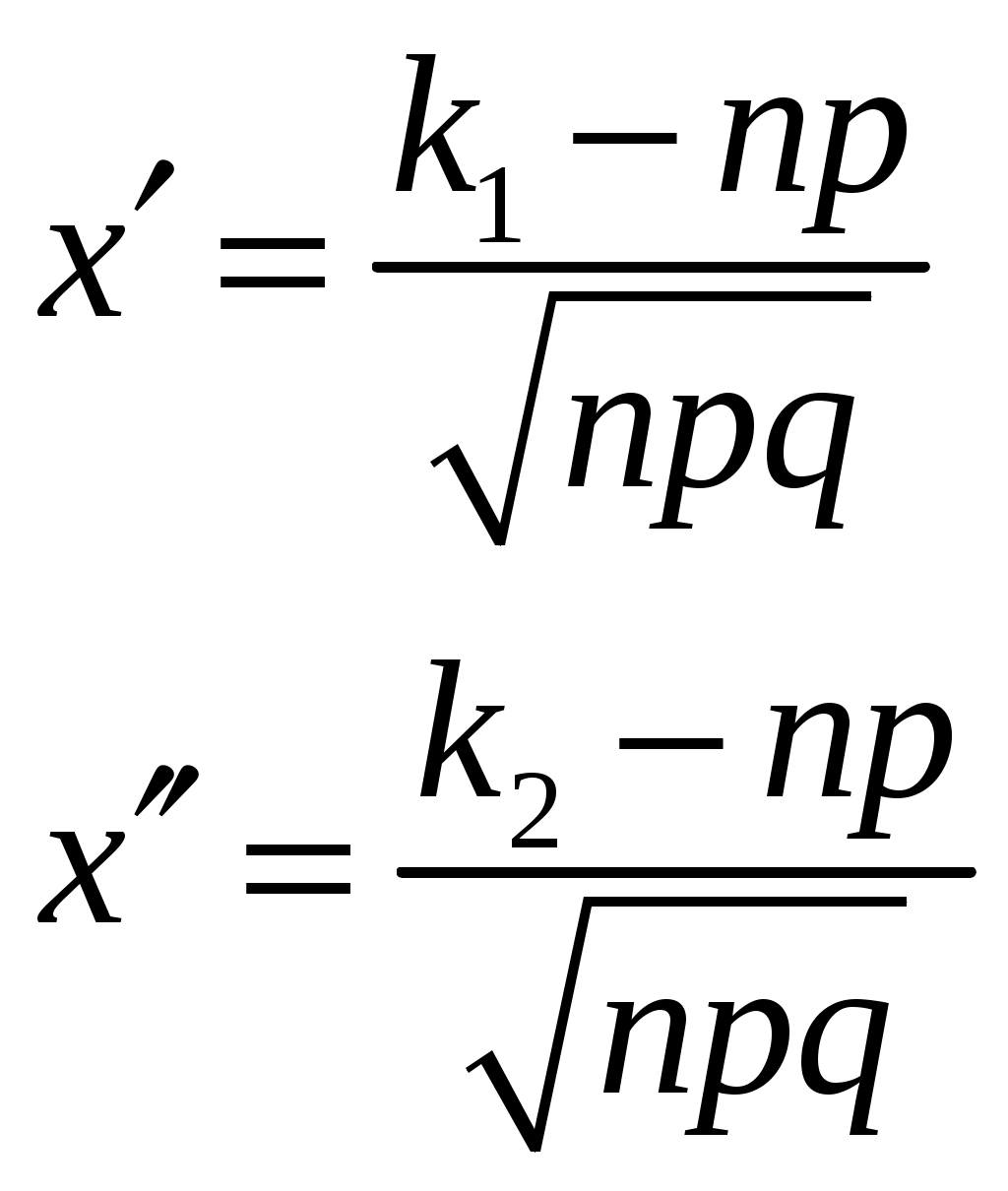



То есть:



В соответствии с исходными данными, всего производится изделий, 76% всей продукции предприятия - высшего сорта ( ). Очевидно, что продукции не высшего сорта будет произведено 100-76=24% ( ).

Требование о том, что выпуск продукции высшего сорта должен составлять не менее 160 изделий, означает, что число появлений события может быть равно 160, 161, …, 210. Соответственно принимаем:



Подставим значения в формулу:

По таблице значений функции 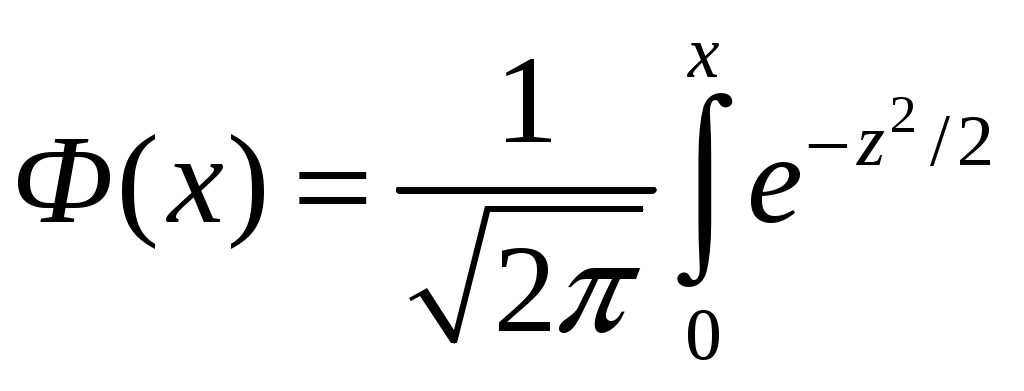находим соответствующие значения аргументов и подставляем в формулу:



Таким образом, вероятность того, что предприятие окажется рентабельным, составит всего 0,4742. Это слишком низкое значение, в связи с чем новая стратегия выпуска признается рискованной и нецелесообразной для внедрения.
Ответ: Вероятность того, что предприятие окажется рентабельным, составит всего 0,4742. Это слишком низкое значение, в связи с чем новая стратегия выпуска признается рискованной и нецелесообразной для внедрения.

Задача №5

Торговый агент в среднем контактирует с 4 потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершит покупку, равна 0,31. Составить закон распределения ежедневного числа продаж для агента. Найти числовые характеристики этого распределения. Чему равна вероятность того, что у агента будет хотя бы 2 продажи в течение дня?
Решение

Дискретная случайная величина X (число продаж агента) имеет следующие возможные значения: x₁=0 (ни один из потенциальных покупателей не совершил покупку), x₂=1 (один из потенциальных покупателей совершил покупку, то есть агентом совершена одна продажа), x₃=2 (две продажи), x₄=3 (три продажи), x₅=4 (четыре продажи).

Факты совершения продаж разным потенциальным покупателям независимы друг от друга, вероятности совершения потенциальными покупателями покупок равны между собой, поэтому применима формула Бернулли:



В данном случае:

(количество потенциальных клиентов в день);

(вероятность совершения покупки);

(вероятность того, что потенциальный покупатель не совершит покупку).

Таким образом: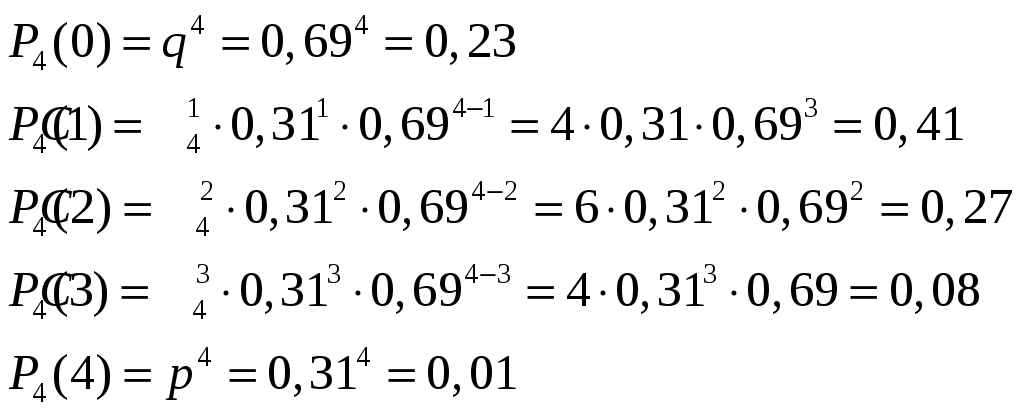



Несложно видеть, что сумма найденных вероятностей равна единице, что подтверждает правильность выполненных расчетов.

Таким образом, искомый закон распределения ежедневного числа продаж для агента будет выглядеть следующим образом:

Xi	0	1	2	3	4
pi	0,23	0,41	0,27	0,08	0,01

Найдем числовые характеристики данного распределения, рассчитав математическое ожидание, дисперсию и среднее квадратическое отклонение.

1. Математическое ожидание:





2. Дисперсия:



Для упрощения расчетов запишем закон распределения :

X2i	0	1	4	9	16
pi	0,23	0,41	0,27	0,08	0,01

Найдем математическое ожидание :



Найдем дисперсию:



3. Среднее квадратическое отклонение:




Определим вероятность того, что у агента будет хотя бы 2 продажи в течение дня. Очевидно, что данному условию удовлетворяют три события:

• 
  состоялись 2 продажи;
  
• 
  состоялись 3 продажи;
  
• 
  состоялись 4 продажи.
  

Таким образом, искомая вероятность составит:



Используя найденный ранее закон распределения ежедневного числа продаж для агента, получаем:


Ответ:

Искомый закон распределения:

Xi	0	1	2	3	4
pi	0,23	0,41	0,27	0,08	0,01

Числовые характеристики распределения:






Вероятность того, что у агента будет хотя бы 2 продажи в течение дня, составила 0,36.

Задача №6

Дискретная случайная величина Х с математическим ожиданием М(Х)=5,8 задана рядом распределения:

xi	-9	0	9	20
pi	p1	0,4	p3	0,2

а) найти р₁ и р₃;

б) построить многоугольник распределения;

в) построить интегральную функцию распределения F(x) и ее график;

г) вычислить дисперсию D(X); пояснить, как можно интерпретировать ее значение.
Решение

а) найти р₁ и р₃.

Для нахождения вероятностей р₁ и р₃ воспользуемся формулой математического ожидания и тем фактом, что сумма вероятностей должна быть равна единице: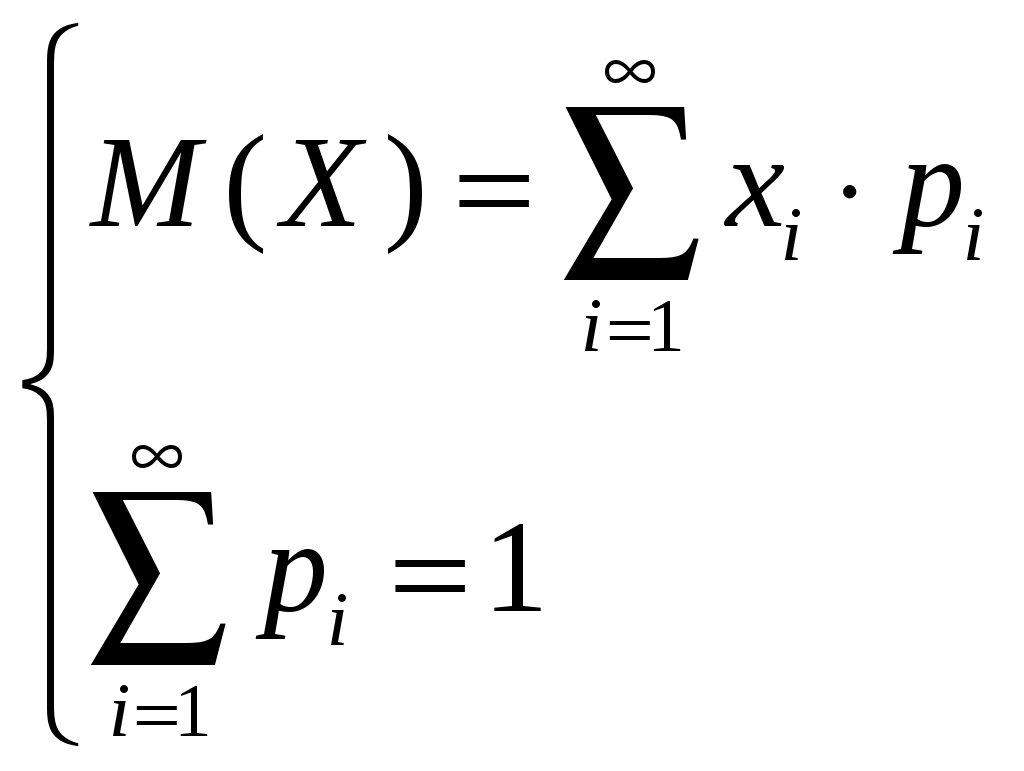



Подставим имеющиеся численные значения и решим систему уравнений:



Таким образом, ряд распределения будет выглядеть следующим образом:

xi	-9	0	9	20
pi	0,1	0,4	0,3	0,2

б) построить многоугольник распределения.

Построение многоугольника распределения осуществляется на основе информации ряда распределения. По оси абсцисс откладываются возможные значения x_i, а по оси ординат – соответствующие им вероятности p_i. Далее наносятся точки (в соответствии с рядом распределения) и соединяются между собой отрезками прямых. Построение многоугольника распределения выполнено на рисунке 6.1.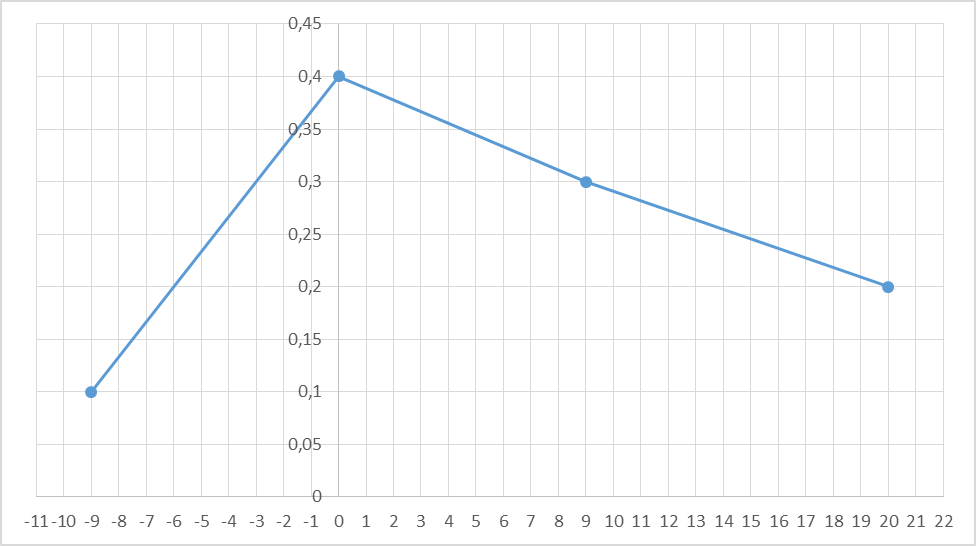



Рисунок 6.1 – Многоугольник распределения
в) построить интегральную функцию распределения F(x) и ее график.

Логика рассуждений при построении функции распределения F(x) сводится к следующему.

1. Если , то F(x)=0, поскольку значений, меньших -9, величина x не принимает.

2. Если , то F(x)=0,1 (см. ряд распределения).

3. Если , то F(x)=0,1+0,4=0,5.

4. Если , то F(x)=0,1+0,4+0,3=0,8.

5. Если , то F(x)=1, поскольку значение, превышающее 20, величина x принимает всегда.

Таким образом, функция распределения примет вид: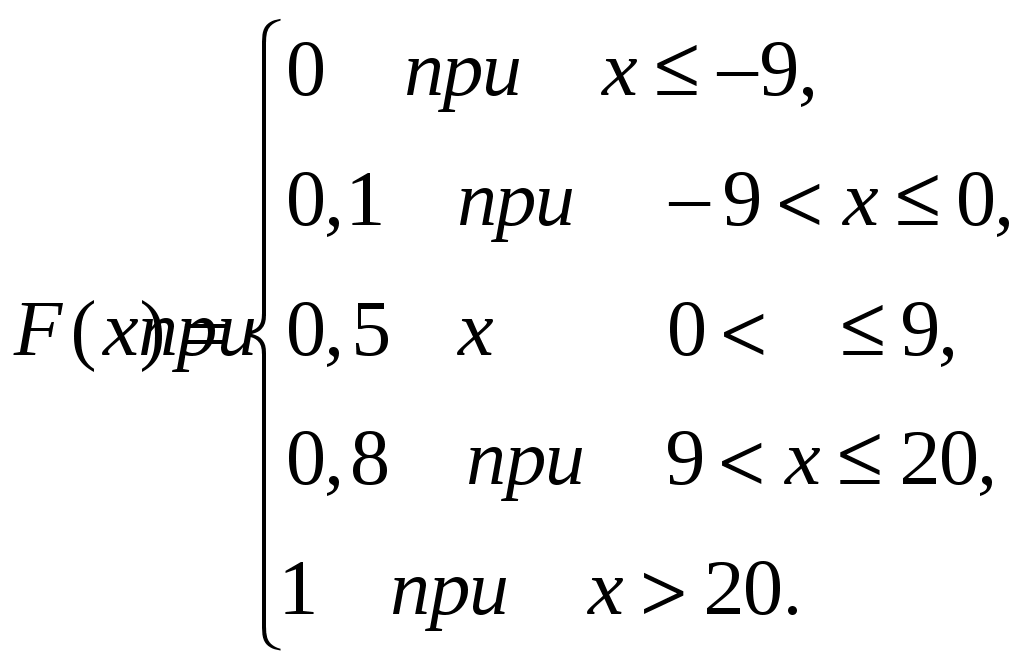



График данной функции представлен на рисунке 6.2.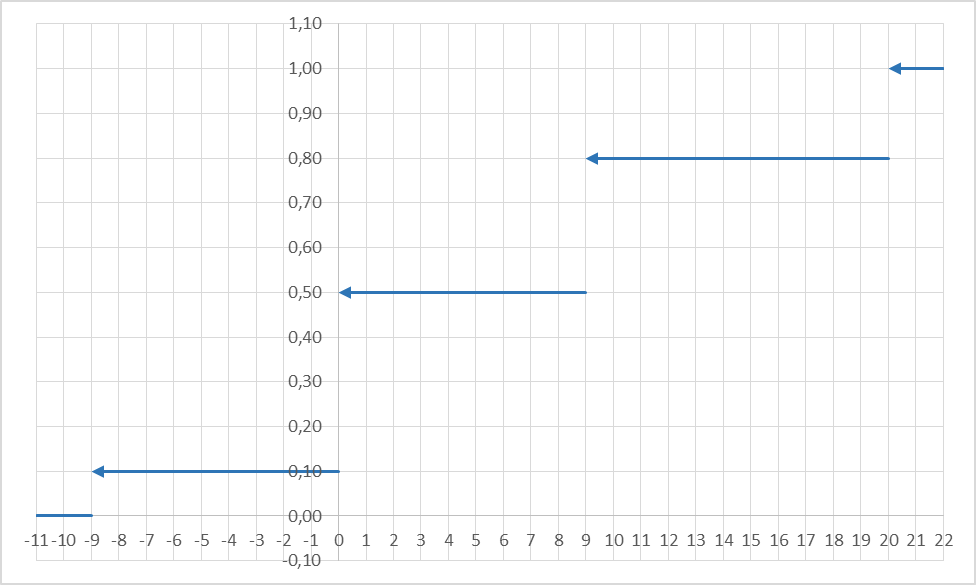



Рисунок 6.2 - График функции распределения F(x)

г) вычислить дисперсию D(X); пояснить, как можно интерпретировать ее значение.

Найдем дисперсию по формуле:



Для упрощения расчетов запишем закон распределения :

x2i	81	0	81	400
pi	0,1	0,4	0,3	0,2

Найдем математическое ожидание :



Найдем дисперсию:



В соответствии с определением, дисперсией называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Таким образом, дословная трактовка полученного значения следующая: математическое ожидание квадрата отклонения случайной величины x_i от ее математического ожидания М(Х)=5,8 составляет
Ответ:

а) р₁=0,1, р₃=0,3;

в) ;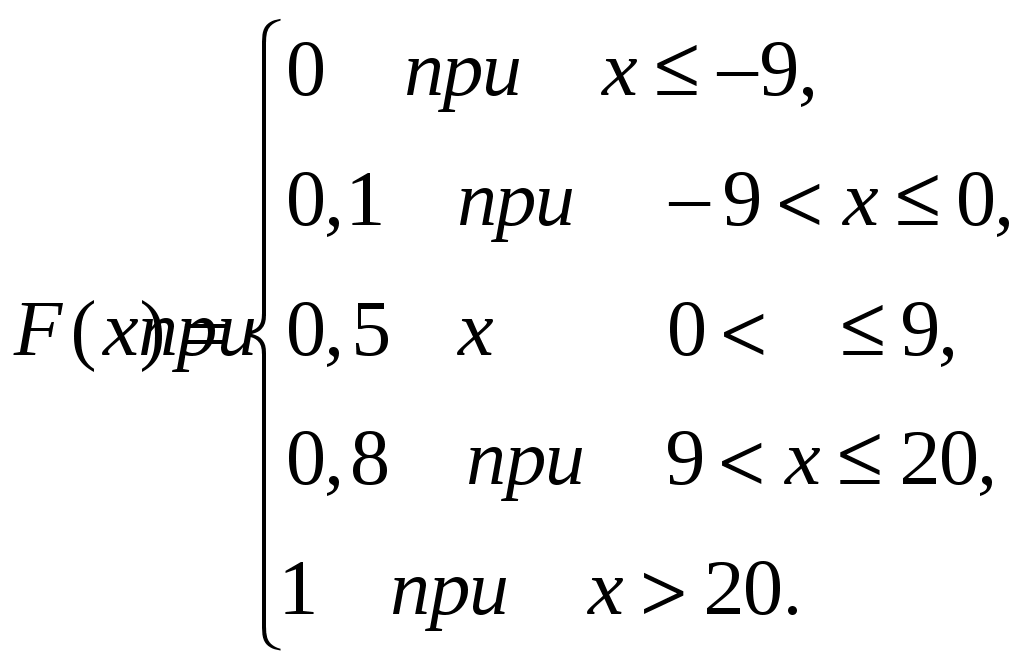

г) математическое ожидание квадрата отклонения случайной величины x_i от ее математического ожидания составляет .

Задача №7

В нормально распределенной совокупности 16% значений случайной величины X меньше 12 и 46% значений случайной величины X больше 18. Найти параметры этой совокупности.
Решение

Поскольку имеет место нормальное распределение, можно воспользоваться соотношением:

, где:

и - границы интервала;

- математическое ожидание величины X;

- среднее квадратическое отклонение величины X.
Используя исходные данные, а также таблицу значений функции 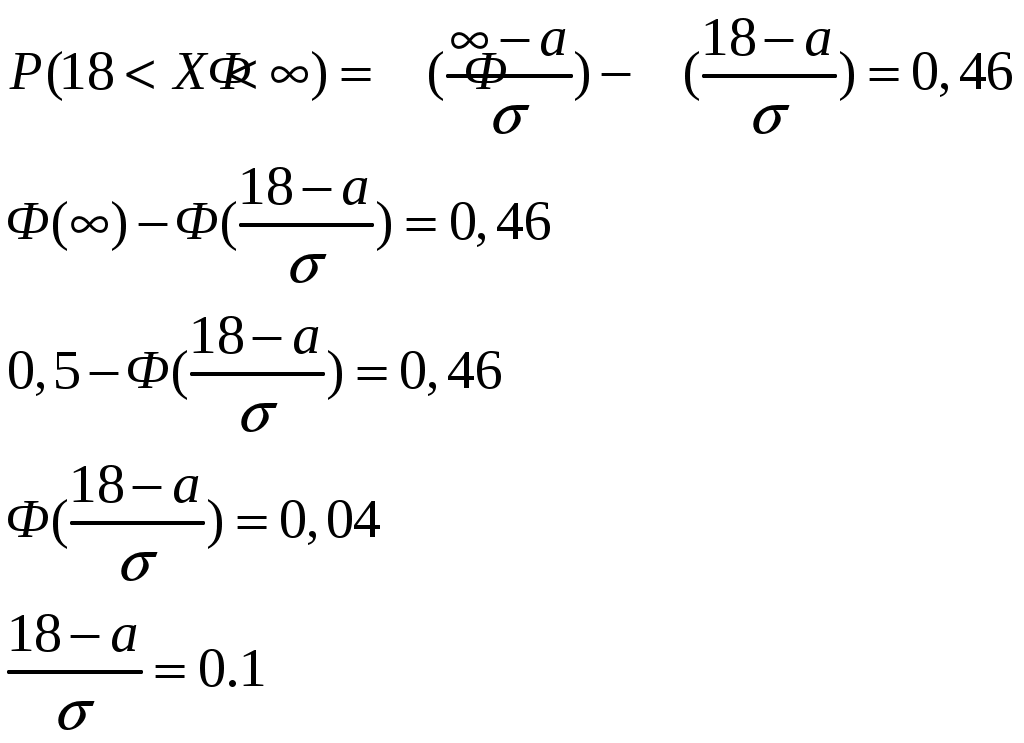, получаем:





Составим систему уравнений и решим ее:


Таким образом, математическое ожидание составило , среднее квадратическое отклонение .
Ответ: математическое ожидание составило , среднее квадратическое отклонение .

Задача №8

Прибыль от реализации инноваций в течение месяца описывается следующей функцией плотности распределения вероятностей



Найти:

а) параметр k;

б) среднюю ожидаемую прибыль;

в) интегральную функцию распределения F(x) и ее график;

г) вероятность того, что прибыль от реализации инноваций составит больше, чем 9.
Решение

а) параметр k.

Параметр k найдем из условия:



Поскольку все возможные значения случайной величины в данном случае принадлежат одному интервалу, то:



Используя исходные данные, получаем: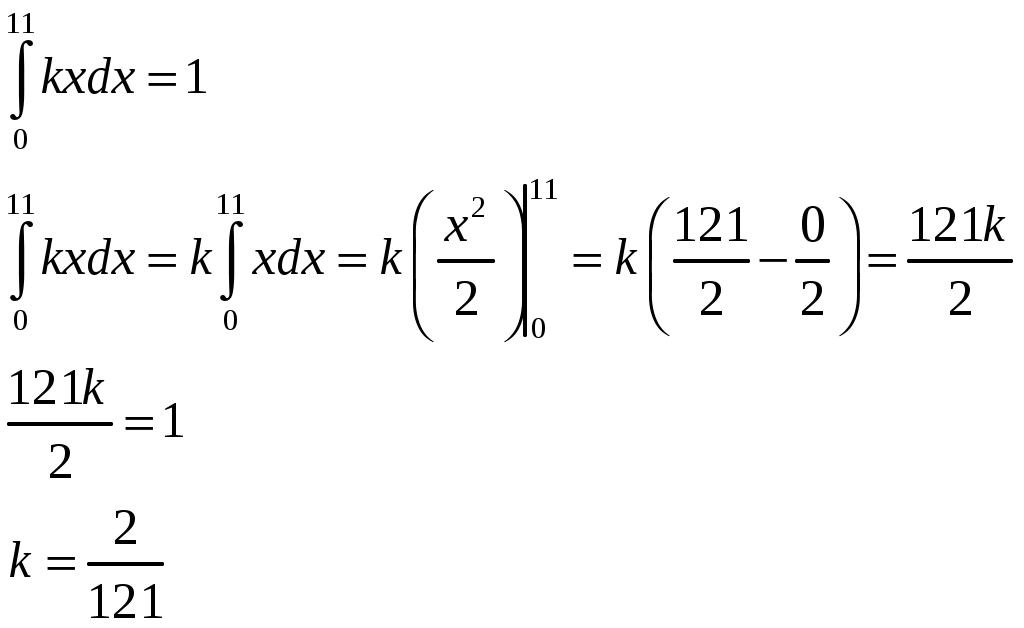



Таким образом, функцию плотности распределения вероятностей можно записать в следующем виде:


б) средняя ожидаемая прибыль.

Для ответа на вопрос воспользуемся свойством:



Поскольку все возможные значения случайной величины в данном случае принадлежат одному интервалу, то:



Используя исходные данные, получаем:



в) интегральная функция распределения F(x) и ее график.

В соответствии с определением,



Используем формулу:



В соответствии с исходными данными, если 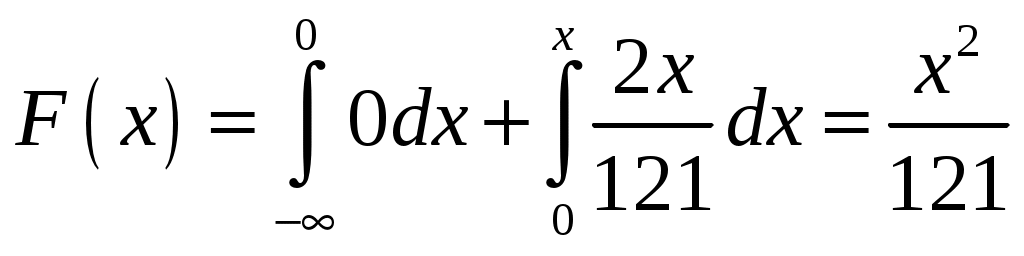, то . Следовательно:



Если 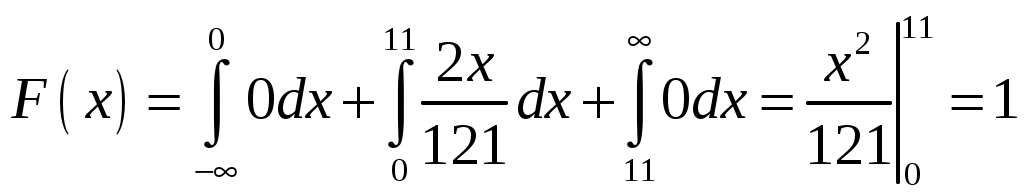, то:



Если , то:



Таким образом, искомая функция распределения примет вид:



График данной функции построен на рисунке 8.1.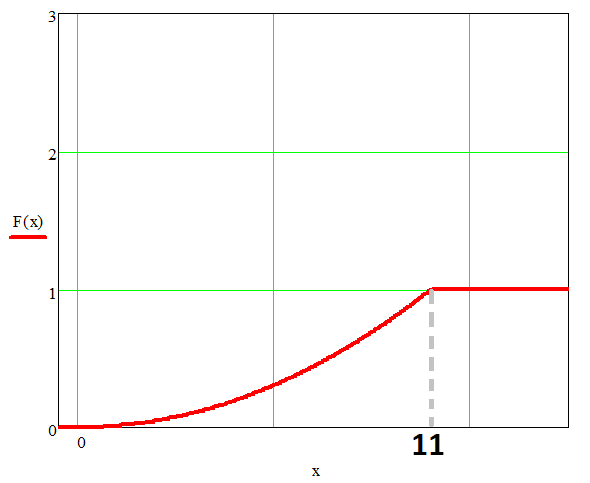



Рисунок 8.1 – График функции распределения F(x)
г) вероятность того, что прибыль от реализации инноваций составит больше, чем 9.

Используя свойство , найдем сначала вероятность того, что прибыль от реализации инноваций окажется менее 9:



Вероятность того, что прибыль от реализации инноваций составит ровно 9 единиц, согласно следствию из свойства функции распределения, равна нулю:





Очевидно, что:



Таким образом:


Ответ:

а)

б)

в)

г)
Задача №9

Случайная величина имеет биноминальное распределение с математическим ожиданием и дисперсией .

Найти Р(X  2).
Решение

В соответствии с определением, биноминальным называют закон распределения дискретной случайной величины X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p; вероятность возможного значения X=k (числа k появлений события) вычисляют по формуле Бернулли: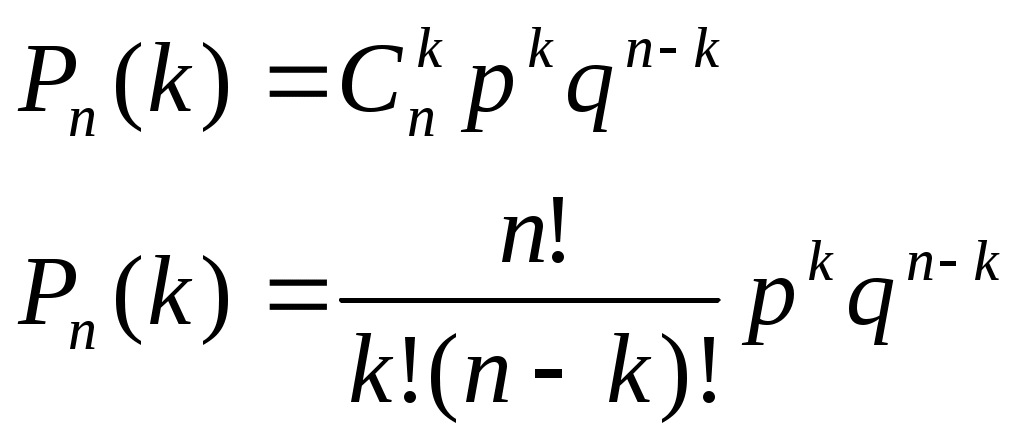



Согласно свойствам биноминального распределения:



Очевидно, что:

, то есть вероятность того, что в результате испытаний событие появится не менее двух раз (Р(X  2)) можно определить как разность между единицей и суммой вероятностей появления события 0 раз и 1 раз.

Таким образом:



Используя исходные данные, найдем необходимые числовые значения:



Подставляем полученные значения:



Ответ:
Задача №10

В среднем за час автомойку посещает п=5 клиентов. Найти вероятность того, что за два часа автомойку посетят не менее k=9 клиентов, и вероятность того, что в течение как минимум T=10 минут на автомойке не будет ни одного клиента. Число посетителей за час распределено по закону Пуассона, а время ожидания клиента распределено по показательному закону.
Решение

В соответствии с исходными данными, число посетителей за час распределено по закону Пуассона:



При этом:







Очевидно, что:



Тогда:



В соответствии с заданием, время ожидания клиента распределено по показательному закону:



Используя свойство , найдем сначала вероятность того, что на автомойке не будет ни одного клиента не дольше 10 минут:



Очевидно, что:



Тогда:


Ответ: вероятность того, что за два часа автомойку посетят не менее k=9 клиентов, составляет 0,6671, а вероятность того, что в течение как минимум T=10 минут на автомойке не будет ни одного клиента, составляет 0,4346.

Список использованных источников

1. 
   Башмакова И.Б. Теория вероятностей [Текст] : учебное пособие / И. Б. Башмакова, И. И. Кораблёва, С. С. Прасникова ; Министерство образования и науки Российской Федерации, Санкт-Петербургский государственный архитектурно-строительный университет. - Санкт-Петербург : СПбГАСУ, 2016. - 104 с.
   
2. 
   Денисова О.И. Теория вероятностей [Текст] : учебное пособие / О. И. Денисова ; М-во сельского хоз-ва Российской Федерации, Российский гос. аграрный ун-т - МСХА им. К. А. Тимирязева. - Москва : Изд-во РГАУ-МСХА, 2017. - 109 с.
   
3. 
   Кеворков В.Б. Теория вероятности [Текст] : [18+] / Ваграм Кеворков. - Москва : У Никитских ворот, 2016. - 476 с.
   
4. 
   Князева О.О. Теория вероятностей и математическая статистика [Текст] : учебное пособие : [в 2 ч.] / Князева О. О., Сосковец Л. А. ; Омский филиал негосударственного образовательного частного учреждения высшего образования "Московский финансово-промышленный университет "Синергия". - Омск : Издательский центр КАН, 2018 г.
   
5. 
   Маркова Н.А. Теория вероятностей [Текст] : учебное пособие / Н. В. Маркова ; М-во образования и науки Хабаровского края, Федеральное гос. бюджетное образовательное учреждение высш. образования "Тихоокеанский гос. ун-т". - Хабаровск : Изд-во ТОГУ, 2016. - 123 с.
   
6. 
   Плескунов М.А. Теория вероятностей [Текст]. - Екатеринбург : Издательство Уральского университета, 2017. - 134 с.
   
7. 
   Туганбаев А.А. Теория вероятностей [Текст] : учебник / А. А. Туганбаев, Е. И. Компанцева ; Национальный исследовательский университет МЭИ, Финансовый университет при правительстве Российской Федерации. - Москва : ФЛИНТА, 2018. - 180 с.