Моделирование помехоустойчивости канала связи с квадратурной амплитудной модуляции
 Скачать 123.44 Kb.
|
|
МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ ЧВВМУ им. П. С. Нахимова Курсовая работа по дисциплине: проектирование защищенных телекоммуникационных систем. Тема: «Моделирование помехоустойчивости канала связи с квадратурной амплитудной модуляции» Выполнила: студентка 758 группы Козенцова А.Р. Проверил: Иськив В.М. Севастополь 2018 Содержание Введение.
Список литературы. Введение. Квадратурная модуляция имеет большую помехоустойчивость в сравнении с многократной ОФМ. Но при увеличении числа позиций свыше 16 и ее помехоустойчивость оказывается недостаточно для качественной передачи. Поэтому во всех современных высокоскоростных протоколах КАМ используется, в совокупности с помехоустойчивым кодированием. В качестве ПУ кодирования используется один из видов сверточных кодов - решетчатый код. Такое совместное кодирование получило название «Треллис - модуляции» (ТСМ). При применении треллис - модуляции число сигнальных точек увеличивается вдвое за счет добавления к информационным битам одного избыточного, образованного путем сверточного кодирования. Треллис - модуляция обеспечивает большую помехоустойчивость. 1.Описание алгоритма. При использовании данного алгоритма передаваемый сигнал кодируется одновременными изменениями амплитуды синфазной (I) и квадратурной (Q) компонент несущего гармонического колебания (fc ), которые сдвинуты по фазе друг относительно друга на π/2. Результирующий сигнал Z формируется в результате суммирования этих колебаний. Таким образом, QAM -модулированный дискретный сигнал может быть представлен соотношением:  , гдеt - изменяется в диапазоне  ;m - порядковый номер дискрета времени;  - шаг квантования входного сигнала по времени;p - шаг квантования входного сигнала по амплитуде;  и  – модуляционные коэфициенты ( ).Этот же сигнал также может быть представлен в комплексном виде:  , или  , где: – алгоритм изменения амплитуды модулированного сигнала; – алгоритм изменения фазы модулированного сигнала.Таким образом, при использовании квадратурной амплитудной модуляции передаваемая информация кодируется одновременными изменениями амплитуды и фазы несущего колебания. На рисунке 1 представлен принцип формирования результирующего колебания Z путем суммирования вектора квадратурной составляющей Q с вектором синфазной составляющей I. 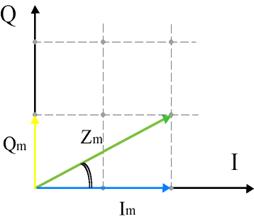 Рисунок 1 Амплитуда вектора Z определяется соотношением Am , а угол, который этот вектор образует с осью абсцисс, определяется соотношением φm . Для данного алгоритма существенно, что при модулировании синфазной и квадратурной составляющей несущего колебания используется одно и то же значение шага изменения амплитуды. Поэтому окончания векторов модулированного колебания образуют прямоугольную сетку на фазовой плоскости действительной - Re{Z} и мнимой - Im{Z} составляющих вектора модулированного сигнала. Число узлов этой сетки определяется типом используемого алгоритма QAM. Схему расположения узлов на фазовой плоскости модулированного QAM колебания принято называть созвездием (constellation). Для указания типа алгоритма QAM принята следующая схема обозначения: QAM-<число >. Используемое в обозначении алгоритма числовое значение обычно представляет собой число вида 2N и соответствует количеству узлов на фазовой сетке, а также максимальному количеству различных значений вектора модулированного сигнала. Следует отметить, что в данном случае значение N соответствует показателю спектральной эффективности алгоритма. На рисунке 2 приведена упрощенная структурная схема формирователя QAM-модулированного сигнала. 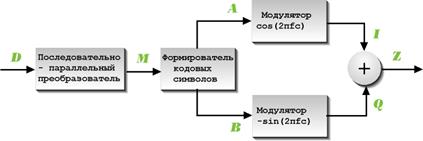 Рисунок 2 На первом этапе преобразования последовательность битов D {d0 , d1 ,...,dk } от источника сигнала преобразуется в последовательность двумерных модуляционных символов M {m0 m1 , mj }. Число битов в каждом определяется значением N (для алгоритма QAM-16 N=log2 16=4). Формирователь кодовых символов преобразует двумерный кодовый символ mj в пару кодовых символов αj и βj . Для алгоритма QAM-16 допустимые значения αj и βj принадлежат множеству {1,3,-1,-3} и определяют, соответственно, значения действительной и мнимой координаты вектора модулированного колебания. Сформированные значения А {αj } и B {βj } используются для амплитудной модуляции синфазной I и квадратурной Q составляющих несущего колебания. На последнем этапе преобразования выполняется суммирование этих колебаний и формирование результирующего сигнала Z. На рисунке 3 представлено расположение векторов модулированного колебания - созвездие для алгоритма QAM-16. 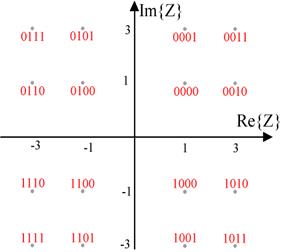 Рисунок 3 Красным цветом отмечены значения модуляционных символов, которым соответствуют указанные точки фазовой плоскости модулированного колебания {m3 , m2 ,m1 ,m0 }. Для алгоритма QAM-16 пара {m3 ,m2 } определяет номер квадранта фазовой плоскости или знаки действительной и мнимой координаты вектора модулированного колебания: 00 Sign(Re{Z})=1, Sign(Im{Z})=1 10 Sign(Re{Z})=1, Sign(Im{Z})=-1 01 Sign(Re{Z})=-1, Sign(Im{Z})=1 11 Sign(Re{Z})=-1, Sign(Im{Z})=-1 Для этого алгоритма пара {m1 ,m0 } определяет значения амплитуды реальной и мнимой координаты вектора модулированного колебания соответственно. В таблице представлены значения кодовых символов α и β, которые соответствуют значениям младших разрядов модуляционного символа {m1 ,m0 }.
Преобразование модуляционных символов в кодовые символы выполняется с применением алгоритмов Грея для помехоустойчивого кодирования данных. Так векторам модулированного колебания, которые находятся близко один от другого на фазовой плоскости, ставятся в соответствие значения кодовых символов, которые отличаются значениями только одного бита. В качестве примера могут быть рассмотрены два вектора Z=1+j и Z=1+3j, которым соответствуют кодовые символы {0,0} и {0,1}. 2.Квадратурные модуляторы и демодуляторы. Основной элемент модулятора и демодулятора – перемножитель (смеситель). 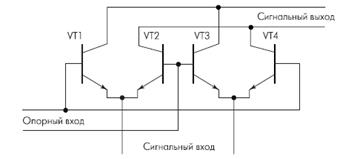 Рисунок 4 Рассматриваемый перемножитель (рис.4) представляет собой балансное устройство (double balanced Gilbert-cell mixer) на четырех транзисторах с дифференциальными входами (сигнальным и опорного колебания) и дифференциальным выходом. Для входного и выходного сигналов перемножитель представляет собой токовый элемент с низким входным (эмиттерным) и высоким выходным (коллекторным) сопротивлениями. Опорное колебание, с которым перемножается входной сигнал, подается в виде напряжения на базы транзисторов. Перемножитель используется вместе с преобразователем "напряжение–ток", включаемым на его эмиттерном входе. 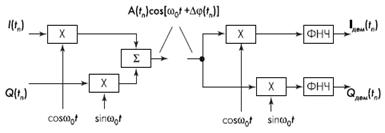 Рисунок 5 В квадратурном модуляторе (рис.5) для суммирования выходных сигналов соответствующие коллекторные выводы двух перемножителей соединяются. При подаче на входы перемножителя сигнала, в общем случае выражаемого как  , (1)где  и  – модулированные амплитуда и изменение фазы, и опорного колебания  с его выхода снимается сумма двух колебаний – с суммарной и разностной частотами:  , (2)где  пропорционально . Нужное колебание выделяется путем фильтрации или без фильтрации – в квадратурных преобразователях. Первая составляющая, с суммарной частотой  , выделяется в повышающих преобразователях частоты, а вторая, с разностной частотой  , – в понижающих преобразователях (при  ). При  вторая составляющая в выражении (2) равна  . В модуляторах реализуется режим с  (при  ), а в демодуляторах используется составляющая разностной частоты, равной нулю (при  ). Основные режимы квадратурных модулятора и демодулятора (см. рис.5) – модуляция/демодуляция сигнала с синфазной I(tn ) и квадратурной Q(tn ) модулирующими посылками и модуляция/демодуляция аналогового сигнала с одной боковой полосой (ОБП, SSB). В первом режиме модулирующие посылки – аналоговые, с постоянным уровнем в течение каждой посылки и дискретным изменением уровней от посылки к посылке. Уровни содержат информацию о цифровом коде модулирующего сигнала. На выходе модулятора , (3)где  и  – дискретно изменяемые амплитуда и фаза модулированного сигнала. Сигналы на выходе демодулятора (4) (5)пропорциональны входным сигналам модулятора I(tn ) и Q(tn ). Отметим, что НЧ-составляющие I(tn ), Q(tn ) на входе модулятора и Iдем (tn ), Qдем (tn ) на выходе демодулятора представляют сигнал в прямоугольной системе, тогда как сигнал на выходе модулятора и входе демодулятора, согласно выражению (3), – в полярной системе координат. Во втором режиме на квадратурные входы модулятора подаются "комплексные" составляющие модулирующего НЧ-сигнала (со сдвигом 90°). С выхода модулятора, в зависимости от знака суммирования, снимается один из двух модулированных сигналов:  (6)или  , (7)содержащих верхнюю или нижнюю боковые полосы (без инверсии и с инверсией спектра, соответственно). В выражениях (6) и (7)  и  – амплитуды и изменения фазы спектральных составляющих модулирующего сигнала. Пример аналоговых квадратурных модуляторов/демодуляторов – микросхемы серии AD834x фирмы Analog Devices (модуляторы AD8345/6/9 и демодуляторы AD8347/8). Модуляторы могут быть использованы также в качестве повышающих бесфильтровых преобразователей частоты. Другая серия аналоговых микросхем – AD607 и ее вариант AD61009. Это – микросхемы подсистем приемного тракта, содержащих понижающий преобразователь частоты и квадратурный демодулятор.3.Помехоустойчивость алгоритма КАМ. Помехоустойчивость ал горитма QAM обратно пропорциональна его спектральной эффектив ности. Воздействие помех приводит к возникнове нию неконтролируемых изменений амплитуды и фазы передаваемого по линии сигнала. При уве личении числа кодовых точек на фазовой плоско сти расстояние между ними (P) уменьшается и, следовательно, возрастает вероятность ошибок при распознавании вектора Zm * на приемной стороне. Предельный уровень допустимых амплитудных и фазовых искажений QAM-модулированного сигнала представляет собой круг диаметром P (рис. 10). 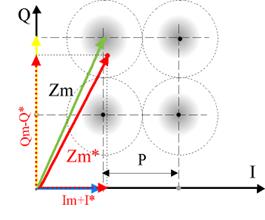 Рисунок 10 Центр этого круга совпадает с узлом квадратурной сетки на фазовой плоскости. Заштрихованные области на рисунке соответствуют координатам искаженного вектора QAM-модулированного ко лебания при воздействии на полезный сигнал помехи, относительный уровень которой опре деляется соотношением 20dB £ SNR £30dB. На диаграмме, которая приведена на рисунке 11, сплошными линиями представлены зависимости ожидаемого значения BER (Bit Error Rate - вероятность ошибок) от величины SNR для различных вариантов алгоритма QAM. 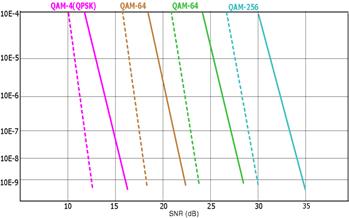 Использование дополнительного кодирования (пунктирные линии), например, по алгоритму Рида-Соломона (Reed-Solomon) позволяет повысить помехоустойчивость модулированного сигнала. Достоинства алгоритма: Алгоритм квадратурной амплитудной модуляции является относительно простым в реализации и в то же время достаточно эффективным алгоритмом линейного кодирования xDSL-сигналов. Современные реализации этого алгоритма обеспечивают достаточно высокие показатели спектральной эффективности. Как уже было отмечено выше, ограниченность спектра и относительно высокий уровень помехоустойчивости QAM-модулированного сигнала обеспечивают возможность построения на основе этой технологии высокоскоростных ADSL и VDSL-систем передачи данных по двухпроводной линии с частотным разделением принимаемого и передаваемого информационных потоков. Недостатки алгоритма: К недостаткам алгоритма можно отнести относительно невысокий уровень полезного сигнала в спектре модулированного колебания. Этот недостаток является общим для алгоритмов гармонической амплитудной модуляции и выражается в том, что максимальную амплитуду в спектре модулированного колебания имеет гармоника с частотой несущего колебания. Поэтому данный алгоритм в чистом виде достаточно редко используется на практике. Гораздо более широкое распространение получают алгоритмы, которые используют основные принципы QAM и в то же время свободны от его недостатков (например - алгоритм CAP). Список литературы. 1. ФилимоновА.. Алгоритмы модуляции протоколов XDSL. http://www.protocols.ru/files/Technologies/xDSL.pdf 2. Голуб В. Квадратурные модуляторы и демодуляторы в системах радиосвязи. http://www.electronics.ru/pdf/3_2003/06.pdf 3. Пасковатый А. Модемные протоколы физического уровня. http://www.analytic.ru/ftproot/pub/byb_art/physics.zip 4. Пахомов С. Технология 1000Base-T на физическом уровне. http://www.compress.ru/article.aspx?id=9774&iid=412 |