Прак_03. Модульная арифметика. Операция по инверсии
 Скачать 183 Kb. Скачать 183 Kb.
|
|
Практическая работа №3. ТЕМА: МОДУЛЬНАЯ АРИФМЕТИКА. ОПЕРАЦИЯ ПО ИНВЕРСИИ. Цель работы: Операция по модулу. Найдите мультипликативные инверсии b в Zn и создайте программа для алгоритм на программированных язиках. Теоретический часть. Известно, что   два входяший и два выходяшие значение. два входяший и два выходяшие значение.Нам интиресует только остаток  , другими словами если Мы делим а на , другими словами если Мы делим а на 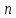 остаётся остаток остаётся остаток  . Это называется бинарной операции и обозначается по модулю . Это называется бинарной операции и обозначается по модулю 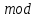 . Второй входяший делитель . Второй входяший делитель 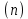 называются модул. Выходяший значения называются модул. Выходяший значения  называются остаток. Қуйидаги расмда модул арифметикаси ва қолдиқли бўлиш тенгламаси келтирилган. называются остаток. Қуйидаги расмда модул арифметикаси ва қолдиқли бўлиш тенгламаси келтирилган. 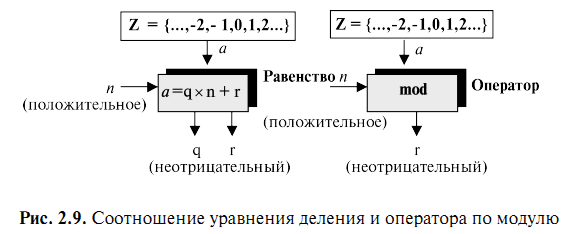 Операции по модулю Вышеупомянутый бинарный оператор назван оператором по модулю и обозначается как mod. Второй вход ( n ) назван модулем. Вывод r назван вычетом. Рисунок 2.9 показывает отношение деления по сравнению с оператором по модулю.  Соотношение уравнения деления и оператора по модулю Как показано на рис. 2.9, оператор по модулю ( mod ) выбирает целое число ( a ) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ). Мы можем сказать, что  Мы уже упоминали, что два входа для трех бинарных операторов в сравнении по модулю могут использовать данные из Z или Zn. Следующие свойства позволяют нам сначала отображать два входа к Zn (если они прибывают от Z ) перед выполнением этих трех бинарных операторов Заинтересованные читатели могут найти доказательства для этих свойств в приложении Q. 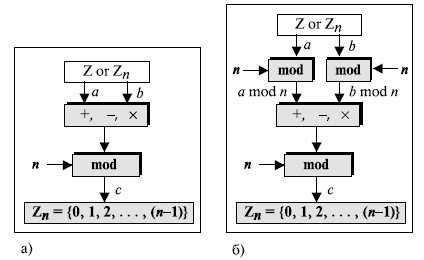 Рис. 2.14. Свойства оператора mod  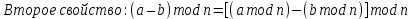 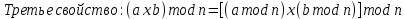 Аддитивная инверсия. В Zn два числа a и b аддитивно инверсны друг другу, если 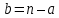 . Например, . Например, В Zn аддитивная инверсия числу a может быть вычислена как b = n – a. Например, аддитивная инверсия 4 в Z10равна 10 – 4 = 6. В модульной арифметике каждое целое число имеет аддитивную инверсию. Сумма целого числа и его аддитивной инверсии сравнима с 0 по модулю n. Мультипликативная инверсия. В Zn два числа a и b мультипликативно инверсны друг другу, если Например, если модуль равен 10, то мультипликативная инверсия 3 есть 7. Другими словами, мы имеем В модульной арифметике целое число может или не может иметь мультипликативную инверсию. Целое число и его мультипликативная инверсия сравнимы с 1 по модулю n . Может быть доказано, что a имеет мультипликативную инверсию в Zn, если только НОД(n, a) = 1. В этом случае говорят, что a и n взаимно простые. Расширенный алгоритм Евклида находит мультипликативные инверсии b в Zn , когда даны n и b и НОД (n, b) = 1 . Мультипликативная инверсия b — это значение t , отображенное в Zn .  1-занятия. Найти результат следующих операций: a. 27 mod 5 b. 36 mod 12 c. –18 mod 14 d. –7 mod 10 Решение. Мы ищем вычет r. Мы можем разделить a на n и найти q и r. Далее можно игнорировать q и сохранить r. а. Разделим 27 на 5 - результат: r = 2. Это означает, что 27 mod 5 = 2. б. Разделим 36 на 12 — результат: r = 0. Это означает, что 36 mod 12 = 0. в. Разделим (–18) на 14 — результат: r = –4. Однако мы должны прибавить модуль (14), чтобы сделать остаток неотрицательным. Мы имеем r = –4 + 14 = 10. Это означает, что –18 mod 14 = 10. г. Разделим (–7) на 10 — результат: r = –7. После добавления модуля –7 мы имеем r = 3. Это означает, что –7 mod 10 = 3. 2- занятия. Выполните следующие операции (поступающие от Zn ): a. Сложение 17 и 27 в Z14 b. Вычитание 43 из 12 в Z13 c. Умножение 123 на -10 в Z19 Решение. Ниже показаны два шага для каждой операции: (17 + 27) mod 14 -> (44) mod 14 = 2 (12 – 43) mod 13 -> (–31) mod 13 = 8 ((123) x (–10)) mod 19 -> (–1230) mod 19 = 5 3- занятия. Найдите все взаимно обратные пары по сложению в Z10. Решение. Даны шесть пар аддитивных инверсий — (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). В этом списке 0 — инверсия самому себе; так же и 5. Обратите внимание: аддитивные инверсии обратны друг другу; если 4 — аддитивная инверсия 6, тогда 6 — также аддитивная инверсия числу 4 4- Занятия. Найти все мультипликативные обратные пары в Z11. Решение. Мы имеем следующие пары: (1, 1), (2, 6), (3, 4), (5, 9), (7, 8) и (10, 10). При переходе от Z10 к Z11число пар увеличивается. При Z11 НОД (11, a) = 1 (взаимно простые) для всех значений a, кроме 0. Это означает, что все целые числа от 1 до 10 имеют мультипликативные инверсии. 5-Занятия. Реализуем алгоритм инверсия по модулу Включаем программа Visual studio 2013 создаем файл по имени “тескари” на язиках c#  В главный окно набираем следившем кодом. using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Teskari_sonni_topish { class Program { static void Main(string[] args) { // Multipliktiv teskari sonni topish. Muallif Umidjon.15.03.2017 nishon: Console.WriteLine("Songa multiplikativ teskari sonni topish"); int r1, r2, r, t1, t2, t, q, a, b,n; Console.Write("sonni kiriting b= "); b = int.Parse(Console.ReadLine()); Console.Write("modulni kiriting n= "); n = int.Parse(Console.ReadLine()); //////////////////////////////////////////////////// r1 = n; r2 = b; //initalizatsiya t1 = 0; t2 = 1; while (r2 > 0) { ///////////////////////////////////////// q = r1 / r2; // r ni aniqlash r = r1 - q * r2; r1 = r2; r2 = r; ///////////////////////////////////////// t = t1 - t2 * q; t1 = t2; t2 = t; } // tublikka tekshirish if (r1 == 1) { if (t1 >= 0) { a = t1; } else { a = n + t1; } Console.WriteLine("Chekli " + n + " maydonda " + b + " soniga teskari son " + a + " ga teng."); } else { Console.WriteLine("BERILGAN SONGA BERILGAN MODUL BO'YICHA TESKARI SON YO`Q"); } Console.WriteLine(); goto nishon; Console.ReadKey(); } } } Задачи. Вычислите следушие операции. 22 mod7 5. 140mod10 -78mod13 6. 0 mod15 138 mod26 7. 27 mod26 2785 mod256 8. 250mod256 Найдите всех мултипликативных инверсия на целих чисели по модулу 20, 15, 15 и 19. Найдите всех аддитивный инверсия на целих чисели по модулу 20, 15, 15 и 19. С помошю расширенный алгоритм Евклида найдите инверсия на целих чисели 7, 8, 13, 14,24 и 33 по модулу 39. Создайте программа для алгоритм найти мултипликативных инверсия на числах на c++ или любое программный языках. |
