ИЗУЧЕНИЕ ЦЕНТРАЛЬНОГО УДАРА ШАРОВ. Литвинов 1.4. О лабораторной работе 4 Изучение центрального удара шаров
 Скачать 68.05 Kb. Скачать 68.05 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| № | Наименование прибора | Пределы измерений | Погрешность |
| 1 | Линейка | 20 см | ±0,05 см |
| 2 | Миллисекундомер | 0-99,999 с | ±0,0005 с |
| 3 | Устройство для подвески шаров и отсчета угла их отклонения | 0-45 градусов | ± 0,5 градуса |
Принадлежности и материалы: два металлических шара, линейка, весы.
Краткое теоретическое введение
Столкновением в широком смысле называется взаимодействие тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени ( 10-4 - 10-5 с).
Столкновение, при котором имеет место соприкосновение взаимодействующих тел, называется ударом. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс.

Проанализируем превращения энергии в процессе удара. Для этого процесс соударения можно разделить на две фазы. Первая фаза начинается с момента соприкосновения точек А и В шаров (рис. 1.4.1).
К концу первой фазы сближение шаров прекращается, а часть их кинетической энергии переходит в потенциальную энергию деформации. Во второй фазе происходит обратный переход потенциальной энергии упругой деформации в кинетическую энергию шаров.
При этом шары начинают расходиться. Для абсолютно упругих тел механическая энергия к концу удара восстановилась бы полностью. Удар абсолютно неупругих тел закончился бы на первой фазе. При ударе реальных тел механическая энергия к концу удара восстанавливается лишь частично вследствие потери энергии на образование остаточных деформаций, звуковые колебания, нагревание тел и др. Для учета этих потерь вводится коэффициент восстановления k , который зависит только от физических свойств материалов тел:

Часто при рассмотрении ударов главный интерес заключается не в изучении самого процесса удара, а его результата. В этом случае могут быть использованы законы сохранения импульса и энергии, которые устанавливают связь между характеристиками взаимодействующих тел до удара с характеристиками после удара.
Запишем закон сохранения импульса для рассматриваемой системы шаров
(рис. 1.4.1):
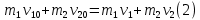
Решая совместно уравнения (1) и (2), получим выражения, связывающие скорости шаров после удара с их скоростями до удара:


Положительный результат проверки будет означать справедливость закона сохранения импульса. Кинетическая энергия системы шаров до удара больше их кинетической энергии после удара и их разница определяет потерянную за время удара кинетическую энергию системы Q:

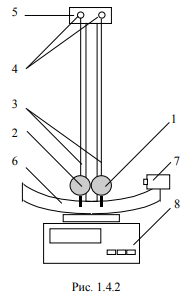 Описание экспериментальной установки
Описание экспериментальной установкиДля экспериментального изучения центрального удара шаров используется установка, представленная на рис. 1.4.2. Она представляет собой систему двух шаров 1 и 2, подвешенных к штангам 4 на токоведущих бифилярных (двойных) подвесах 3. Межцентровое расстояние шаров регулируется за счет перемещения левой штанги винтовым механизмом 5. В отрегулированном состоянии шары должны касаться друг друга в покое, при этом бифилярные подвесы - параллельны друг другу.
Результаты измерений
| № измер | Прямые измерения | Косвенные измерения | Примечание | |||||||
 |  |  |  ,м/с ,м/с | 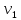 ,м/с ,м/с | 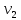 ,м/с ,м/с | 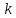 | Q, дж |    | ||
| 1 | 15 | 2,2 | 11,2 | 0,515 | 0,076 | 0,384 | 0,598 | 0,00285 | ||
| 2 | 15 | 2 | 11,9 | 0,515 | 0,069 | 0,408 | 0,658 |  | ||
| 3 | 15 | 2,1 | 10,9 | 0,515 | 0,072 | 0,374 | 0,586 | 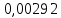 | ||
| 4 | 15 | 2,4 | 11,4 | 0,515 | 0,082 | 0,391 | 0,6 | 0,00284 | ||
| 5 | 15 | 2,2 | 11,6 | 0,515 | 0,076 | 0,4 | 0,629 | 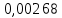 | ||
| Среднее значение | 0,515 | 0,075 | 0,391 | 0,614 | 0,00286 | |||||
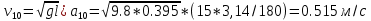


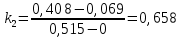



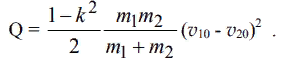





Оценка погрешностей
1) Найдём среднеарифметическое значение отдельных измерений по формуле
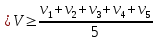

Укажем интервал значений измеряемой величины v = ± ∆v, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины.
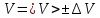
Рассчитаем отклонения от среднеарифметического каждого значения измеряемой величины:
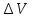 1=
1= 1;
1;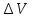 1=
1=  0,076
0,076 = -0,001
= -0,001
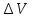 2=
2= 2;
2;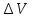 2=
2=  0,069
0,069 = -0,006
= -0,006
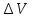 3=
3= 3;
3;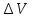 3=
3=  0,072
0,072 = 0,003
= 0,003
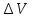 4=
4= 4;
4;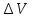 4=
4=  0,082
0,082 = -0,007
= -0,007
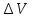 5=
5= 5
5 5=
5=  0,076
0,076 = -0,001
= -0,001
Рассчитаем среднеквадратичную погрешность результатов измерений по формуле:
 =
=
 =
=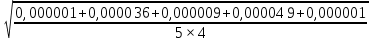 = 0,0022
= 0,0022
Рассчитаем полуширину доверительного интервала по формуле:


| № п.п. |  | <  > > |  |  |  |  |
| 1 | 0,076 | 0,075 | -0,001 |  | 0,0022 | 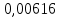 |
| 2 | 0,069 | -0,006 |  | |||
| 3 | 0,072 | 0,003 |  | |||
| 4 | 0,082 | -0,007 | 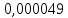 | |||
| 5 | 0,076 | -0,001 |  |


2) Найдём среднеарифметическое значение отдельных измерений по формуле
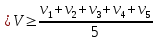

Укажем интервал значений измеряемой величины v = ± ∆v, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины.
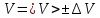
Рассчитаем отклонения от среднеарифметического каждого значения измеряемой величины:
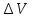 1=
1= 1;
1;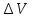 1=
1= 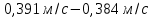 = 0,007
= 0,007
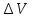 2=
2= 2;
2;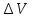 2=
2=  = -0,017
= -0,017
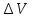 3=
3= 3;
3;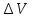 3=
3= 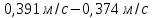 = 0,0
= 0,0
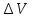 4=
4= 4;
4;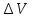 4=
4=  = 0
= 0
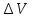 5=
5= 5
5 5 =
5 =  = -0,009
= -0,009
Рассчитаем среднеквадратичную погрешность результатов измерений по формуле:
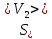 =
=
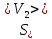 =
= = 0,00594
= 0,00594
Рассчитаем полуширину доверительного интервала по формуле:


| № п.п. |  | < 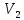 > > |  | 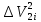 | 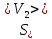 |  |
| 1 | 0,384 | 0,391 | 0,007 | 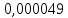 | 0,00594 |  |
| 2 | 0,408 | -0,017 |  | |||
| 3 | 0,374 | 0,0  |  | |||
| 4 | 0,391 | 0 | 0 | |||
| 5 | 0,4 | -0,009 |  |


Вывод: в результате проведения лабораторной работы мы проверили на практике выполнение закона сохранения импульса. Погрешности довольно малы.V1и V2 входят в доверительный интервал, что доказывает справедливость закона сохранения импульса.
