Логарифм. Обозначение logab Произносится логарифм b по основанию a. Из определения следует, что нахождение х log
 Скачать 181.24 Kb. Скачать 181.24 Kb.
|
|
Логарифм. Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. Обозначение: logab Произносится: «логарифм b по основанию a». Из определения следует, что нахождение х= logab равносильно решению уравнения aх=b. Пример: log28=3, потому что 23=8 Свойства логарифмов: 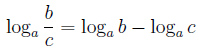 - логарифм частного - логарифм частного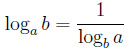 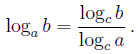 Основное логарифмическое тождество: Логарифм произведения – это сумма логарифмов: Логарифм частного — это разность логарифмов: 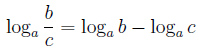 Свойства степени логарифмируемого числа и основания логарифма: Показатель степени логарифмируемого числа: Показатель степени основания логарифма: Пример: Переход к новому основанию: 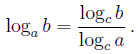 , в частности если с=b, то logbb = 1. , в частности если с=b, то logbb = 1.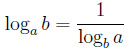 Пример: Степень логарифма: Loga (хp) = p*loga (х) Пример: log264=log2(26) = 6log22 = 6.  |
