Обратные тригонометрические функции. Обратные тригонометрические функции
 Скачать 66.6 Kb.
|
|
Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям. К ним обычно относят 6 функций: арксинус (обозначение: arcsin x; arcsin x — это угол, sin которого равен x), арккосинус (обозначение: arccos x; arccos x — это угол, косинус которого равняется x и так далее), арктангенс (обозначение: arctg x или arctan x), арккотангенс (обозначение: arcctg x или arccot x или arccotan x), арксеканс (обозначение: arcsec x), арккосеканс (обозначение: arccosec x или arccsc x). Арксинус (y = arcsin x) – обратная функция к sin (x = sin y), которая имеет область определения  и множество значений  . Другими словами возвращает угол по значению его sin.Арккосинус (y = arccos x) – обратная функция к cos (x = cos y), которая имеет область определения и множество значений  . Другими словами возвращает угол по значению его cos.Арктангенс (y = arctg x) – обратная функция к tg (x = tg y), которая имеет область определения  и множество значений  . Другими словами возвращает угол по значению его tg.Арккотангенс (y = arcctg x) – обратная функция к ctg (x = ctg y), которая имеет область определения и множество значений  . Другими словами возвращает угол по значению его ctg.arcsec - арксеканс, возвращает угол по значению его секанса. arccosec - арккосеканс, возвращает угол по значению его косеканса. Когда обратная тригонометрическая функция не определяется в указанной точке, значит, ее значение не появится в итоговой таблице. Функции arcsec и arccosec не определяются на отрезке (-1,1), а arcsin и arccos определяются только на отрезке [-1,1]. Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции прибавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции связывают с длиной дуги единичной окружности (либо углом, который стягивает эту дугу), которая соответствует тому либо другому отрезку. Иногда в зарубежной литературе, как и в научных/инженерных калькуляторах, используют обозначениями вроде sin−1, cos−1 для арксинуса, арккосинуса и тому подобное, — это считается не полностью точным, т.к. вероятна путаница с возведением функции в степень −1 («−1» (минус первая степень) определяет функцию x = f-1(y), обратную функции y = f (x)). Арксинус (обозначается как arcsin x; arcsin x — это угол, sin его равняется x). Арксинус (y = arcsin x) – обратная тригонометрическая функция к sin (x = sin y), которая имеет область определения  и множество значений . Другими словами возвращает угол по значению его sin.Функция y=sin x непрерывна и ограничена на всей своей числовой прямой. Функция y=arcsin x - строго возрастает.  Свойства функции arcsin . arcsin (-x) = - arcsin x функция нечетна, arcsin x > 0 при 0 < x ≤ 1, arcsin x = 0 при х=0, arcsin x > 0 при -1 ≤ х < 0, 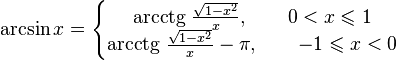 , , .График арксинуса.  Получение функции arcsin . Есть функция y = sin x. На всей своей области определения она кусочно-монотонная, таким образом, обратное соответствие y = arcsin x не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает каждое значение области значений —  . Т.к. для функции y = sin x на интервале все значения функции получается при только одном значении аргумента, значит, на этом отрезке есть обратная функция y = arcsin x, у которой график является симметричным графику функции y = sin x на отрезке относительно прямой y = x. |