обзор методов СА БФ. Обзор методов спектрального анализа булевых функций

• Название: Обзор методов спектрального анализа булевых функций
• Дата: 29.09.2022
• Размер: 0.64 Mb.
• Имя файла: обзор методов СА БФ.doc
• Тип: Обзор; #705615
• страница: 1 из 2

Обзор методов спектрального анализа булевых функций


Содержание

Введение 3

1.Основные теоретические положения 5

1.1.Спектральное представление булевых функций 6

1.2. Характеристики булевых функций 10

2.Применение спектрального анализа булевых функций 13

2.1.Анализ и синтез дискретных устройств 13

2.2.Криптография 18

2.3. Примеры применения спектрального анализа 20

Выводы 23

Список литературы 25

Введение

Спектральный анализ широко используется в математике, информатике, технике. Примером служат обработка сигналов, сжатие данных, быстрое умножение многочленов, квантовые вычисления, и т. д. Сигнал или функция представляются в виде суммы периодических функций, таких как , или (в вещественном случае) синусов и косинусов.

При исследовании булевых функций, однако, более естественным будет использование преобразования в каком-либо кусочно-постоянном базисе. Возможность характеризовать булевы функции (БФ) с помощью некоторого набора вещественных чисел впервые была отмечена в работе [1]. Впоследствии в [2] булевы функции представлялись в виде конечных сумм функций Уолша в задачах синтеза логических сетей на пороговых элементах.

За последние три десятилетия такой подход стал одним из самых важных и универсальных инструментов для ученых-теоретиков в области компьютерных вычислений и исследований.

Есть немало проблем, в анализе, проектировании, тестировании и диагностике цифровых устройств, которые намного легче решить, если логические функции, описывающие эти устройства будут представлены в спектральной области. Зачастую переход от исходной области к спектральной может привести к резкому снижению сложности решения поставленной задачи.

В общем, спектральное представление дискретной функции означает, что вместо вектора значений функции, используется вектор некоторых значений, полученных применением подходящего спектрального преобразования для рассматриваемой функции. Эти представления являются полностью эквивалентными. До тех пор, пока мы можем определить все значения функции, форма ее представления не имеет значения.

Однако, с практической точки зрения, есть очень важные различия.

Во-первых, может случиться, что прямое представление требует, например, сохранения большого количества минтермов в записи функции, а после применения правильного линейного преобразования, соответствующий вектор коэффициентов будет иметь гораздо более простую форму.

Во-вторых, из линейно преобразованного вектора значений функции, то есть спектра, часто можно определить некоторые свойства функции, которые было достаточно трудно определить непосредственно ( спектральный анализ). Например, анализ спектра позволяет выявить некоторые закономерности функции, позволяющие использовать конкретные виды схем для их аппаратной реализации. Отметим, что можно разместить на одном кристалле большое количество мощных вычислительных элементов, и это делает желательной высокую регулярность представления функции.

Настоящая работа посвящена обзору и анализу методов спектрального представления булевых функций. В том числе приведены основные характеристики БФ, позволяющие определит их применимость и полезность в различных приложениях, а также соотношения и методики их вычисления с использованием аппарата спектрального анализа.

1. 
   Основные теоретические положения
   

Для описания БФ и их свойств будем употреблять следующие обозначения и термины.

F₂ – конечное поле из двух элементов, 0 и 1. Операции в F₂ –умножение и сложение по модулю 2.

V_n – n-мерное векторное пространство над полем F₂, V_n = (F2)ⁿ. Сложение в пространстве V_nпобитовое по модулю 2. Через О обозначен нулевой вектор пространства V_n.

Единичные векторы e⁽ⁱ⁾ с единицей в i-й позиции и нулями в остальных образуют базис пространства V_n.

Булева функция от п переменных есть отображение из V_nв F₂. Также будем иметь дело также с расширенными булевыми функциями– отображе­ниями из V_nв Z (множество целых чисел).

Рассматривают и ещё более общие ^{псевдо-булевы функции: отображения из V}_n^{в R(множество действительных} чисел).

Множество всех булевых функций от п переменных обозначим F_п.

Число векторов пространства V_nравно 2ⁿ как число всевозможных комбинаций п базисных векторов с коэффициентами 0 и 1. По той же причине число элементов любого линейного подпространства при dim Е = т равно 2^m.

Булева или расширенная булева функция f{x) задана, если имеется список её значений при всех .

Алгебраическая нормальная форма булевых функций.

Каждая функция из F_п имеет единственное представление в виде алгебраической нормальной формыили АНФ (также употребляется термин «полином Жегалкина»). АНФ есть выражение булевой функции в виде

(1.1)

где Р{1, 2, ..., n}– множество всех подмножеств {1, 2, ..., n}(булеан), .

Алгебраическая степеньбулевой функции есть степень АНФ этой функ­ции (как многочлена от нескольких переменных).

Булева функция степени 1 называется аффинной. Её АНФ имеет вид

(1.2)

_{где ,} .

Термин «нелинейность» применяется для показателя нелинейности, использующего понятия веса Хэмминга и расстояния Хэмминга.

Весом Хэмминга или просто весом двоичного вектора называется число единиц среди его компонент. Вес Хэмминга булевой функцииесть вес вектора её значений. Обозначать вес вектора или функции будем wt(x) и wt(f).

Расстояние Хэммингамежду двумя функциями f и gесть вес функции . Другими словами, это число тех , на которых .

НелинейностьюN(f) булевой функции f называется расстояние Хэммин­га между f и множеством аффинных функций А_п.

Для количественной оценки нелинейности и других криптографических показателей вычисляют ряд характеристик булевых функций. В первую очередь это спектры Уолша-Адамара.

Также необходимо отметить, что для основных специальных классов БФ разработаны соответствующие методы синтеза схем, и эти методы, как правило, оказываются гораздо более эффективными, чем универсальные. Поэтому вопросы распознавания не­которых важных классов БФ по их спектрам Уолша и по автокорреляционным характеристикам привлекают интерес разработчиков дискретных схем (в последнее время – с использованием технологий VLSI), в том числе и для разработки средств тестирования эти схем.

1. 
   Спектральное представление булевых функций
   

Так как существует взаимно-однозначное соответствие между БФ и ее спектром, то задачи их анализа и синтеза удобно формулировать и решать в спектральной области, с использованием автокорреляционных харак­теристик, которые связаны с используемым базисом, двой­ными спектральными преобразованиями.

Решение этих задач существенно зависит от выбора базиса. В частности, от выбора базиса зависит число не­нулевых значений спектра. Целесообразно выбрать базис таким об­разом, чтобы каждая из базисных функций принимала сравнительно небольшое число значений, что упрощает реализацию БФ. В нашем случае целесообразно, чтобы базисные функции принимали значения 0, ±1.

Рассмотрим подробнее две системы функций (Уолша и Хаара), наиболее удобные для спектральных представлений систем БФ, встречающихся в настоящее время наиболее часто.

Функции Уолша являются кусочно-постоянными функциями
с интервалом задания аргумента , и определяются для любых натуральных i и m при следующим выражением:

(1.3).

Значения определяются из двоичных разложений

; (1.4)

Известно, что мно­жество 2^тфункций Уолша образует полную ортогональ­ную систему функций в пространстве кусочно-постоян­ных функций, определенных на 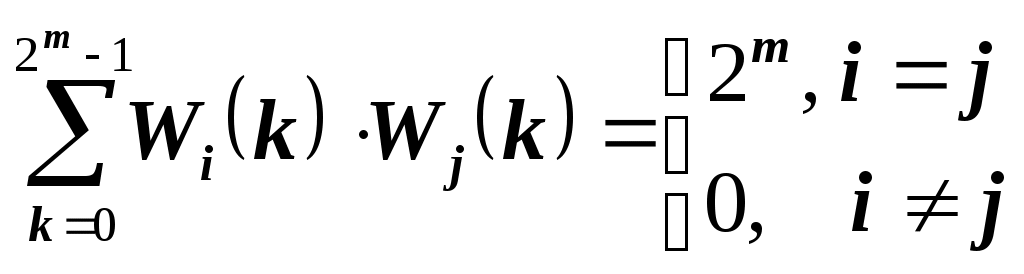, так что

. (1.5)

И, если - функция, такая, что

, (1. 6)

то .

Это свойство дает возможность использовать функции Уолша в качестве базиса при разложении в ортогональ­ные ряды кусочно-постоянных функций, представляю­щих системы БФ.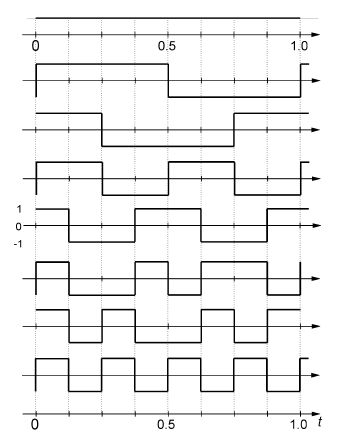


Рисунок 1. Функции Уолша в упорядочении по Уолшу
В дискретном случае система функций Уолша может быть представлена в виде матрицы Адамара.

 Матрица Адамара может быть сформирована рекурсивным методом с помощью построения блочных матриц по следующей общей формуле: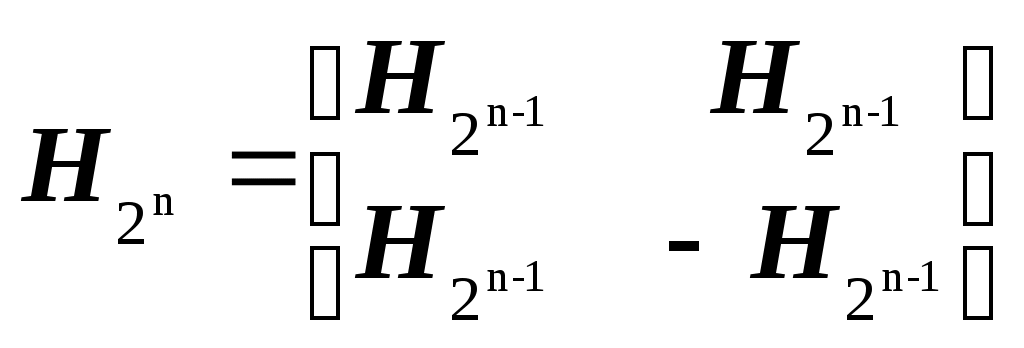

(1. 7)

Так может быть сформирована матрица Адамара размера .

Процедура формирования может быть выражена через оператор кронекеровского произведения на «порождающую» матрицу (базовую матрицу Уолша [3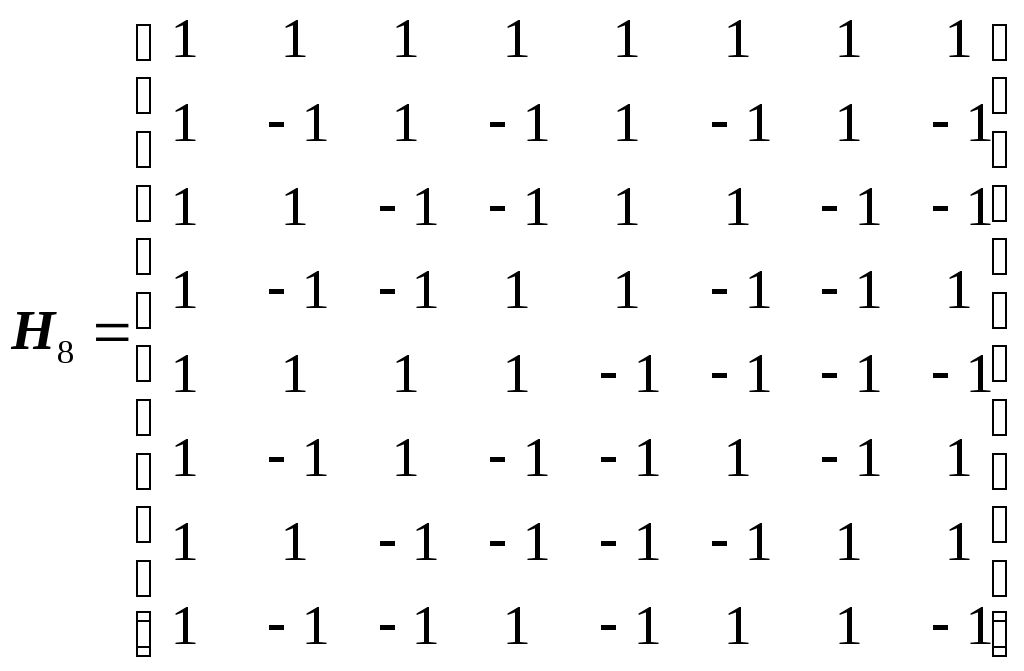]) следующим образом: .

Для матрица Адамара, соответственно описывающая систему функций Уолша порядка , выглядит следующим образом.

. (1. 8)

Каждая строка матрицы Адамара и является функцией Уолша.

В данном случае функции упорядочены по Адамару. Номер функции по Уолшу вычисляется из номера функции по Адамару путём перестановки бит в двоичной записи номера в обратном порядке с преобразованием результата из кода Грея. В некоторых случаях используется также упорядочение функций Уолша по Пэли [5, 22].

Кронекеровская структура матрицы позволяет легко ее факторизовать, в результате вычисление спектра Уолша выполняется по быстрому алгоритму.

Например, для преобразования Уолша порядка 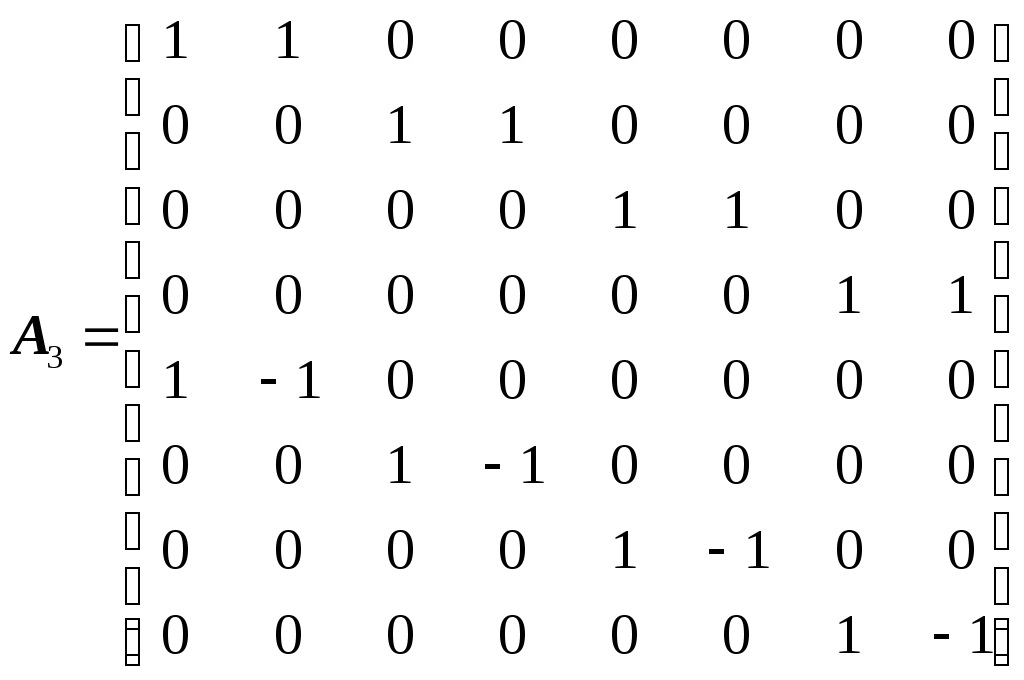верно следующее:

(1. 9)

(1.10)

Соответствующий сигнальный граф быстрого алгоритма преобразования Уолша (БПУ) с естественным порядком следования отсчетов сигнала и спектра приведен на следующем рисунке.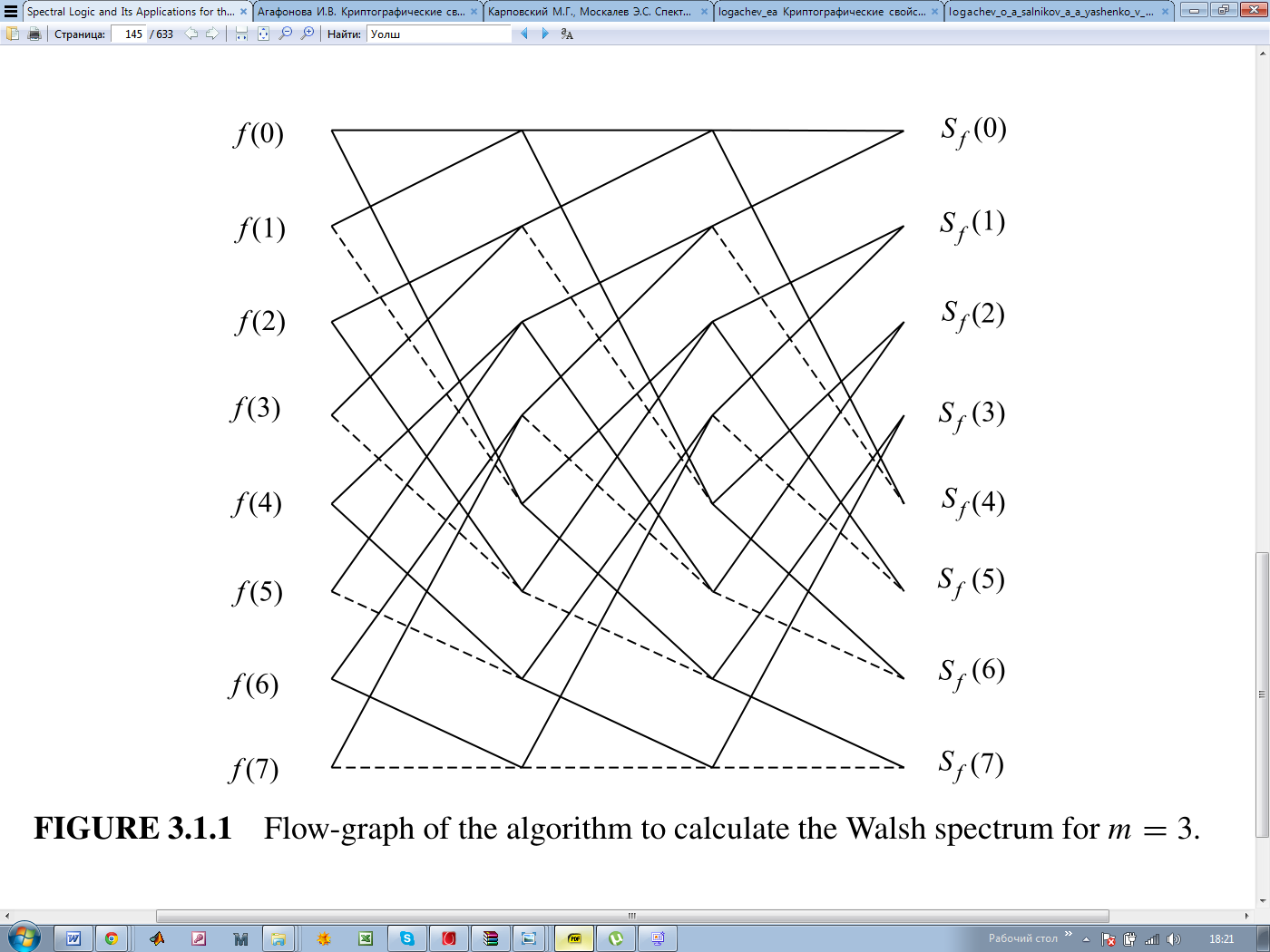



Рисунок 2. Сигнальный граф БПУ для N=8
Формула (3.1.3) дает нам матричный метод расчета спектра Уолша, заключающийся в m итерациях умножения исходного вектора на матрицу A_m, каждое из которых требует 2^m операций сложения или вычитания , так что общее число операций составляет m2^m, или m сложений или вычитаний для вычисления одного коэффициент Уолша.

2. 
   Характеристики булевых функций
   

Наиболее часто рассматриваемыми и наиболее полезными с точки зрения при разработке и анализе логических (булевых) функций являются следующие их характеристики.

1. 
   сбалансированность,
   
2. 
   порядок нелинейности
   
3. 
   корреляционный иммунитет
   
4. 
   ”бентность” – принадлежность к классу бент-функций
   
5. 
   расстояние до аффинных структур
   
6. 
   строгий лавинный критерий
   
7. 
   критерий распространения
   
8. 
   глобальный лавинный критерий
   

Приведем определения этих характеристик.

Булева функция f называется сбалансированной, если её таблица истинности содержит одинаковое число 0 и 1, т.е.

card{х: f(X) = 1} = card {х: f(X) = 0}.

Порядок нелинейности f определяется максимальным числом переменных, которые появляются в АНФ (f).

Функция f называется корреляционно-иммунной порядка m, если значение f является статистически независимым от любых m переменных (x_i1, x_i2, ..., x_im).

Булева функция f удовлетворяет критерию распространения степени k,если любой выходной бит изменяется с вероятностью строго ½при комплементарной замене к входных бит, то есть, если

Pr{f(x)f(xa)=1}= ½ для 1 //a// k.

Булева функция f удовлетворяет строгому лавинному критерию
(СЛК, SAC), если

Pr{f(x)f(xa)=1}= ½ для//a//=1,

т.е. имеет место равная вероятность изменения каждого выходного бита при изменении одного входного бита.

Глобальный лавинный критерий (ГЛК, GAC) булевой функции fхарактеризуется двоичной автокорреляционной функцией (dyadic autocorrelation function – DAC), которая определяется выражением

DAC(f)(а): = ∑x f(х) f (xa).

"Хороший" GAC означает, что DAC(f) близка к нулю для почти всех ненулевых значений а, и при а = 0 мы должны иметь DAC(f)(0) = 2n.

Двоичная автокорреляционная функция также является широко применяемым средством при анализе и синтезе дискретных устройств, а также при выборе ансамблей последовательностей с приемлемыми корреляционными свойствами для систем передачи данных с кодовым разделением каналов [].

Чем выше нелинейность булевой функции, тем сильнее функция отличаетсяот любой линейной функции. Вы­сокая нелинейность функции является одним из основных её крипто­графических свойств. Булевы функции от чётного числа перемен­ных, обладающие максимальной нелинейностью, а именно равной называются бент-функциями.

2. 
   Применение спектрального анализа булевых функций
   

С момента первого публичного упоминания [1] о спектральном представлении БФ, разработки в области применения спектрального анализа булевых функций велись в нескольких направлениях [₂-₃₁].

Можно выделить два основных, в которых исследования ведутся особенно активно. Это 1) анализ и синтез дискретных устройств и _{2) криптография.}

1. 
   Анализ и синтез дискретных устройств
   

В процессе проектирования дискретных устройств (ДУ) возникают две основные задачи: задача синтеза ДУ и задача анализа. Задача синтеза состоит в следующем: по заданной системе функций или по таблице истинности построить оптимальное, в некотором смысле, ДУ, их реализующее. Задача анализа состоит в описании функционирующего ДУ системой БФ, и в выявлении ее свойств. Решение задач анализа и синтеза может быть получено с помощью использования аппарата булевой алгебры.

Существует и другой подход к решению этих задач, основанный на использовании спектральных разложений систем функций алгебры ло­гики (ФАЛ). Для этого система ФАЛ представляется в виде функции непрерывного аргумента, а последняя – в виде суммы функционального ряда.

При этом верно положение о конечности представляющего ряда.

Пусть – кусочно-постоянная функция, представляющая некоторую систему БФ от m аргументов. Тогда

, (2.1)

. (2.2)

Разложение (2.1) является представлением в виде конечного ряда Фурье, и коэффициенты являются коэффициентами Фурье.

Из положения следует, что разложение в ряд по функциям Уолша любой кусочно-постоянной функции, представляющей некоторую систему БФ от т аргументов, содержит не более ₂^т членов; вес индексов функций Уолша в разложении не превышает т. Таким образом, если исходная система БФ определялась набором ₂^т значений, то и спектр по Уолшу этой системы содержит ₂^т<sub>в общем случае ненулевых членов.

Автокорреляционная функция БФ находится как</sub>

, (2.3)

где .

Проблема анализа БФ состоит в распознавании по заданной функции факта принадлежности ее к одному из известных классов (линейные, самодвойственные, по­роговые и т. д.). Важность этой проблемы связана с тем, что для основных специальных классов БФ разработаны соответствующие методы синтеза схем, и эти методы, как правило, оказываются гораздо более эффективными, чем универсальные. Поэтому этапу синтеза комбинацион­ной схемы часто предшествует этап анализа соответствую­щей системы БФ.

Ниже рассматриваются вопросы распознавания не­которых важных классов БФ по их спектрам по Уолшу и по автокорреляционным характеристикам. (Таблицы спектров и автокорреляционных характеристик отдель­ных классов БФ приведены в приложении [2]).

Кроме распознавания принадлежности БФ к одному из классов, в важна также очень близкая задача анализа корректирующих свойств БФ, т. е. задача определения того множества ошибок аргумен­тов, при котором БФ не меняет своего значения.

Рассмотрим некоторые теоретические положения, позволяющие классифицировать БФ по их спектрам [2, 3].

Линейные функции.

Пусть 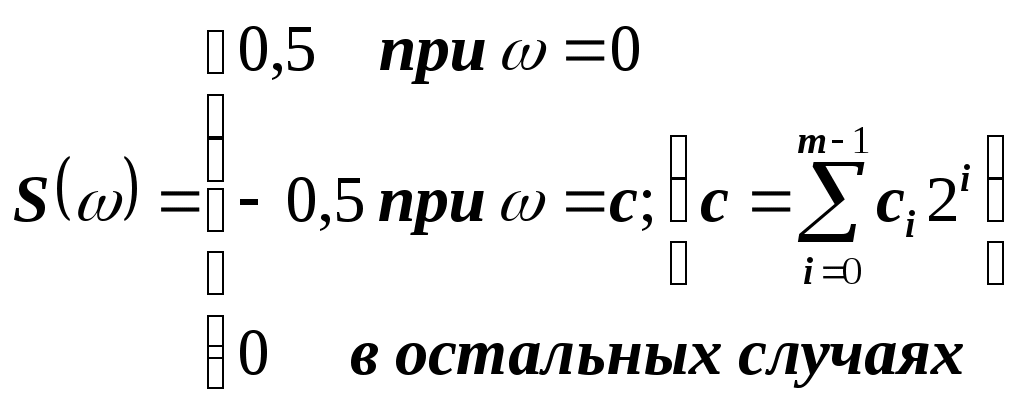(линейная функция). Тогда

(2.4)

. (2.5)

Таким образом, для распознавания линейности до­статочно вычислить спектр, и если спектр содержит всего одну ненулевую точку (не считая точку ), то БФ линейна и представима в виде .

Самодвойственные и антисамодвойственные функции.

Для того чтобы БФ f(z) была самодвойственной (антисамо-двойственной), необходимо и достаточно выполнение равен­ства: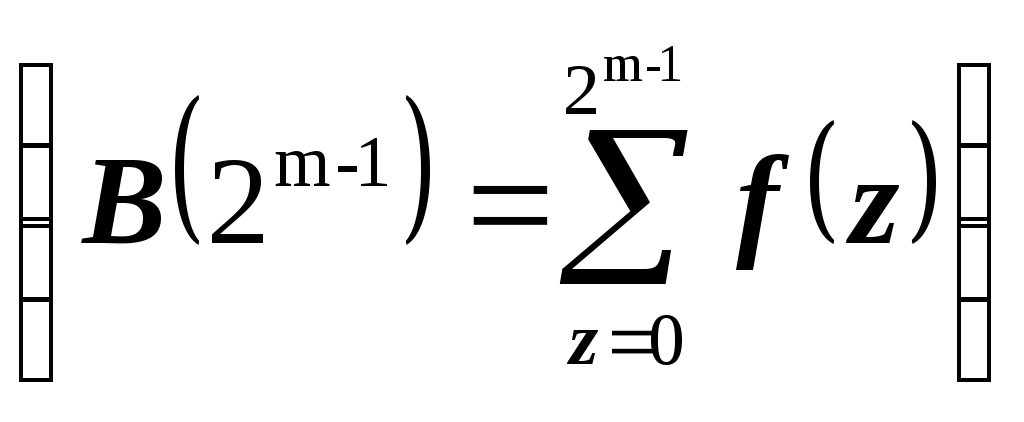

.



Таким образом, распознавание самодвойственности (антисамодвойственности) сводится к вычислению значения функции автокорреляции в точке 2^т– 1.

Квадратичные формы.

Булеву функцию будем называть квадратичной формой тогда и только тогда, если существуют такие, что

. (2.6)
Анализ корректирующей способности.

Пусть задана БФ , и γ есть некоторый двоичный вектор длины т. Будем говорить, что f(z) исправляет ошибку γ при входном наборе z0, если и только если f(z0γ)= f(z0) (mod 2).

Это означает, что если на входе любой схемы, реализующей f(z), имеется набор z0, и этот набор вследствие ошибок (в предыдущих схемах) исказился в тех компонентах, в которых вектор γ=1, то на выходе схемы сигнал не меняется, т. е. схема эту ошибку авто­матически исправляет. Таким образом, любая схема, реализующая f(z), без введения какой-либо избыточности исправляет целый класс ошибок.

Ошибку γ будем называть ошибкой кратности i= || γ ||, если число единиц в векторе γ (вес γ) равно i. Число ошибок кратности iпри всевозможных входных наборах длины т равно . Для f(z) обозначим число исправляемых i -кратных ошибок.

Вектор назовем корректирую­щим спектром функции f(z). Задача анализа корректи­рующей способности функции f(z) сводится к нахожде­нию ее корректирующего спектра.

Пусть задана БФ f(z) и ее автокорре­ляционная функция . Тогда

, (2.7)

где – число единиц в двоичном разложении .
Одним их подходов компактному тестированию и синтезу цифровых схем [2], а также к исследованию булевых функций в области криптографии [4] является их представление в виде наборов спектральных коэффициентов преобразования Уолша (в общем виде Адамара-Радемахера-Уолша, так как используются различные матрицы для преобразования).

Особенностью спектрального представления булевых функций является не только компактность самого теста, но и возможность непосредственного встраивания тестов в цифровое устройство для решения задач онлайновой диагностики и самодиагностики. Идея составления теста по спектральному преобразованию булевой функции восходит к работе [18], в которой предложен тестовый «синдром» (в дальнейшем без кавычек), назначением которого является различение логической функции, описывающей исправное устройство, от логической функции, измененной под воздействием возникшей в устройстве неисправности. В работе [18] тестовый синдром определен для трех логических операций (И, ИЛИ,  – исключающее ИЛИ) как отношение числа минитермов булевой функции, содержащей только одну операцию, к  , то есть  , где   означает число входов функции. Таким образом, синдром является некоторым числом , характеризующим функцию в зависимости от базиса её представления и рассчитывается для логических функций, содержащих только одну логическую операцию со значениями  .:

1) для многовходового логического И синдром (1)

2) для многовходового логического ИЛИ синдром ; (2)

3) для многовходового логического  – синдром  .(3)

Синдром  , получающийся в результате объединения двух синдромов  ,  разными операциями зависит от её вида:

1)  рассчитывается  ; (4)

2) И рассчитывается  ; (5)

3)  ИЛИ рассчитывается ; (6)

4)  рассчитывается  . (7)

Для всей комбинационной схемы, реализуемой функцией , для тестирования входа на изменение его значения на константу 0 или 1, существует её представление:

,

где   – выражения, не зависящие от ,

а «синдром»  . (8)

Процедура расчета комбинационной схемы с помощью представленного синдрома следующая. Начиная с представления схемы в виде булевой функции в дизъюнктивной нормальной форме рекурсивно применять формулы (1)-(8), исключая каждый раз по одной входной переменной. Такой расчет возможен в онлайновом режиме и не требует формирования и сохранения множества тестовых векторов, хотя требует дополнительных ячеек памяти и выходов комбинационной схемы. Также, такой синдром оказывается не применимым к некоторым видам схем. Для преодоления этих недостатков были предложены методы тестирования схем, использующие свойства спектральных преобразований булевых функций.

2. 
   Криптография
   

Исследование криптографических свойств булевых базируется на сформулированных в 1949 году Клодом Шенноном принципов преобразования инфор­мации для криптографических систем. Важнейшими из них являются [4, ₂₂]:

• принцип «перемешивания» — К.Шеннон дает неформальную трактовку хорошо известного в эргодической теории понятия для систем с конечным числом состояний;

• принцип «рассеивания» (diffusion), посредством которого «...статистическая структура сооб­щений, которая приводит к избыточности в сообщениях, "распыляется" в статистику больших длин, то есть в статистическую структуру, включающую длинные комбинации букв крипто­грамм» ;

• принцип «запутывания» (confusion), который «состоит в том, что соотношения между простыми статистиками в пространстве криптограмм и простыми подмножествами в пространстве ключей делаются весьма сложными и беспорядочными».

Принципы были сформулированы как эмпирические, не носящие формально-математического характера. Однако, эти принципы вместе с постоянно развивающимися методами криптографического анализа позволили во второй половине XX века сформулировать и изучить ряд математически строго формализованных криптографических свойств дискретных функций (см. п.1.2 настоящей работы).

Если говорить о соответствии упомянутых характеристик БФ и их спектров (подразумевается спектр Уолша-Фурье), то для некоторых из них верны приведенные ниже утверждения.

Если БФ f является сбалансированной, то ее спектр .
Преобразование Фурье-Уолша от диадной автокорреляционной функции (DAC (f)) является, в соответствии с теоремой Винера-Хинчина спектром мощности по Уолшу P(f) булевой функции f. Для функций F с хорошим GAC соответствующая P(f) является почти постоянной (имеет характеристику «белый шум»).
Для бент-функции верно следующее утверждение:

Булева функция f является бент-функцией, если модуль ее спектра Уолша постоянен и равен для всех .

Удовлетворение критериям (1) - (8), может привести к конфликтам. Например, таким:

(а) как правило, требуется, чтобы f была сбалансирована, поэтому не может быть бент-функцией

(б) бент-функции не существуют при нечетном n

(с) высокий порядок линейности означает низкую степень корреляционного иммунитета.

Утверждение. БФ f является сбалансированной, если .

Булева функция f удовлетворяет по определению критерию распространения по отношению к , если БФ ffa является сбалансированной. Здесь fa обозначает двоичное а-смещение БФ f, которое определяется как fa(x):=f(xa).

Булева функция f удовлетворяет по определению критерию распространения степени k, если она удовлетворяет критерию распространения для всех , таких, что 0  wt(а) k. В случае, если =1, говорим, что удовлетворяет строгому лавинному критерию.

Утверждение. БФ f удовлетворяет СЛК, если

для всех .
Следующее утверждение позволяет выразить расстояние от БФ f до линейной (аффинной) функции через ее спектр.

.

Утверждение (теорема Massey-Xiao). БФ f является корреляционно иммунной порядка m, если и только если для всех у с wt(а) m.

В терминологии анализа Уолша-Фурье это означает, что соответствующая функция является произведением более чем m функций Радемахера [5].

3. 
   Примеры применения спектрального анализа
   

Используем приведенные методы исследования спектра булевых функций на примере функции импликации, обозначаемой так: . Результатом импликации будет 0, если первый аргумент функции равен 1, а второй 0, т.е . Во всех остальных случаях значение функции будет равно 0.

Таблица истинности функции выглядит так.

№
1	0	0	1
2	0	1	1
3	1	0	0
4	1	1	1