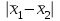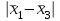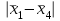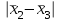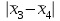контрольная. ПР3. Однофакторный дисперсионный анализ
 Скачать 273.33 Kb. Скачать 273.33 Kb.
|
|
Однофакторный дисперсионный анализ Часто необходимо сравнивать средние значения трёх и более числа выборок. В случае, когда необходимо сравнить средние значения большого числа выборок, используется метод дисперсионного анализа (ANOVA – Analysis of Variance), который устанавливает влияние отдельных факторов на изменчивость какого – либо признака, значения которого могут быть получены опытным путем в виде случайной величины Y. В зависимости от числа факторов, различают однофакторный и многофакторный дисперсионный анализ. Однофакторный дисперсионный анализ Величину Y называют результативным признаком, а конкретную реализацию фактора A – уровнем (группой) фактора A или способом обработки и обозначают через A(i) . Всего имеется c уровней фактора A. Обозначим их А(1),А(2),…,А(с) . Задачу однофакторного дисперсионного анализа можно продемонстрировать на следующем примере. Пример Необходимо определить существует ли разница между прочностью парашютов, сотканных из синтетических волокон разных поставщиков. Результаты эксперимента (сила разрыва) приведены в таблице . Таблица 2
. Пусть m1, m2,…, mс –математические ожидания результативного признака Υ при соответствующих уровнях фактора А. В данном примере результативный признак Υ- сила разрыва, уровни фактора А – группы поставщиков. Если при изменении уровня фактора групповые математические ожидания не изменяются, т.е. выполняется условие равенства мат.ожиданий : H0: m1=m2=…=mсто считается, что результативный признак не зависит от фактора А. В противном случае такая зависимость имеется (H1: не все мат.ожидания равны). Поскольку мат.ожидания не известны, необходимо подтвердить гипотезу об их равенстве на основе выборочных данных. Эту гипотезу Н0: m1 = m2=…= mс можно подтвердить с помощью F – критерия Фишера, если выполняются следующие условия: наблюдения должны быть случайными, независимы и проводиться в одинаковых условиях. экспериментальные данные должны иметь нормальный закон распределения их дисперсии должны быть одинаковыми. Если эти условия выполняются, то можно приступать непосредственно к процедуре дисперсионного анализа, т.е. к проверке гипотезы о равенстве средних величин: Н0: m1 = m2=…= mс Проверить эту гипотезу можно, изучая вариации отдельных значений признака. Общая изменчивость значений признака может быть вызвана как изменчивостью значений признака между различными группами (межгрупповая вариация), так и изменчивостью значений признака внутри группы (внутригрупповая вариация). Для измерения степени вариации используется показатель – сумма квадратов отклонений. Общая (полная) вариация определяется полной суммой квадратов отклонений. 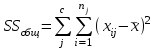 где 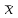 - общее среднее. - общее среднее.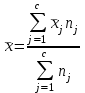 . .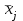 - среднее значение в j –ой группе - среднее значение в j –ой группе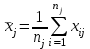 Межгрупповая вариация, вызванная влиянием фактора A на X определяется по формуле 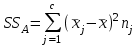 , ,Внутригрупповая вариация определяется равенством 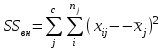 В общем случае выполняется равенство 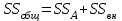 , т.е. полная вариация значений признаков определяется суммой межгрупповой и внутригрупповой вариации. , т.е. полная вариация значений признаков определяется суммой межгрупповой и внутригрупповой вариации.Для проверки гипотезы о равенстве средних величин используется F-критерий Фишера, статистика которого определяется отношением. 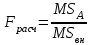 Статистика F-критерия подчиняется распределению Фишера с числом степеней свободы 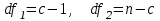 , где n – общее число наблюдений, c - число уровней фактора A. , где n – общее число наблюдений, c - число уровней фактора A.Показатель MS определяется как сумма квадратов отклонения, приходящаяся на одну степень свободы. 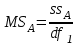 , ,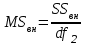 , ,где SSA – сумма квадратов отклонения, вызванная влиянием фактора A на X, а SSвн - сумма квадратов отклонения, вызванная влиянием остаточных факторов на Y. Пример. Необходимо определить, имеют ли парашюты, сотканные из синтетических волокон от 4 разных поставщиков, одинаковую прочность. Проведена экспериментальная проверка парашютов на прочность. Результаты в таблице 1. Табл. 1
Для проверки гипотезы о равенстве средних значений определяется правосторонняя критическая область, т.е. вычисляется Fкрпри уровне значимости 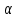 (см. функцию Excel F.ОБР.ПХ) и проверяется попадание рассчитанного значения Fрасч – статистики в интервал (Fкр;+∞). Если попадает, то гипотеза отклоняется, в противном случае принимается. (см. функцию Excel F.ОБР.ПХ) и проверяется попадание рассчитанного значения Fрасч – статистики в интервал (Fкр;+∞). Если попадает, то гипотеза отклоняется, в противном случае принимается. Прежде чем использовать F – критерий Фишера необходимо установить на основе имеющихся выборочных данных, являются ли генеральные дисперсии результативного признака при различных условиях фактора одинаковыми или нет. Проверяется гипотеза H0:σ1=σ2=σ3…=σ против гипотезы Н1: не все дисперсии одинаковы. Для этого воспользуемся критерием Левенэ. Вычисляются абсолютные величины разностей между наблюдениями и медианами в каждой группе (см. пример). Результат представлен в таблице 2. Табл. 2.
Далее выполняем однофакторный дисперсионный анализ полученных значений абсолютных разностей. Для проведения однофакторного дисперсионного анализа используем инструмент в пакете анализа Excel, который так и называется « Однофакторный дисперсионный анализ». Здесь задаются следующие параметры: входной интервал (вводится вся таблица с исходными данными); вид группирования (по столбцам); выходной интервал. Результаты анализа для примера, приведенного выше (табл.2), сведены в таблицу 3. Табл. 3
Поскольку Fрасч = 0,2068 < 3,2388, нулевая гипотеза о равенстве дисперсий не отклоняется. Между дисперсиями внутри каждой группы существенной разницы нет, т. е. условие об однородности данных выполняется . Далее проводим однофакторный дисперсионный анализ для исходных данных (табл. 1). Результаты анализа для примера (табл.1), выведены в таблицу 4. Табл. 4
Поскольку Fрасч = 3,4616 При обнаружении значительных различий между математическими ожиданиями необходимо определить, какие именно группы отличаются друг от друга. Для этого используется процедура множественного сравнения Тьюки – Крамера, описанная ниже. Вычисляются разности 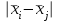 , где i ≠ j – номера групп, между средними значениями c(c – 1) групп; , где i ≠ j – номера групп, между средними значениями c(c – 1) групп;Вычисляется критический размах процедуры Тьюки – Крамера по формуле 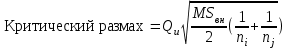 где Qu –верхнее критическое значение распределения стьюдентизированного размаха, имеющего c степеней свободы в числителе df1 = c и df2 = n степеней свободы в знаменателе, n-общее число наблюдений, n1 и n2 число наблюдений в i-ой и j-ой группах соответственно. Каждая из c(c – 1)/2 пар разностей математических ожиданий сравнивается с рассчитанным критическим размахом. Элементы пары считаются различными, если модуль разности между ними 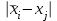 превышает критический размах. превышает критический размах. Чтобы провести анализ, необходимо вычислить критический размах и сравнить с абсолютными отклонениями. Для этого по таблице 4 определим величины MSвн = 6,094 и ni = nj = 5. Далее находим величину Qu - верхнее критическое значение стьюдентизованного распределения с числом степеней свободы 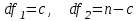 из таблицы 4, где n = 20 – общее число наблюдений, c = 4 - число уровней фактора A (число поставщиков). Таким образом, df1 = 4, df2 = 16. По таблице 6 определяем Qu = 4,05. из таблицы 4, где n = 20 – общее число наблюдений, c = 4 - число уровней фактора A (число поставщиков). Таким образом, df1 = 4, df2 = 16. По таблице 6 определяем Qu = 4,05.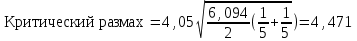 Результаты сравнения приведены ниже. Табл. 5
Поскольку 4,74 > 4,71, статистически значимая разница существует между первым и вторым поставщиком. Все остальные пары состоят из практически одинаковых величин. Таблица стьюдентизованного распределения Qu κ = df1, ν = df2. Табл. 6 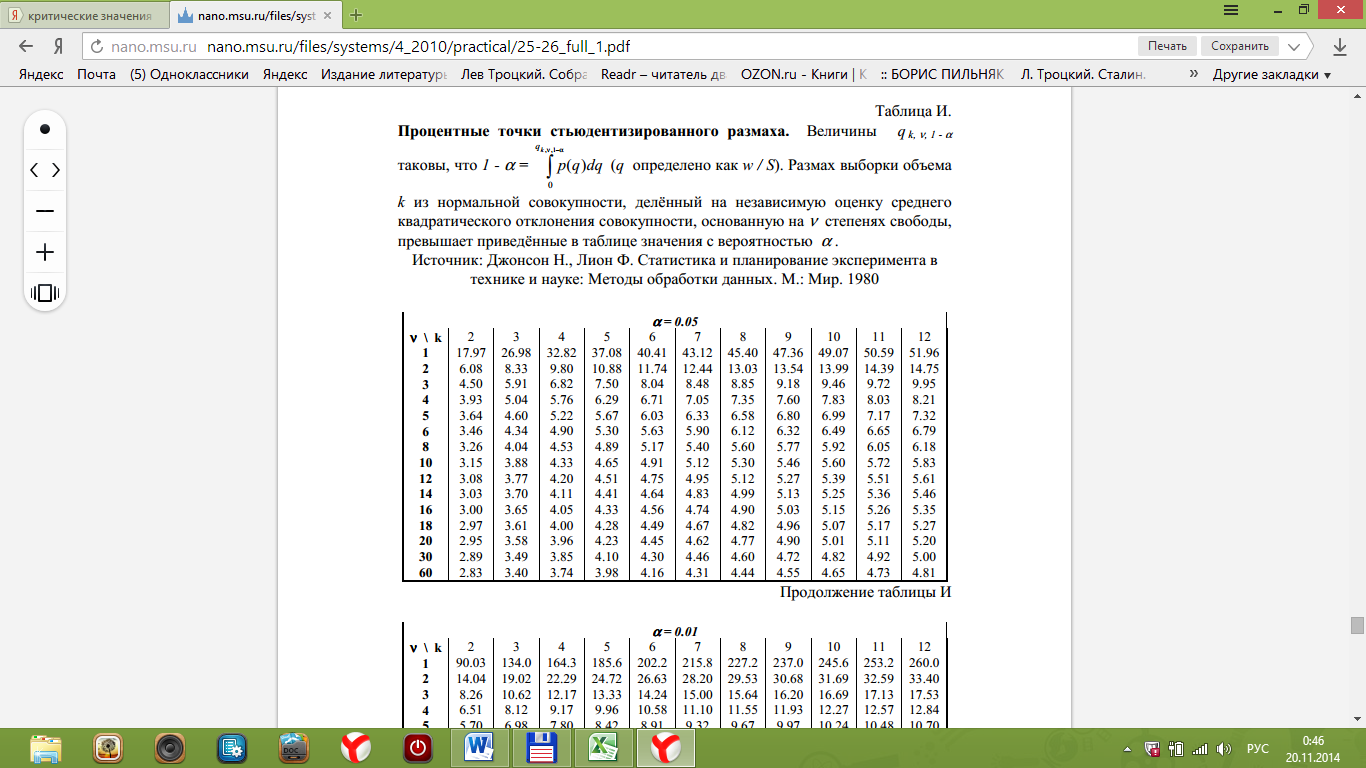 Если значение ν > 60 используйте последнюю строку ЗАДАНИЕ Работа выполняется в табличном процессоре MS Excel с использованием статистических функций и пакета анализа. Статистическая информация для выполнения заданий генерируется студентами самостоятельно с помощью инструмента анализа «Генерация» пакета ECXEL в соответствии с вариантом задания (№ по списку).
mx – математическое ожидание σx – стандартное отклонение. Статистическую информацию для выполнения задания генерируем с помощью инструмента анализа: Сервис→Анализ данных…→Генерация случайных чисел. Для генерации используем исходные данные своего варианта, характеризующие генерируемый ряд случайных чисел (выборку). Пример Математическое ожидание mx =5; Стандартное отклонение σx = 19. В соответствии с исходными данными сгенерирован ряд из 31 значение случайной величины (табл.1), распределённой нормально. На рис.1 представлено окно «Генерация случайных чисел», в которое введены mx, σx. 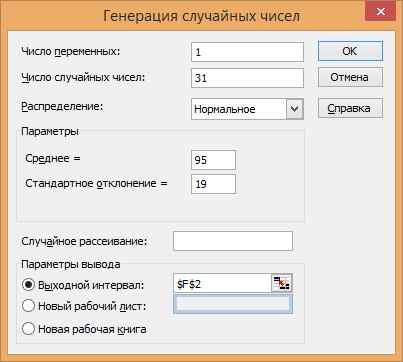 Рис.1. Диалоговое окно «Генерация случайных чисел» Сгенерировать 4 нормально распределенные переменные. Первые 3 переменные генерируется в соответствии с Вашим вариантом. При генерации четвертой переменной математическое ожидание увеличивается на 2, а стандартное отклонение не изменяется Используя модифицированный критерий Левенэ проверить гипотезу о равенстве дисперсий. Используя инструмент анализа « Однофакторный дисперсионный анализ» проверить гипотезу о равенстве математических ожиданий. При обнаружении значительных различий между математическими ожиданиями необходимо определить, какие именно группы отличаются друг от друга, используя процедуру множественного сравнения Тьюки – Крамера | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||