Практика. Определение корреляционных зависимостей между геофизическими параметрами и физическими характеристиками горных пород

• Название: Определение корреляционных зависимостей между геофизическими параметрами и физическими характеристиками горных пород
• Анкор: Практика
• Дата: 24.10.2020
• Размер: 129.7 Kb.
• Имя файла: Prakticheskaya_rabota_1.docx
• Тип: Документы; #145408

ЮРГПУ (НПИ) Кафедра ПГ	Определение корреляционных зависимостей между геофизическими параметрами и физическими характеристиками горных пород	1
Цель работы: изучить физико-механические свойства пород и определить корреляционные зависимости между геофизическими параметрами и физическими характеристиками горных пород. Пояснение к работе. При инженерно-геологических и гидрогеологических изысканиях возникает необходимость определять пористость, трещиноватость, прочностные параметры, водонасыщенность и другие физико-механические и водноколлекторские свойства горных пород. Теоретические и экспериментальные исследования позволили установить связь между этими параметрами и физическими свойствами пород, определяемыми при геофизических исследованиях как в лабораторных условиях на образцах, так и в естественном залегании пород. 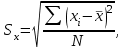С помощью корреляционного анализа оценивается степень близости корреляционной зависимости к функциональной, которая характеризуется коэффициентом корреляции: где - среднее значение х; - среднее значение у; N - число измерений; Sx, Sy- средние квадратические отклонения: Коэффициент корреляции rизменяется от -1 до +1. При r = 0 линейная связь между х и уотсутствует, а при r= ±1 связь между х и уфункциональная. Путем корреляционного анализа определяется характер связей и уравнение регрессии: Эмпирическое распределение двух величин может быть представлено в виде поля корреляции, на котором могут быть даны линии регрессии. На рис. 1, а показано поле корреляции и линия регрессии плотности и скорости распространения продольных волн (коэффициент корреляции положительный - с увеличением одной величины другая тоже возрастает); на рис.1 ,б представлено поле корреляции и линия регрессии плотности базальтов Армении и пористости (коэффициент корреляции отрицательный - с увеличением одной величины другая уменьшается). Рис. 1. Поле корреляции и линия регрессии скорости распространения упругих волн, плотности и пористости а - коэффициент корреляции положительный; б - коэффициент корреляции отрицательный Физические свойства горных пород могут быть связаны между собой не только линейной, но и более сложной зависимостью - в этом случае речь идет о нелинейной корреляции (например, ломаная регрессия, криволинейные уравнения корреляционной связи и т. д.). При геофизических исследованиях нередко бывает, что интересующий нас параметр зависит от двух и даже большего числа других параметров. Корреляция таких величин называется множественной. Статистическую обработку большого числа измерений физических параметров образцов и установление сложных корреляционных зависимостей целесообразно проводить с помощью ЭВМ. Существует большая библиотека стандартных программ, позволяющих вычислить статистические характеристики и проанализировать корреляционные зависимости с оценкой достоверности получаемых результатов. Порядок выполнения работы По исходным данным заданного варианта составить уравнение регрессии и вычислить коэффициент корреляции. По полученному уравнению регрессии построить график зависимости между заданными параметрами. Последовательность выполнения задания: Для того чтобы составить уравнение регрессии и вычислить коэффициент корреляции, надо определить для имеющихся значений хиуследующие величины: 1) среднее значение ; 2) среднее значение ; 3) для каждого значения xiего отклонение от среднего значения , т. е.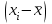 , и квадрат этого отклонения ; 4) для каждого значения yiего отклонение от среднего значения , т. е. , и квадрат этого отклонения ; 5) для каждого значения xiи yi произведение их отклонения от среднего, т. е. ; 6) сумму ; 7) сумму ; 8) сумму ; 9) среднеквадратичное отклонение Sx; 10) среднеквадратичное отклонение Sy; 11) коэффициент корреляции r ; 12) составить уравнение регрессии. Сделать вывод: при r = …., имея уравнение регрессии и зная скорость распространения продольных волн, можно оценить коэффициент Пуассона. Ход работы. 10 вариант. Определить коэффициент корреляции и уравнение регрессии для эмпирической зависимости между модулем упругости (модулем Юнга) и удельным электрическим сопротивлением для диабазов района Братской ГЭС (табл. 1.1). 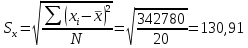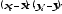Среднеквадратичное отклонение: Среднеквадратичное отклонение: = 53,7 Коэффициент корреляции: Таблица 1.1 № п/п x (p) y (Eд) 1 920 780 219 27,25 47961 742,56 5967,8 2 510 840 -191 87,25 36481 7612,6 -16665 3 700 820 -1 67,25 1 4522,6 -67,25 4 820 700 119 -52,75 14161 2782,6 -6277 5 650 690 -51 -62,75 2601 3937,6 3200,3 6 620 710 -81 -42,75 6561 1827,6 3462,8 7 880 800 179 47,25 32041 2232,6 8457,8 8 730 790 29 37,25 841 1387,6 1080,3 9 570 690 -131 -62,75 17161 3937,6 8220,3 10 610 700 -91 -52,75 8281 2782,6 4800,3 11 790 780 89 27,25 7921 742,56 2425,3 12 900 840 199 87,25 39601 7612,6 17363 13 890 820 189 67,25 35721 4522,6 12710 14 550 700 -151 -52,75 22801 2782,6 7965,3 15 540 690 -161 -62,75 25921 3937,6 10103 16 550 705 -151 -47,75 22801 2280,1 7210,3 17 750 770 49 17,25 2401 297,56 845,25 18 790 790 89 37,25 7921 1387,6 3315,3 19 620 710 -81 -42,75 6561 1827,6 3462,8 20 630 730 -71 -22,75 5041 517,56 1615,3 =701 =752,75 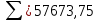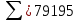Путем корреляционного анализа определяется характер связей и уравнение регрессии: 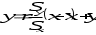Вычисляем значение y для каждого значения x и по этим значениям строим таблицу 1.2. Таблица 1.2 № п/п X (p) Y (Eд) 1 920 803,0576 2 510 708,8744 3 700 752,5203 4 820 780,0861 5 650 741,0345 6 620 734,1431 7 880 793,869 8 730 759,4117 9 570 722,6573 10 610 731,8459 11 790 773,1946 12 900 798,4633 13 890 796,1661 14 550 718,063 15 540 715,7659 16 550 718,063 17 750 764,006 18 790 773,1946 19 620 734,1431 20 630 736,4402 По данным таблицы 1.2 строим график зависимостей между модулем упругости (модулем Юнга) и удельным электрическим сопротивлением для диабазов района Братской ГЭС. График зависимостей между модулем упругости (модулем Юнга) и удельным электрическим сопротивлением для диабазов района Братской ГЭС. Вывод: изучил физико-механические свойства пород и определил корреляционные зависимости между геофизическими параметрами и физическими характеристиками горных пород, нашел коэффициент корреляции и уравнение регрессии; по полученному уравнению регрессии построил график зависимостей между модулем упругости (модулем Юнга) и удельным электрическим сопротивлением для диабазов района Братской ГЭС. И по этому графику увидел, что с увеличением модуля упругости, увеличивается удельное электрическое сопротивление.
Работу выполнил студент группы 3-2а Старовойтов В.Ю.	Работу принял старший преподаватель кафедры НТиТ Гроссу А.Н.	Дата