сопромат 2 лаба. Определение модуля упругости и коэффициента Пуассона для стали

• Название: Определение модуля упругости и коэффициента Пуассона для стали
• Анкор: сопромат 2 лаба
• Дата: 03.11.2021
• Размер: 131.93 Kb.
• Имя файла: laba_2_sopromat_s_raschetami_i_grafikami.docx
• Тип: Отчет; #262631

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего

образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра механики
Отчет по лабораторной работе № 2
По дисциплине : Сопротивление материалов
Тема: «Определение модуля упругости и коэффициента Пуассона для стали»

Выполнил: студент гр. МЦ-20 ___________ / Хатетовский Я.Е. /

( Подпись)

Проверил: ассистент ___________ /Семёнов В.И./

(Подпись)

Дата:

Санкт-Петербург

2021 год

Цель работы: изучение способа измерения модуля упругости и коэффициента Пуассона, определение упругих констант стали.

Теоретические сведения:

При растяжении стержня в нем возникают продольные напряженияσ_Z и продольныеε_Z и поперечныеε_X деформации. При растягивающих усилиях, соответствующих напряжениям, не превышающим предел текучести, продольные напряжения и деформации связаны соотношением, называемым законом Гука:

σ=E·ε,

где Е – модуль упругости, который также называют модулем Юнга.

Кроме продольных деформаций, в стержне возникают в плоскости, перпендикулярной его оси (поперечные деформации), величину

μ=−ε_X·ε_Z

называют коэффициентом Пуассона.

При нагружении стержня в пределах упругой области коэффициент Пуассона является постоянной величиной и связь между продольными и поперечными деформациями в стержне линейна.

Экспериментальная часть.

Таблица 1. Геометрические параметры образца

t,мм	b,мм	l,мм	F,мм2
6,6	40	40,5	264

Таблица 2. Протокол испытаний

Измеренные величины						Рассчитанные величины
P, кН	∆Z, мм	-∆X, мм	εZ ̲TP ˟10-6	-εX ̲TP˟10-6	σ, мПа		εZ˟10-6	-εX˟10-6
3,2	0,003	0,001	81	23	0,0121		74,07	25
6,04	0,006	0,003	179	52	0,0229		148,14	75
9,2	0,01	0,004	299	87	0,0349		246,91	100
12	0,013	0,005	405	118	0,0455		320,99	125
15	0,017	0,007	528	153	0,0568		419,75	175
18,8	0,022	0,009	682	197	0,0712		543,21	225
21	0,026	0,009	780	225	0,0796		641,98	225
24	0,031	0,011	905	261	0,0909		765,43	275
27	0,035	0,012	1029	297	0,1023		864,2	300

Расчётные формулы: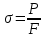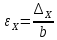







Примеры расчетов:







F=b*t=6,6*40=264

Графическая часть.



График 1.



График 2.



График 3.



График 4.

Вывод: в ходе лабораторной работы изучили способ измерения модуля упругости и коэффициента Пуассона, определили упругие константы стали.

Для зависимостей σ(ε_Z), рассчитанными по микрометрам и тензорезисторам, модуль упругости составил:

E=10² МПа

Для зависимости ε_X(ε_Z), рассчитанной по микрометрам, коэффициент Пуассона составил:

µ=-0,3754

Для зависимости ε_X(ε_Z), рассчитанной по тензорезисторам, коэффициент Пуассона составил:

µ=-0,2889