ргр сопр. ргр2 гоголева. Определение положения главных центральных осей инерции для сложных сечений
 Скачать 217.57 Kb. Скачать 217.57 Kb.
|
|
Определение положения главных центральных осей инерции для сложных сечений
Найти положение главных центральных осей инерции и величину главных моментов инерции для заданного сечения, приведенного на рис. 1 а. Сечение составлено из двутавра № 4 (рис. 1 б), прямоугольника (рис. 1 в) и швеллера № 20 (рис. 1 г). Из сортамента прокатной стали выписываем необходимые данные. При этом присваиваем двутавру индекс 1, листу - индекс 2, а швеллеру - индекс 3. а) 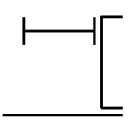 б) б)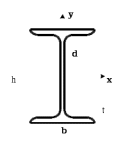 в)  г) г) 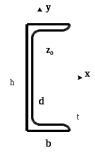 Рис. 1: а) – составное сечение; б) – двутавр; в) – лист; г) – швеллер. Двутавр № 12(ГОСТ 8239-89): h = 160 мм, b = 81 мм, d = 5 мм, t = 7,8 мм, A = 20,2 см2, Ix = 874см4 , Iy = 58,6 см4. Прямоугольный лист: h = 24 см, b = 1,8 см. Швеллер (ГОСТ 8240 - 89): h=200мм, b=76мм, d=5,2мм, t=9мм, А=23,4см2 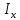 =7см4 =7см4 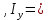 8 см4, 8 см4, 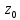 =9см =9см Вычертим сечение в масштабе, показав все необходимые оси и размеры (рис. 2). Для каждого сечения выберем прямоугольную систему координат с началом в центре тяжести сечения. Системы координат выбираются параллельными друг другу. Обозначим все оси соответствующими индексами. Вычислим площадь всего сечения как сумму площадей простых сечений: 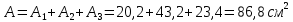 Определим осевые и центробежные моменты инерции каждого сечения относительно осей, проходящих через их центр тяжести. Для двутавра: 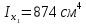 , , 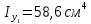 , , 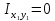 . .Для прямоугольника: 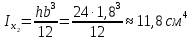 , , 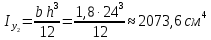 , , 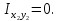 Для швеллера: 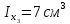 , , 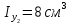 , , | ||||||||||||||||||||||||
