Основные факторы стереометрии Лобачевского. Курсовая работа Основные факты стереометрии Лобачевского. Основные факты стереометрии Лобачевского Содержание

• Название: Основные факты стереометрии Лобачевского Содержание
• Анкор: Основные факторы стереометрии Лобачевского
• Дата: 23.05.2022
• Размер: 158.84 Kb.
• Имя файла: Курсовая работа Основные факты стереометрии Лобачевского.docx
• Тип: Реферат; #545863

Основные факты стереометрии Лобачевского

Содержание
Введение………………………………………………….……………………….3

Глава 1. Стереометрия  Лобачевского……………………………….………….5

1.1 Факты стереометрии Лобачевского ………………………...……………….5

1.2 Модель Пуанкаре плоскости Лобачевского. Точки и прямые. ……...…….7

1.3 Модель Пуанкаре плоскости Лобачевского. Вторая группа аксиом………8

1.4 Модель Пуанкаре плоскости Лобачевского. Третья группа аксиом.……..9

1.5 Модель Пуанкаре плоскости Лобачевского. Четвертая группа аксиом….11

1.6 Модель Пуанкаре плоскости Лобачевского. Пятая группа аксиом………12

1.7 Треугольники и четырехугольники на плоскости Лобачевского……...…13

1.8 Окружность в модели Пуанкаре плоскости Лобачевского………….........14

1.9 Замечательные точки и замечательные прямые треугольника на плоскости Лобачевского в модели Пуанкаре………………………………………………18

Глава 2. Решение задач……………………………………………………….....20

Заключение…………………………………………………………………........24

Список литературы………………………………………………………..…….25

Введение
Стереометрия Лобачевского, как ее теперь называют, является крупнейшим завоеванием науки и составляет целую эпоху в развитии математики и смежных с ней наук. Деятельность Лобачевского вызывает изумление. Лобачевскому было всего 34 года, когда он решил «многовековую» проблему пятого постулата из «Начал» Евклида и построил свою, неевклидову геометрию. Имя Лобачевского известно всему миру. Он вошел в историю математики как революционер в науке и «Коперник геометрии».

Николай Иванович Лобачевский решил проблему, над которой человечество бесплодно билось более двух тысяч лет. Анализируя попытки доказать пятый постулат, Лобачевский сделал чрезвычайно смелый вывод о его недоказуемости. Раз пятый постулат недоказуем как теорема, то принципиально возможна другая геометрия, отличная от евклидовой, – неевклидова геометрия, отправной точкой которой является отрицание пятого постулата.

Стереометрия Лобачевского – один из видов неевклидовой геометрии, то есть геометрическая теория, основанная на тех же основных посылках, что и обычная геометрия, за исключением 11-й аксиомы (пятый постулат), которая заменяется на аксиому о параллельных Лобачевского: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие ее.

Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать, то есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет. Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика. Ведь при ближайшем рассмотрении оказывается, что в неевклидовой геометрии не только не говорится о пересечении параллельных прямых, но и не говорится о параллельных прямых вообще – разговор здесь идет именно о непересекающихся прямых, находящихся на одной плоскости.

Актуальность темы работы заключается в том, что стереометрия Лобачевского  связана с  евклидовой геометрией, и её изучение дает возможность шире и разносторонне ориентироваться  в основных фактах геометрии Евклида.  Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и до сегодняшнего дня способствует более глубокому пониманию окружающего нас материального мира. Теория стереометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир, это интересный, необычный и прогрессивный раздел современной геометрии.

Объектом исследования является геометрия Лобачевского.

Предметом является теоремы, аксиомы, свойства и доказательства в стереометрии Лобачевского.

Цель работы – изучение основных фактов стереометрии Лобачевского и применение их на практике при решении задач.

Задачи:

1) изучить литературу по теме исследования;

2) сформулировать теоремы;

3) привести доказательства к теоремам;

4) привести примеры задач по геометрии Лобачевского.

Курсовая работа включает введение, 2 главы, заключение и список литературы.


Глава 1. Стереометрия  Лобачевского

1.1 Факты стереотметрии Лобачевского

Ло­ба­чев­ский стро­ил свою гео­мет­рию, от­прав­ля­ясь от ос­нов­ных геометрических по­ня­тий и сво­ей ак­сио­мы, и до­ка­зы­вал тео­ре­мы геометрическим ме­то­дом, по­доб­но тому, как это де­ла­ет­ся в гео­мет­рии Евк­ли­да. Ос­но­вой слу­жи­ла тео­рия па­рал­лель­ных ли­ний, т. к. имен­но здесь на­чи­на­ет­ся от­ли­чие геометрии Лобачевского от гео­мет­рии Евк­ли­да.

Все тео­ре­мы, не за­ви­ся­щие от ак­сио­мы о па­рал­лель­ных, об­щи обе­им гео­мет­ри­ям и об­ра­зу­ют т. н. аб­со­лют­ную гео­мет­рию, к ко­то­рой от­но­сят­ся, например, тео­ре­мы о ра­вен­ст­ве тре­уголь­ни­ков. Вслед за тео­ри­ей па­рал­лель­ных строи­лись др. раз­де­лы, вклю­чая три­го­но­мет­рию и на­ча­ла ана­ли­ти­че­ской и диф­фе­рен­ци­аль­ной гео­мет­рий. Ни­же пе­ре­чис­ле­ны неск. фак­тов геометрии Лобачевского, ус­та­нов­лен­ных са­мим Н. И. Ло­ба­чев­ским, ко­то­рые от­ли­ча­ют её от гео­мет­рии Евк­ли­да.

1) В стереометрии Лобачевского не су­ще­ст­ву­ет по­доб­ных, но не рав­ных тре­уголь­ни­ков; тре­уголь­ни­ки рав­ны, ес­ли их уг­лы рав­ны. По­это­му су­ще­ст­ву­ет аб­со­лют­ная еди­ни­ца дли­ны, т. е. от­ре­зок, вы­де­лен­ный по сво­им свой­ст­вам, по­доб­но тому, как пря­мой угол вы­де­лен свои­ми свой­ст­ва­ми. Та­ким от­рез­ком мо­жет слу­жить, напр., сто­ро­на пра­виль­но­го тре­уголь­ни­ка с дан­ной сум­мой уг­лов.

2) Сум­ма уг­лов вся­ко­го тре­уголь­ни­ка мень­ше ππ и мо­жет быть сколь угод­но близ­кой к ну­лю. Это вид­но на мо­де­ли Пу­ан­ка­ре. Разность π−(α+β+γ)π−(α+β+γ), где α,β,γα,β,γ – уг­лы тре­уголь­ни­ка, про­пор­цио­наль­на его пло­ща­ди.

3) Че­рез точ­ку, не ле­жа­щую на дан­ной пря­мой, про­хо­дит бес­ко­неч­но мно­го пря­мых, не пе­ре­се­каю­щих прямую и на­хо­дя­щих­ся с ней в од­ной плос­ко­сти; сре­ди них есть две край­ние, ко­то­рые назы­ва­ют­ся па­рал­лель­ны­ми пря­мой в смыс­ле Ло­ба­чев­ско­го. В мо­де­лях Клей­на и Пу­ан­ка­ре они изо­бра­жа­ют­ся хор­да­ми (ду­га­ми ок­руж­но­стей), имею­щи­ми с хор­дой (ду­гой) об­щий ко­нец.

4) Ес­ли пря­мые име­ют об­щий пер­пен­ди­ку­ляр, то они бес­ко­неч­но рас­хо­дят­ся в обе сто­ро­ны от не­го. К лю­бой из них мож­но вос­ста­но­вить пер­пен­ди­ку­ля­ры, ко­то­рые не дос­ти­га­ют др. пря­мой.

5) Ли­ния рав­ных рас­стоя­ний от пря­мой есть не пря­мая, а осо­бая кри­вая, на­зы­вае­мая эк­ви­ди­стан­той или ги­пер­цик­лом.

6) Пре­дел бес­ко­неч­но рас­ту­щих ок­руж­но­стей есть не пря­мая, а осо­бая кри­вая, на­зы­вае­мая пре­дель­ной ок­руж­но­стью или ори­цик­лом.

7) Пре­дел сфер бес­ко­неч­но уве­ли­чи­ваю­ще­гося ра­диу­са есть не плос­кость, а осо­бая по­верх­ность – пре­дель­ная сфе­ра, или ори­сфе­ра; за­ме­ча­тель­но, что на ней име­ет ме­сто евк­ли­до­ва гео­мет­рия. Это по­слу­жи­ло Ло­ба­чев­ско­му ос­но­вой для вы­во­да фор­мул три­го­но­мет­рии.

8) Дли­на ок­руж­но­сти не про­пор­цио­наль­на ра­диу­су, а рас­тёт бы­ст­рее, чем ра­ди­ус.

9) Чем мень­ше об­ласть в про­стран­ст­ве или на плос­ко­сти Ло­ба­чев­ско­го, тем мень­ше мет­рические со­от­но­ше­ния в этой об­лас­ти от­ли­ча­ют­ся от со­от­но­ше­ний евк­ли­до­вой гео­мет­рии. Например, чем мень­ше тре­уголь­ник, тем мень­ше сум­ма его уг­лов от­ли­ча­ет­ся от π, чем мень­ше ок­руж­ность, тем мень­ше от­но­ше­ние её дли­ны к ра­диу­су от­ли­ча­ет­ся от 2π, и т. п. Умень­ше­ние об­лас­ти фор­маль­но рав­но­силь­но уве­ли­че­нию еди­ни­цы дли­ны, по­это­му при без­гра­нич­ном уве­ли­че­нии еди­ни­цы дли­ны фор­му­лы Л. г. пе­ре­хо­дят в фор­му­лы евк­ли­до­вой гео­мет­рии. Евк­ли­до­ва гео­мет­рия есть в этом смыс­ле «пре­дель­ный» слу­чай гео­мет­рии Ло­ба­чев­ско­го.

В следующих параграф подробнее рассмотрим модели Пуанкаре плоскости Лобачевского

1.2 Модель Пуанкаре плоскости Лобачевского. Точки и прямые. Первая группа аксиом
Евклидова плоскость σ у нас уже построена (будем называть ее Е-плоскостью). Ее точки будем называть Е-точками, а ее прямые – Е-прямыми. Говоря об отношениях на евклидовой плоскости мы тоже будем добавлять букву Е. Возьмем на Е-плоскости σ Е-прямую s. Назовем ее абсолютом. Эта Е-прямая делит плоскость σ на две Е-полуплоскости. Договоримся рисовать Е-прямую s горизонтально. Тогда эти полуплоскости условно назовем верхней и нижней. Рассмотрим верхнюю Е-полуплоскость. Обозначим ее Λ. Будем называть Е-полуплоскость Λ плоскостью в геометрии Лобачевского, короче, плоскостью. Будем называть Е-полуплоскость Λ плоскостью в геометрии Лобачевского, короче, плоскостью. (У нас будет только одна плоскость, так как мы ограничимся построением планиметрии Лобачевского). Точки Е-полуплоскости Λ будем называть точками в геометрии Лобачевского, короче, точками. Прямыми в геометрии Лобачевского, короче, прямыми, будем называть перпендикулярные ему Е-лучи с началом на абсолюте и Е-полуокружности Е-окружностей с центрами на абсолюте.

Аксиома 1: Каковы бы ни были две различные точки A и B, существует единственная прямая, которой они принадлежат.

Доказательство 1: Возьмем две произвольные различные точки A и B. Е-точки A и B могут располагаться двумя разными способами: Е-прямая AB перпендикулярна Е-прямой s и Е-прямая AB не перпендикулярна Е-прямой s. Если Е-прямая AB перпендикулярна Е-прямой s, то проводим ее и берем луч, лежащий в Λ. Если не перпендикулярна, то проводим серединный перпендикуляр к Е-отрезку AB и выходим на центр O Е-окружности. Берем нужную полуокружность. Единственность прямой AB следует из однозначной определенности Е-луча и Е-окружности с центром на s, проходящей через две заданные точки.
1.3 Модель Пуанкаре плоскости Лобачевского. Вторая группа аксиом
Будем говорить, что точка B лежит между точками A и C на прямой a, если

1) (a – Е-луч) Е-точка B лежит между Е-точками A и C;

2) (a – Е-полуокружность с центром O) Е-луч OB является внутренним лучом Е-угла AOC. Будем в этом случае обозначать A−B −C.

II₁. Если A−B−C, то A, B и C – три различные точки прямой и C −B − A.

Выполнение этой аксиомы непосредственно следует из свойств углов и внутренних лучей евклидовой геометрии.

II₂. Каковы бы ни были две точки A и B, существует по крайней мере еще одна точка C на прямой AB, такая, что A−B − C.

Выполнение этой аксиомы тоже непосредственно следует из свойств фигур в евклидовой геометрии.

II₃. Среди трех точек одной прямой существует не более одной, лежащей между двумя другими.

Для случая Е-луча утверждение следует из этой же аксиомы для евклидовой геометрии. В случае Е-угла легко показать, что если Е-луч OB является внутренним Е-лучом Е-угла AOC, то Е-луч OA не является внутренним Е-лучом Е-угла BOC. И тоже самое для OC.

II₄. Пусть A, B, C – три точки, не лежащие на одной прямой и a – прямая, лежащая в плоскости ABC, не проходящая ни через одну из точек A, B, C. Тогда если прямая a проходит через точку отрезка AB, то она проходит через точку отрезка AC или BC.

1.4 Модель Пуанкаре плоскости Лобачевского. Третья группа аксиом
Рассмотрим евклидову плоскость σ. Фиксируем на ней точку O и окружность ω радиуса R с центром в этой точке. Отображение множества σ \ O на себя, которое каждой точке M ставит в соответствие точку M₀, такую, что

1) M₀ ∈ [OM];

2) OM · OM₀ = R².

Образ точки M строится следующим образом:

1) если точка внутри окружности. Строим луч OM. Через точку пересечения с окружностью проводим касательную к ней. Пересекаем касательную с лучом OM. Получаем точку M₀.

2) если точка вне окружности. Строим луч OM. Через M проводим касательные к окружности. Соединяем точки касания A и B. Пересечение прямой AB и луча OM – искомая точка M₀.

Замечание. Напомним еще одно свойство инверсии, которое помогает строить образы точек. Пусть инверсия I с центром O переводит точку A в A₀, B в B₀. Тогда ∠OBA = ∠OA₀B₀. При этом говорят, что прямые AB и A0B0 антипараллельны.

Посмотрим, что будет происходить с прямыми и окружностями при инверсии. Проще всего для исследования инверсии подходят комплексные числа. Напомним, что комплексное число z – это упорядоченная пара вещественных чисел (x, y). Алгебраическая запись комплексного числа z = x+iy. Комплексное число x−iy называется сопряженным и обозначается z¯. Если на плоскости зафиксировать прямоугольную декартову систему координат, то комплексное число можно изобразить точкой плоскости с координатами (x, y) А можем изобразить представителем вектора с координатами (x, y), отложенного от начала системы координат. Сумму комплексных чисел можем представить как сумму векторов, умножение на вещественное число – как умножение вектора на вещественное число. Модуль |z| определяется так:

|z| ² = x ² + y ² = zz¯

является длиной вектора, изображающего число z. Используя эти свойства комплексных чисел выведем формулу для инверсии в комплексных числах. Пусть дана окружность радиуса R с центром O. Выберем прямоугольную декартову систему координат с началом в точке O. Точка M(x, y) будет задаваться комплексным числом z = x + iy. Точка M0 (x₀ , y₀ ) (ее образ при инверсии) будет задаваться комплексным числом z 0 . Тогда z 0 = λz, где λ – некоторое положительное вещественное число, которое нужно найти. Мы знаем из определения инверсии, что OM · OM0 = R². Длина отрезка OM – это модуль комплексного числа z, а длина отрезка OM0 – это модуль комплексного числа z₀. Тогда получим |z||z₀ | = R². Подставляем z₀ = λz и учитываем, что |λz| = λ|z| (очевидное равенство, если представлять комплексные числа как векторы и учесть положительность λ).

Тогда

λ|z|² = R ² ⇔ λzz¯ = R² ⇔ λ = R² zz¯.

Подставляем найденное λ в z₀ = λz, сокращаем на z и получаем формулу инверсии в удобной системе координат (центр системы в центре окружности инверсии) z₀ = R² z¯.

Теорема 2. Пусть окружность ω1 с центром Q1 радиуса r1 переходит в окружность ω 0 с центром Q2 радиуса r2 при инверсии I. Тогда центр инверсии O будет центром гомотетии этих окружностей.

Доказательство 2. Расположим систему координат так, чтобы начало совпадало с центром инверсии, а ось Ox совпадала с прямой, соединяющей центры окружностей. Тогда центры окружностей будут задаваться вещественными числами и мы получим ω1 :

zz¯ + az + az¯ + b = 0; z0 = R² z¯ .

Находим образ окружности ω1 при инверсии

zz¯ + aR² b z + aR² b z¯ + R⁴ b = 0.

Точно такая же должна получиться окружность при гомотетии с некоторым коэффициентом k и тем же центром: z 0 = kz.

Получаем

k ² zz¯ + akz + akz¯ + b = 0.

Так как эти уравнения должны задавать одну и ту же окружность, получаем

ak/k ² = aR²/b

b /k ² = R⁴ b .

Откуда получаем, что при гомотетии с коэффициентом k = bR² мы получим то, что хотели.

1.5 Модель Пуанкаре плоскости Лобачевского. Четвертая группа аксиом
Эта группа аксиом состоит из двух аксиом: Архимеда и Кантора.

IV₁. (аксиома Архимеда) Пусть AB и CD – какие-нибудь отрезки. Тогда на прямой AB существует конечное множество точек A1, A2, . . . , An−1, An, таких, что выполняются условия:

а) A − A₁ − A₂, A₁ − A₂ − A₃, . . . , A_n−2 − A_n−1 − A_n; б) AA₁ = A₁A₂ = . . . = A_n−1A_n = CD;

в)A−B − An.

IV₂. (аксиома Кантора) Пусть на произвольной прямой a дана бесконечная последовательность отрезков A1B1, A2B2, . . . , из которых каждый последующий лежит внутри предыдущего и, кроме того, для любого отрезка CD найдется натуральное число n, такое, что AnBn < CD. Тогда на прямой a существует точка M , принадлежащая каждому из отрезков данной последовательности. Говорят, что установлено измерение отрезков, если определено отображение l : L → R+ из множества всех отрезков в множество положительных вещественных чисел, которое удовлетворяет условиям:
1) если отрезки AB и A′B′ конгруэнтны, то l(AB) = l(A′B′);
2) если A−B − C, то l(AB) + l(BC) = l(AC);
3) существует отрезок PQ, такой, что l(PQ) = 1
1.6 Модель Пуанкаре плоскости Лобачевского. Пятая группа аксиом
Пятая группа аксиом состоит из одной аксиомы – аксиомы Лобачевского.

V ∗. Через точку, не лежащую на данной прямой проходит более одной прямой, не пересекающей данную.

Проиллюстрируем, что эта аксиома выполняется в модели Пуанкаре плоскости Лобачевского.На рисунке изображено несколько прямых, проходящих через точку A и не пересекающих прямую a. Следовательно, аксиома Лобачевского в модели Пуанкаре выполняется. Обратите внимание на прямые b и e. Они выделяются среди других прямых, не пересекающих прямую a. Эти прямые называются параллельными прямой a. Дадим строгое определение параллельных прямых на плоскости Лобачевского.

Сначала вспомним определение направления на прямой. Рассмотрим на прямой множество всех лучей. На этом множестве задается отношение эквивалентности: два луча h и k называются сонаправленными, если либо

h ⊂ k, либо k ⊂ h. В противном случае лучи называются противоположно направленными. Это отношение разбивает все лучи прямой на два класса эквивалентности: в каждом классе лежат сонаправленные между собой лучи, а лучи разных классов противоположно направленные. Каждый из этих классов называется направлением на прямой. Обозначать направленные прямые будем также, например AB, а направление будем

считать от первой буквы ко второй. Будем говорить, что направленные прямые AB и CD параллельны (в направлении точек B

и D), если

1) эти прямые не пересекаются,

2) для любой точки P на прямой AB и любой точки

Q на прямой CD любой внутренний луч PK угла QPB пересекает луч QD.
1.7 Треугольники и четырехугольники на плоскости Лобачевского
Пусть даны четыре точки A, B, C, D, никакие три из которых не лежат на одной прямой, и четыре отрезка AB, BC, CD, AD, попарно не имеющие общих внутренних точек. Четырехугольник ABCD называется двупрямоугольником, если он имеет два прямых угла A и B. Сторона AB называется основанием двупрямоугольника. Четырехугольник ABCD называется трипрямоугольником или четырехугольником Ламберта, если он имеет три прямых угла.

Замечание 2. Если в качестве пятой группы аксиом взять аксиому Евклида, то двупрямоугольник будет трапецией с прямыми углами при основаниях, в частности, будет прямоугольником. Четырехугольник Ламберта будет прямоугольником. Если в качестве пятой группы аксиом взять аксиому Лобачевского, то двупрямоугольник и четырехугольник Ламберта будут иметь ряд свойств, отличных от свойств прямоугольников на евклидовой плоскости. Четырехугольником Саккери называется двупрямоугольник, у которого стороны, прилегающие к прямым углам равны.
1.8 Окружность, орицикл, эквидистанта в модели Пуанкаре плоскости Лобачевского
Окружность. Окружность Ω в плоскости Лобачевского определяется также как и на евклидовой плоскости. Окружностью называется множество точек плоскости Лобачевского, находящихся на данном расстоянии от данной точки. Эта точка называется центром.

Расстояние мы можем задать с помощью отрезка P Q. Тогда для построения точек окружности Ω нужно взять точку O (центр окружности), провести прямую через эту точку и отложить от точки O на этой прямой в обе стороны отрезки, конгруэнтные P Q. Проводим еще одну прямую через точку O и опять откладываем отрезки, конгруэнтные P Q.

Еще один способ построения точек окружности Ω основан на следующем свойстве окружности: любая прямая, проходящая через центр окружности, является ее осью симметрии. Другими словами, если взять на окружности произвольную точку A, провести через центр окружности O прямую и отразить точку A от этой прямой, то мы попадем опять на окружность. Вспоминаем, что осевая симметрия на модели Пуанкаре – это инверсия. Значит, чтобы построить точки окружности, нужно взять точку O – центр окружности, взять точку A, такую, что отрезок OA равен радиусу окружности, провести через точку O прямую Q (Е-дугу с центром на абсолюте) и построить образ точки A при инверсии относительно Е-окружности Q.

В результате получим еще одну точку данной окружности. (Посмотрите динамический рисунок Окружность, эквидистанта, орицикл.) Возникает вопрос: какой линией евклидовой плоскости изображается окружность в модели Пуанкаре плоскости Лобачевского. 33 Возьмем точку O – центр окружности Ω и точку A, так, чтобы они лежали на Е-луче (удобно задаем себе радиус окружности с помощью отрезка OA). Сначала построим диаметрально противоположную точку B. Для этого нам потребуется Е-окружность Q, проходящая через точку O с центром в точке пересечения Е-луча OA и абсолюта. Строим стандартным образом образ точки A при этой инверсии. Для построения произвольной точки M искомой окружности будем двигать точку C по абсолюту, проводить Е-окружности с центром в точке C и проходящие через точку O, и находить образы точки A относительно этих инверсий.

Мы видим, что получается линия, похожая на Е-окружность, но центр у нее не в точке O. Докажем это аналитически. Введем систему координат как показано на рисунке. Точки A и O лежат на оси y, то есть на мнимой оси, а значит им соответствую чисто мнимые числа, которые мы обозначим O(ai), A(bi). Найдем, какое комплексное число соответствует точке B. Она является образом точки A при инверсии относительно Е-окружности Q. Формула этой инверсии имеет вид z ₀ = a ² z¯ (очевидно, что радиус Е-окружности Q равен a). Тогда точке B сопоставляется чисто мнимое число a ² −bi = a ² b i. Инверсия относительно Е-окружности ω с центром в точке C(c) будет иметь формулу

z ₀ = |c − ai| ² z¯ − c + c = c ² + a ² z¯ − c + c.

Тогда точке M (образ точки A при инверсии относительно Е-окружности ω) будет соответствовать комплексное число

z = a ² + c ² −bi − c + c.

Окружность ω будет меняться, следовательно, будет меняться число c и за ним следом будет меняться число z. Получаем множество точек M. Множество всех точек M и образует искомую 34 нами окружность (в смысле Лобачевского). Мы подозреваем, что это множество изображается Е-окружностью с диаметром AB и радиусом AB 2 (в смысле Евклида). Центр этой Е-окружности будет в точке, которой соответствует комплексное число bi + a ² b i ² = a ² + b ² 2b i. Радиус этой Е-окружности будет b − a ²+b ² 2b = b ² − a ² 2b . Уравнение такой Е-окружности в комплексных числах имеет вид (z − a 2 + b ² 2b i)(¯z + a ² + b ² 2b i) = b ² − a ² 2b Чтобы проверить принадлежность точки M этой Е-окружности, нужно убедиться, что соответствующее ей комплексное число удовлетворяет этому уравнению.

Подставляем в левую часть уравнения комплексное число, соответствующее M и преобразовываем полученное выражение. Должны получить то, что стоит справа в (8.1). a 2 + c 2 −c − bi + c − a 2 + b 2 2b i a ² + c 2 −c + bi + c + a 2 + b 2 2b i = Преобразуем первую скобку, вторая будет ей комплексно сопряжена и получится автоматически. a² + c ² −c − bi + c − a ² + b² 2b i = a 2 c − b² c − a² bi − bc² i −(b² + c² ) − a² + b² 2b i =

= 2bc(a² − b 2 ) + (a² − b² )(c 2 − b 2 )i −2b(b 2 + c 2 ) = (a² − b² ) −2b(b² + c² ) (2bc + (c 2 − b 2 )i). Возвращаемся к прерванной цепочке равенств = (a² − b² ) −2b(b 2 + c 2 ) 2 (4b 2 c 2 + (c 2 − b 2 ) 2 ) = b ² − a ² 2b. Мы получили то, что ожидали.

Таким образом, мы показали, что все точки окружности Ω лежат на Е-окружности. Можно показать, что любая точка этой Е-окружности будет точкой окружности Ω. Итак, мы получили, что окружность Ω в модели Пуанкаре плоскости Лобачевского изображается Еокружностью, но центры их не совпадают.

Орицикл. Секущей равного наклона двух прямых a и b на плоскости Лобачевского называется прямая c, которая при пересечении с ними образует равные односторонние углы. Пусть дано семейство направленных прямых, любые две из которых параллельны. Будем говорить, что точки A и B плоскости Лобачевского находятся в отношении ∆, если прямая AB является секущей равного наклона к прямым данного семейства, проходящим через точки A и B.

Отношение ∆ является отношением эквивалентности. Множество всех точек плоскости Лобачевского разбивается на классы эквивалентности по этому отношению. Каждый из классов называется орициклом. В курсе геометрии Лобачевского бакалавриата было доказано, что любая прямая из семейства параллельных прямых, задающих орицикл, является его осью симметрии.

Другими словами, если взять точку на орицикле и отобразить ее осевой симметрией с осью из данного пучка параллельных прямых, то попадем опять на тот же орицикл. Используя это свойство, можно построить точки орицикла.

Рассмотрим пучок параллельных прямых. На рисунке изображены две такие прямые – это Е-луч и Е-дуга Q, проходящие через точку B. Возьмем точку A (может быть выбрана произвольно на плоскости Лобачевского). Построим еще одну точку, принадлежащую орициклу, который проходит через A. Строим точку M – образ точки A при инверсии относительно окружности Q. Это будет точка орицикла. Двигаем точку C – центр окружности Q – вдоль абсолюта и строим относительно получающихся окружностей образы точки A. Это будут точки орицикла.

Построив несколько точек, мы можем выдвинуть гипотезу, что орицикл в модели Пуанкаре изображается окружностью. Докажем это. Так как Е-прямая AB является касательной к любой окружности Q, красная пунктирная окружность (построена на AC как на диаметре) всегда проходит через точку B. Из алгоритма построения образа точки при инверсии следует, что AM перпендикулярно BM.

Следовательно, угол AMB прямой и точка M является точкой окружности с диаметром AB. Можно показать и обратное, что любая точка Е-окружности с диаметром AB является образом точки A относительно некоторой окружности Q, то есть будет точкой орицикла (рис.1).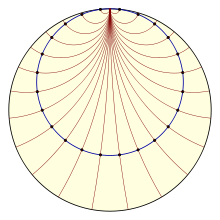

Рисунок 1 – Орицикл в модели Пуанкаре
Эквидистанта. Пусть на плоскости Лобачевского дана прямая a и отрезок MN. Множество точек, принадлежащих одной полуплоскости относительно a и находящихся на расстоянии MN от нее, называется эквидистантой. Прямая a называется базой эквидистанты. Другими словами, эквидистанта – это множество точек плоскости, которое получается следующим образом: через каждую точку базы проводим прямую, перпендикулярную ей, и откладываем на этой прямой отрезок, равный MN.
1.9 Замечательные точки и замечательные прямые треугольника на плоскости Лобачевского в модели Пуанкаре
Замечательными прямыми треугольника называются прямые, содержащие биссектрисы, высоты, медианы треугольника, а также прямые, содержащие биссектрисы внешних углов треугольника, и серединные перпендикуляры к сторонам треугольника. Точки пересечения соответствующих групп замечательных прямых называются замечательными точками треугольника.

Биссектриса треугольника является объектом абсолютной геометрии (то есть геометрии, построенной на первых четырех группах аксиом). Понятие биссектрисы угла вводится в третьей группе аксиом. Теорема о пересечении биссектрис треугольника в одной точке также является теоремой абсолютной геометрии. Она также доказывается в третьей группе аксиом. Значит, эта теорема верна и в геометрии Лобачевского.

Медиана треугольника является объектом абсолютной геометрии. Она определяется в третьей группе аксиом (для нее нужно понятие конгруэнтности отрезков, сам треугольник возникает уже во второй группе аксиом). Теорема о пересечении медиан треугольника в одной точке в евклидовой геометрии доказывается с помощью подобия, то есть для ее доказательства существенен пятый постулат Евклида. Но, оказывается эта теорема верна также и в геометрии Лобачевского.

Понятие серединного перпендикуляра также как и понятия медианы и биссектрисы вводится в третьей группе аксиом. Но в отличие от них серединные перпендикуляры треугольника в геометрии Лобачевского не обязательно пересекаются в одной точке. Доказывается, что серединные перпендикуляры к сторонам треугольника принадлежат к одному пучку прямых, то есть либо все три пересекаются в одной точке, либо все три параллельны, либо все три расходятся.

Глава 2 – Решение задач
На основании теоретических аспектов стереометрии Лобачевского, рассмотрим некоторые задачи:

Задача 1

Докажите, что окружность ω, проходящая через две инверсные точки (то есть соответствующие друг другу при инверсии) является инвариантной.

Решение. Зададим инверсию в хорошей системе координат, в которой центр инверсии и начало системы координат совпадают. Тогда формулы инверсии будут иметь вид z₀ = R² z¯ . Ось Ox системы координат выберем так, чтобы она проходила через центр данной окружности ω. Тогда уравнение окружности будет иметь вид (z − z0)(¯z − z0) = r ² , где z₀ – комплексная координата центра данной окружности ω. Она будет вещественным числом, следовательно z¯₀ = z₀. Возьмем не инвариантную точку w с данной окружности. По условию этой окружности принадлежит и образ этой точки. Тогда мы получаем два верных равенства

(w − z₀)( ¯w − z₀) = r ² ; ( R² w¯ − z0)(R² w − z₀ ) = r ² .

Раскроем скобки и перенесем все слагаемые в одну часть ( ww¯ − z₀w¯ − z₀w + z₀z₀ − r ² = 0 −r²ww¯ − R²wz0 − R²wz¯ 0 + R⁴ + ww¯(z₀) ² = 0. Избавимся от средних слагаемых. Для этого домножим первое равенство на −R² и сложим со вторым.

((z₀) ² − R ² − r ² )ww¯ − R ² ((z0) 2 − R ² − r ² ) = 0.

Так как мы брали точку w не инвариантную, она не может лежать на окружности инверсии, следовательно, не удовлетворяет ее уравнению, то есть ww¯ = R² . Следовательно,

(z₀)² = R² + r² .

Это условие ортогональности данной окружности и окружности инверсии. Следовательно, данная окружность ω будет инвариантной относительно инверсии.

Задача 2

Найдите инверсию, переводящую данную прямую в данную окружность.

Решение. Пусть даны прямая ` и окружность ω. Как мы знаем, прямая, соединяющая центр инверсии и центр окружности ω, перпендикулярна прямой `. Кроме того, окружность ω проходит через центр инверсии. Из этого строим точку O – центр инверсии. Так как соответствующие при инверсии точки лежат на одном луче с точкой O, мы получаем две соответствующие точки M и M₀ . Радиус окружности инверсии будет выглядеть так:

R = √ (OM · OM₀ ).
Задача 3

Пусть дан отрезок AB. Постройте его середину C.

Решение. Рассмотрим случай, когда отрезок AB располагается на Е-окружности ω. Случай, когда отрезок AB располагается на Е-луче, рассмотрите самостоятельно. Как и на евклидовой плоскости, задачи на построение на модели плоскости Лобачевского начинаются с анализа. Пусть точка C построена. Тогда отрезок AC конгруэнтен отрезку CB. Следовательно, должна существовать последовательность инверсий, переводящая отрезок AC в отрезок CB. Смотрим, нельзя ли обойтись одной инверсией. Точка C должна переходить в себя (то есть являться инвариантной), а точка A должна переходить в точку B. Рассмотрим инверсию I, для которой точки A и B соответствуют друг другу. Тогда окружность, содержащая эти точки перейдет в себя, а ее точка пересечения с окружностью инверсии будет инвариантной. Это и будет точка C. Следовательно, нам нужно построить окружность инверсии, для которой точка A переходит в точку B, а ее центр лежит на абсолюте. Центр инверсии O получается как пересечение Е-прямой AB и абсолюта. Далее, так как Е-окружность ω инвариантна, она ортогональна окружности инверсии. Как мы видели в теме инверсия, это означает, что радиус каждой из этих Е-окружностей будет касательной к другой из них. Значит, нам нужно из точки O провести касательную к окружности ω. Напомним, что в третьей группе аксиом вводится понятие прямого угла. Угол называется прямым, если он конгруэнтен смежному. Две прямые называются перпендикулярными, если они образую прямой угол
Задача 4

Докажите, что инверсия моделирует осевую симметрию.

Решение. Пусть дана прямая a. Преобразование плоскости, которое каждой точке M ∈ a ставит в соответствие ее же, а каждой точке M ∈ a ставит в соответствие точку M₀ , такую, что MM₀ ⊥ a и середина отрезка MM₀ ∈a. Рассмотрим прямую a на модели и точку M ∈ a. Тогда при инверсии с Е-окружностью a точка M будет инвариантной, то есть перейдет в себя. Пусть M∈ a. При инверсии она перейдет в точку M₀ , такую, что Е-окружность b с центром на абсолюте, проходящая через точки M и M₀ будет инвариантной. Эта Е-окружность является прямой MM₀ , которая перпендикулярна a. Кроме того, точка A пересечения Е-окружности a и Е-окружности b будет инвариантной. Тогда при инверсии отрезок MA перейдет в отрезок M₀A, то есть A является серединой отрезка MM₀ .

Задача 5

Изобразите две пересекающиеся прямые и их заградительные прямые в модели Пуанкаре плоскости Лобачевского.

Решение. Такая заградительная прямая единственная. Для параллельных прямых каждая из трех прямых a, b, c является заградительной для двух других прямых.


Заключение
Таким образом, в ходе написания работы мы показали модели в стереометрии Лобачевского. Привели некоторые примеры задач. Рассмотрели теоремы и их доказательства. Аксиоматический метод и аксиоматические исследования Лобачевского сыграли огромную роль в развитии геометрии как науки, а также нашли свое отражение и в теории познания, т.е. переоценить их значение невозможно.

Стереометрия Лобачевского представляет теорию, богатую содержанием и имеющую применение как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики.

Стереометрия Лобачевского продолжает разрабатываться многими математиками; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и т. п. Ряд математиков развивали также механику в пространстве Лобачевского. Эти исследования не нашли непосредственных применений в механике, но дали начало плодотворным геометрическим идеям.

В целом геометрия Лобачевского является обширной областью исследования, подобно геометрии Евклида.


Список литературы
1. Атанасян Л.С., Базылев В.Т. Геометрия, Том 2, Москва, Просвещение, 1988.

2. Иовлев Н.Н., Введение в элементарную геометрию и тригонометрию Лобачевского, Москва, 1930;

3. Каган В. Ф., Лобачевский и его геометрия. Общедоступные очерки, М., 1955;

4. Клейн Ф.К. Неевклидова геометрия, пер.Брушлинского Н.К., М - Л, 1936;

5. .Мищенко А.С., А.Т. Фоменко Курс дифференциальной геометрии и топологии, Москва, 2000.

6. Погорелов А. В., Основания геометрии, 3 изд., М., 1968;

7. Подаева Н.Г., Жук Д.А Лекции по основам геометрии - Елец.: ЕГУ, 2005. - 62с.

8. Прасолов В.В., Геометрия Лобачевского, Издание третье исправленное и дополненное, МЦНМО, 2004;

9. Смогоржевский А.С., О геометрии Лобачевского, Государственное издательство технико - теоретической литературы, выпуск 23, Москва, 1957;

10. Широков П. А., Краткий очерк основ геометрии Лобачевского, М., 1955;

11. Яглом И.М., Геометрические преобразования II том. Под ред. Э.П.Тихонова, Москва, 1956;.