лаб. Основные формулы

• Название: Основные формулы
• Дата: 26.04.2023
• Размер: 392 Kb.
• Имя файла: zadachi_dlya_samresheniya.doc
• Тип: Закон; #1090566

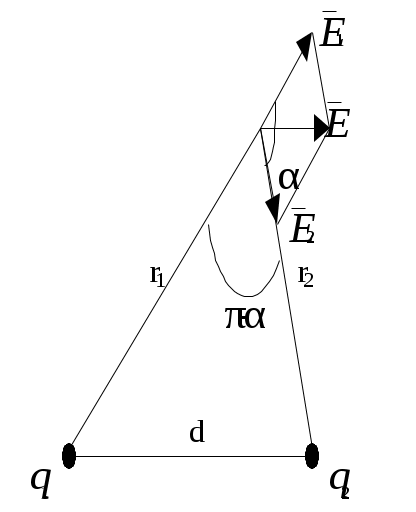
Основные формулы

1.Электростатическое поле в вакууме.
1.1.Закон Кулона

,или

где F – сила взаимодействия между двумя точечными зарядами q₁ и q₂ в вакууме; ε₀=8,85·10^-12 Ф/м – электрическая постоянная; k=9·10⁹ м/Ф, r - расстояние между зарядами.

1.2.Закон сохранения заряда

-

алгебраическая сумма зарядов тел, образующих изолиро-ванную систему, равна нулю.

1.3.Напряженность электрического поля

,

где - сила, действующая на точечный пробный заряд ,

помещенный в данную точку поля.

1.4.Потенциал электрического поля

,

где W – потенциальная энергия точечного пробного заряда

, помещенного в данную точку поля.

1.5.Работа сил по перемещению заряда из точки поля с потенциалом φ₁в точку с потенциалом φ₂

A=q·(φ₁-φ₂)=q·U,

где U – разность потенциалов электрического поля в начальной и конечной точках.

1.6.Напряженность Е и потенциал φ поля точечного заряда

,

1.7.Напряженность и потен­циал φ связаны между собой соотношением:

или

1.8.Принцип суперпозиции (наложения) полей

,

,

где - напряженность, φ – потенциал поля, созданного

системой зарядов.

1.9.Теорема Остроградского-Гаусса: поток вектора напряженности 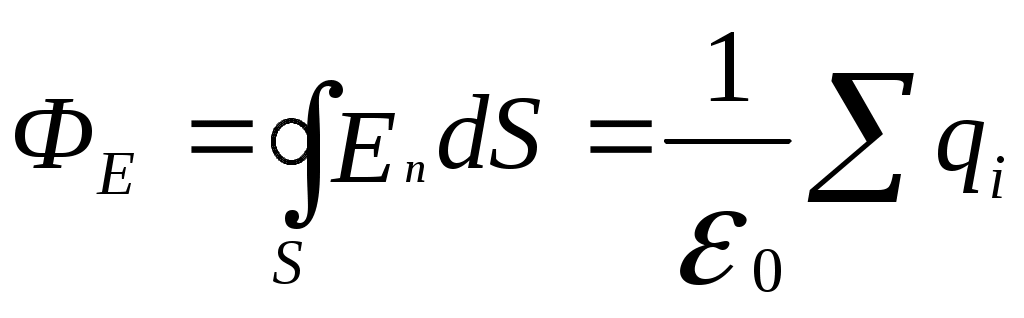через произвольную замкнутую поверхность S равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε₀,

.

1.10.Напряженность электрического поля, создаваемого проводящей сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:

а) внутри сферы (r < R) E = 0;

б) на поверхности сферы (r = R)

в) вне сферы (r > R)

1.11.Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси

,

где -линейная плотность заряда нити (цилиндра).

1.12.Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью

,

где - поверхностная плотность заряда плоскости.

1.13.Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями с одинаковой по модулю поверхностной плотностью заряда (поле плоского конденсатора):


2. Диэлектрики в электрическом поле
2.1.Индукция электрического поля (электрическое смещение)

,

где - поляризованность диэлектрика.

2.2.Теорема Остроградского-Гаусса для индукции электрического поля (электрического смещения):

,

где -алгебраическая сумма свободных зарядов, находящихся внутри поверхности S.

2.3.Напряженность электрического поля в диэлектрике и поляризованность диэлектрика связаны соотношением

=ε₀ (ε-1)

где ε=Е₀/Е диэлектрическая проницаемость диэлектрика.

2.4. Связь индукции и напряженности электрического поля

2.5.Связь напряженности электрического поля в диэлектрике с напряженностью поля свободных и связанных зарядов



2.6.Поверхностная плотность связанных зарядов



где Р_n и E_n - нормальные составляющие поляризованноcти диэлектрика и напряженности электрического поля.
3. Проводники в электростатическом поле.
3.1.Условие равновесия зарядов в проводнике:

, φ= const,

где - напряженность электрического поля в произвольной точке внутри проводника, φ – потенциал произвольной точки проводника.

3.2.Электроемкость проводника

С=q/φ,

где q -заряд проводника, φ - потенциал поверхности проводника.

3.3.Электроемкость уединенной проводящей сферы радиуса R

С=4πεε₀R,

где R – радиус сферы, ε-диэлектрическая проницаемость среды, в которой находится проводник.

3.4.Электроемкость конденсатора

С=q/U,

где q – заряд одной из обкладок, U – разность потенциалов между обкладками конденсатора.

3.5. Электроемкость плоского конденсатора

,

где S - площадь одной пластины; d- расстояние между пластинами, ε – диэлектрическая проницаемость диэлектрика, находящегося между пластинами конденсатора.

3.6.Электроемкость батареи конденсаторов

а) при последовательном соединении

;

б) при параллельном соединении

.

3.7.Энергия заряженного конденсатора



3.8.Объемная плотность энергии электрического поля

.
4. Постоянный ток.
4.1.Сила тока I=dq/dt,

где q - заряд прошедший через поперечное сечение за время dt/

4.2.Плотность тока j=I/S, где S - площадь поперечного сечения проводника.

4.3.Связь плотности тока со средней скоростью направ­ленного движения заряженных частиц ,

где е- заряд частицы; n-концентрация заряженных частиц.

4.5.Закон Ома

а) Для участка цепи I=U/R,

где U – напряжение, R - сопротивление участка;

б) для замкнутой цепи

,

где E - э.д.с. источника тока, R – внешнее сопротивление цепи, r- внутреннее сопротивление источника тока.

в) закон Ома в дифференциальной форме



где σ - удельная теплопроводность, - напряженность электрического поля в проводнике.

4.6.Сопротивление однородного проводника постоянного поперечного сечения

,

где ρ - удельное сопротивление; l – длина, S - площадь поперечного сечения проводника.

4.7.Зависимость удельного сопротивления металлов от температуры

,

где ρ₀ – удельное сопротивление металла при t₀=0⁰С, t – температура по шкале Цельсия, α – температурный коэффициент сопротивления.

4.8.Правила Кирхгофа:

а)первое правило: алгебраическая сумма сил токов, сходящихся в узле равна нулю



б)второе правило: в произвольном замкнутом контуре разветвленной электрической цепи алгебраическая сумма произведений сил токов на сопротивления участков ( ) равна алгебраической сум­ме э.д.с. ( ).

.

4.9. Работа и мощность тока





4.10. Закон Джоуля-Ленца dQ=dA.

4.11.Закон Джоуля-Ленца в дифференциальной форме

P_уд= σЕ².
Примеры решения задач.
Пример 1. Два точечных электрических заряда q₁= 1кКл и q₂= -2 кКл находятся в вакууме на расстоянии d= 10 см друг от друга. Определить напряженность Е и потенциал φ поля этих зарядов в точке А, удаленной от заряда q₁ на расстояние r₁=9 см и от заряда q₂ на r₂=7см.

Решение. Согласно принципу суперпозиции электрических полей напряженность электри­ческого поля равна геометри­ческой сумме напряженностей и полей, создаваемых каждым зарядом в отдельности: . Напряженности электрических полей, создаваемых зарядами q₁ и q₂, равны:

; (1)

Вектор (рис. 1) направлен по силовой линии от заряда q₁, так как заряд q₁ положителен; вектор направлен к заряду q₂, так как заряд q₂ отрицателен.

Рис. 1

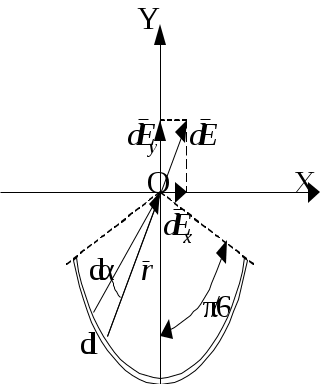
Модуль вектора E найдем по теореме косинусов:

(2)

где α - угол между векторами и , который может быть найден из треугольника со сторонами r₁, r₂, d:

.

Подставляя данные, получаем:



Подставляя выражения E₁ и E₂ из формул (1) в (2), получим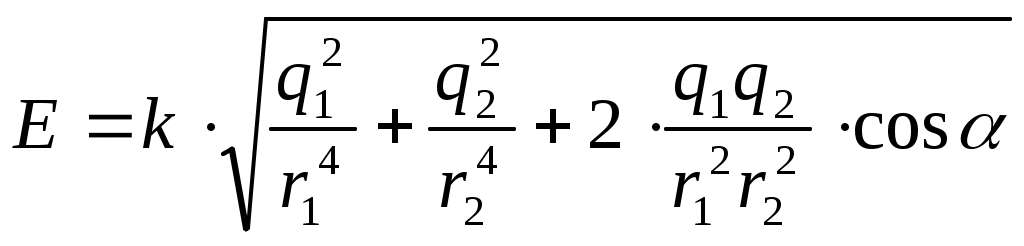

(3)

Подставим значения величин в формулу (3) и произведем вычисления: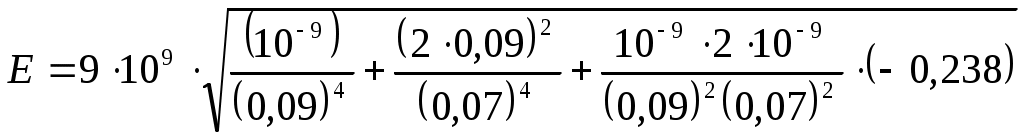

= 3,58·10³ В/м = 3,58 кВ/м.

В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, создаваемого двумя зарядами q₁ и q₂ равен алгебраической сумме потенциалов, т. е.

φ = φ₁ + φ₂ (4)

Потенциал электрического поля, создаваемого в вакууме точечным зарядом q на расстоянии r от него, выражается формулой

(5)

Согласно формулам (4) и (5) получим

,или .

Подставив в это выражение значения физических величин, получим


Пример 2. Точечный заряд q = 25·10^-9 Кл находятся в поле, создаваемом прямым бесконечным цилиндром радиусом

R=10^-2м, равномерно заряженным с поверхностной плотностью заряда σ =25·10^-6 Кл/м². Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r= 0,1 м.

Решение. Сила, действующая на заряд q, находящийся в электрическом поле поле

F= qE (1)

где E - напряженность поля в точке, в которой находится заряд. Напряженность поля бесконечно длинного равномерно заряженного цилиндра равна

(2)

Выразим линейную плотность заряда τ через поверхностную плотность σ. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд q₁ двумя способами:

q₁ = σS =σ2πRl и q₁ = τl.

Приравняв прямые части этих равенств, получим

τl = 2πRlσ  τ = 2πRσ

С учетом этого формула (2) примет вид

Подставив это выражение E в формулу (2) получим искомую силу:

(3)

F =25 ·10^-9· 2· 10^-6 ·10^-2/(8,85· 10^-12 ·1·0 10^-12) = 565 ·10^-6 Н

Направление силы совпадает с направлением вектора , а последний в силу симметрии направлен перпендикулярно цилиндру.
Примеp 3. По тонкой нити, изогнутойпо дуге окружности, равномерно распределен заряд с линейной плотностью τ=10нКл/м. Определить напряженность Е и потенциал φэлектрического поля, создаваемого таким распределенным зарядом в точке, совпадавшей с центром кривизны дуги. Длина нити l составляет одну треть длины окружности и равна 15 см.

Решение. Выберем оси координат X и Y так, чтобы начало координат совпадало с центром кривизны дуги, а ось Y была бы симметрично расположена, относительно концов дуги (рис.2). Выделим элемент нити длиной dl.

Рис.2.

Заряд dq =τ·dl, находя­щийся на выделенном участке, можно считать точеч-ным.

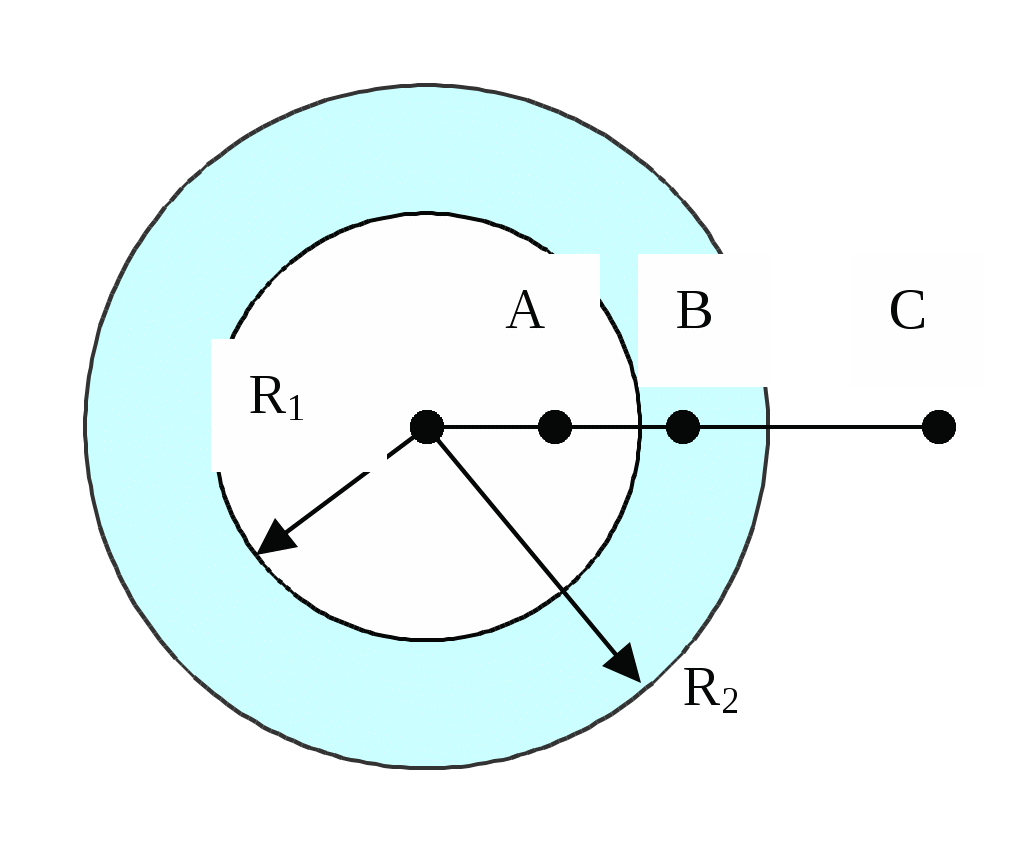
Определим на-пряженность электрического поля в точке О. Для этого, най-дем напряжен-ность поля, создаваемого зарядом dq:

,

где - радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность.

Напряженность поля, создаваемого всей нитью в соответствии с принципом суперпозиции равна



Интегрирование ведется вдоль дуги, образованной нитью.

Выразим вектор через составляющие и на оси координат:



Тогда



В силу симметрии интеграл равен нулю, тогда

, или , (1)

где .
Так как r=const, dl=rdα, то


Отсюда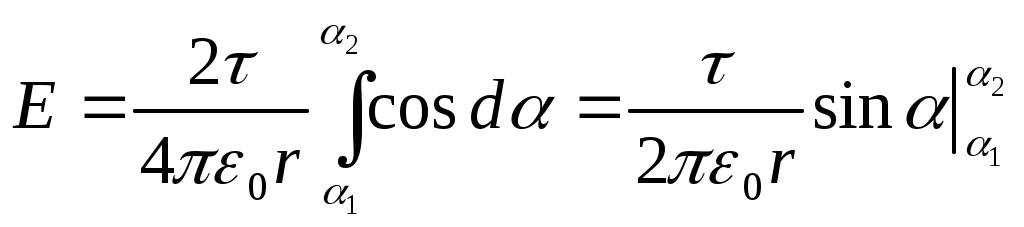



Здесь принято во внимание симметричное расположение дуги относительно оси У, и поэтому интегрирование проводится по половине дуги (от α₁=0 до α₂=π/6) а ре­зультат удваивается.

Подставив пределы и выразив через длину дуги (3·l=2πr), получим



Подставим значение τ и l в полученную формулу и вычислим:



Найдем потенциал электрического поля вточке. Сначала найдем потенциал dφ , создаваемый точечным зарядом dQв точке O:



Интегрируя, получим:



Так как l=2 πr/3, то

Произведем вычисления:

В.
Пример 4. Два бесконечных тонкостенных коаксиальных цилиндра радиусами R₁=5см и R₂=10см равномерно заряжены с поверхностными плотностями зарядов равными, соответственно, σ₁=10^-8Кл/м² и σ₂= -3·10^-8 Кл/м² (рис.3). Пространство между цилиндрами заполнено парафином (ε=2). Определить напряженность поля в точках, находящихся на расстояниях: r₁=2 см; r₂=6см; r₃=15 см от оси цилиндра.

Решение. Воспользуемся теоремой Остроградского-Гаусса для индукции электрического поля и связью индукции и напряженности электрического поля:

, .

Рис.3

Легко видеть, что индукция в точке А (на расстоянии r₁=2 см от оси) равна 0 (заряды внут-ри цилин-дрической поверхности S₁, проходя-щей через точку А, отсутствуют).

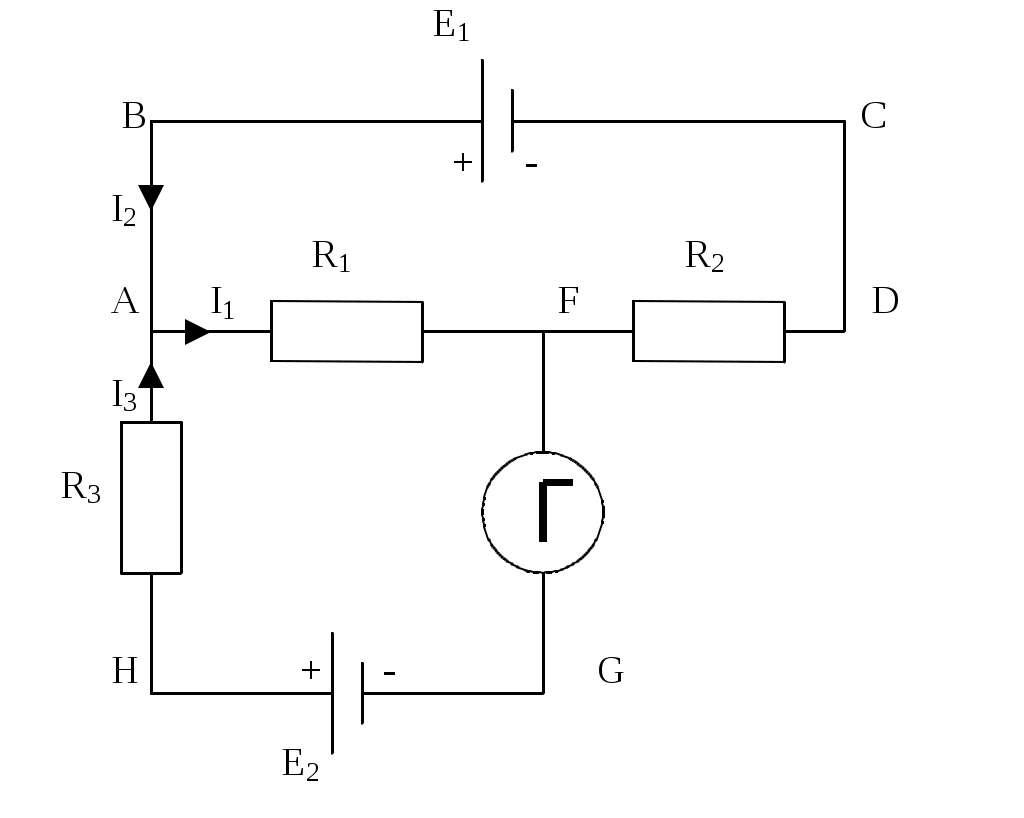
Индукция в точке B определяется только зарядами, находящимися на внутреннем цилиндре. Ее можно найти по формуле:

, (1)

где τ₁ – линейная плотность заряда внутреннего цилиндра:

. Отсюда



Подставляя численные данные, получим E₂ = 4,7 10²В/м.

Для точки С находим индукцию D₃ по принципу суперпозиции:

D₃ = D₁(r₃)-D₂(r₃), (2)

где D₁(r₃) – индукция поля, создаваемого внутренним цилиндром, D₂(r₃) – индукция поля, создаваемого внешним цилиндром в точке С. Находя D₁ и D₂, аналогично (1), и подставляя в (2) получим

,

отсюда .

Подставляя численные данные, получим Е₃= 1,5 10² В/м.
Пример 5. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра (рис.4).

Рис.4

Вэтой цепи r₁= 100 Ом, r₂₌50 Ом, r₃=20 Ом, Э.Д.С. элемента E₁=2 В Гальванометр регулирует ток I₃=50 мА, идущий в направлении, указанном стрелкой. Определить Э.Д.С. E₂ второго элемента. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
Решение. Применим правила Кирхгофа. Выберем направления токов, как они показаны на рис.4, и условимся обходить контуры по часовой стрелке.

По первому правилу Кирхгофа для узла F имеем

I₁-I₂-I₃=0

По второму правилу Кирхгофа имеем для контура ABCDFA

-I₁r₁-I₂r₂=-E₁ ,

или после умножения обеих частей равенства на -1.

I₁r_{1 +} I₂r₂=E₁

Соответственно, для контура AFGHA

I₁r₁+I₃r₃=E₂

После подстановки числовых значений в формулы получим: I₁-I₂-0,05=0;

50I₁+25I₂=1;

100I₁+0,05·20=E₂

Перенеся в этих уравнениях неизвестные величины в левые части, а известные - в правые, получим следующую систему урав­нений:

I₁-I₂=0,05

50I₁+25I₂=1

100I₁-E₂= -1

Эту систему с тремя неизвестными можно решить обычными приемами алгебры, но так как по условию задачи требуется опре­делить только одно неизвестное E₂их трех, то воспользуемся методом определителей.

Составим и вычислим определитель системы: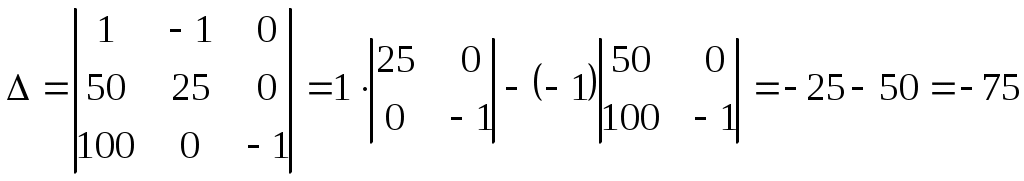

Составим и вычислим определитель ΔE₂:

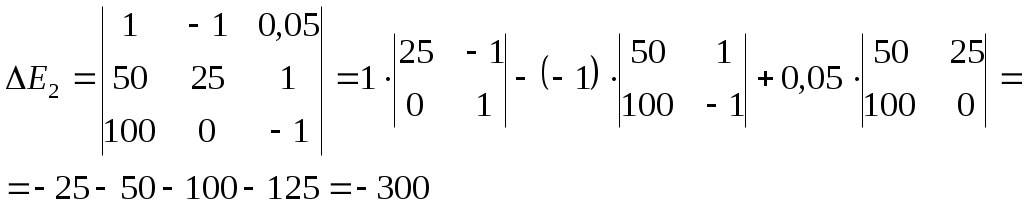Разделив определитель ΔE₂ на определитель Δ, найдем числовое значение Э.Д.С. E₂: E₂= -300 -75=4В.

Заряды.Закон Кулона.

1. 
   Какой заряд приобрел бы медный шар с радиусом 10 см, если бы удалось удалить все электроны проводимости? Плотность меди 8,9 г/см³, относительная атомная масса равна 64. Заряд электрона 1,6 10^-19 Кл, число Авогадро 6·10²³ моль^-1. Считать, что на каждый атом меди приходится один электрон проводимости.
   
2. 
   С какой силой будут притягиваться два одинаковых свинцовых шарика радиусом 1 см, расположенные на расстоянии 1 м друг от друга, если у каждого атома первого шарика отнять по одному электрону и все эти электроны перенести на второй шарик? Относительная атомная масса свинца А=207, плотность 11,3 г/см³.
   
3. 
   На двух одинаковых капельках воды находятся по одному лиш­нему электрону, причем сила электрического отталкивания капелек уравновешивает силу их взаимного тяготения. Каковы радиусы капелек?
   
4. 
   Три точечных заряда, расположенные на расстоянии 10 см друг от друга, взаимодействуют друг с другом с силами 5 Н, 8 Н, 12 Н, соответственно. Найти величину каждого из зарядов.
   
5. 
   Найти силу взаимодействия двух точечных зарядов 2 10^-7 Кл и 3 10^-7 Кл в вакууме и в керосине на расстоянии 20 см, если диэлектрическая проницаемость керосина равна 2.
   
6. 
   Два маленьких шарика обладают зарядами 2·10^-7 Кл и 4,5·10^-7 Кл и, находясь в вакууме, взаимодействуют с силой 0,1 Н. Вычислить расстояние между шариками.
   
7. 
   Два шарика, массой 1 г каждый, подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол 60°?
   
8. 
   Три точечных заряда 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
   
9. 
   Вокруг неподвижного точечного заряда +10^-9 Кл равномерно вращается под действием электростатической силы притяжения маленький шарик, заряженный отрицательно. Чему равно отношение заряда шарика к его массе, если радиус орбиты 2см, а, угловая скорость вращения 3 рад/с?
   
10. 
    Два маленьких одинаковых проводящих шарика, с зарядами q₁=-3,5·10^-9 и q₂=2,5·10^-9 Кл соединили а затем поместили нарасстоянии 5 см друг от друга. Определить заряды каждого из шариков и силу электрического взаимодействия между ними после соприкосновения.
    
11. 
    Шарик массой 2 г, имеющий заряд 2·20^-7 Кл, подвешен в воздухе на тонкой изолированной нити. Определить натяжение нити, если снизу на расстоянии 15 см расположен такой же заряд.
    
12. 
    Электрические заряды двух туч соответственно равны 20 Кл и 30 Кл. Среднее расстояние между тучами 30 км. С какой силой взаимодействуют тучи?
    
13. 
    С какой силой отталкиваются два электрона, находящиеся друг от друга на расстоянии 2·10^-8 см?
    
14. 
    Три одинаковых точечных тела с зарядами по 2 нКл находятся в вершинах равностороннего треугольника со сторонами 10 см. Определить модуль и направление силы, действующей на один из зарядов со стороны двух других.
    
15. 
    Два положительных точечных заряда Q и 9Qзакреплены на расстоянии 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
    
16. 
    Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на определенный угол. Шарики погружают в масло. Какова плотность масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков 1,5 г/см³, диэлектрическая проницаемость масла 2,2.
    
17. 
    Четыре одинаковых точечных тела с зарядами по 40 нКл каждое, закреплены в вершинах квадрата со стороной 10 см. Найти силу, действующую на одно из этих тел со стороны трех остальных.
    
18. 
    Каждый из двух шариков массой по 1г несет электрический заряд 10^-9 Кл. Во сколько раз сила электрического взаимодействия больше силы гравитационного притяжения?
    
19. 
    Два точечных заряда находятся на некотором расстоянии друг от друга. Если расстояние между ними уменьшается на 50 см, то сила взаимодействия увеличивается в два раза. Найти это расстояние.
    
20. 
    Отрицательный заряд расположен на прямой, соединяющей два одинаковых положительных точечных заряда. Расстояние между отрицательным зарядом и каждым из положительных относятся между собой как 1:3. Во сколько paз изменится сила, действующая на отрицательный заряд, если его поменять местами с ближайшим положительным.
    

Электрическое поле. Напряженность электрического поля.

21. 
    По тонкой нити, изогнутой по дуге окружности радиусом 10 см, равномерно распределен заряд 20 нКл. Определить напряженность поля, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины дуги окружности.
    
22. 
    Определить напряженность поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню с линейной плотностью заряда 200нКл/м, в точке, лежащей на продолжении оси стержня на расстоянии 20 см от ближайшего конца. Длина стержня 40 см.
    
23. 
    На продолжении оси тонкого прямого стержня, равномерно заряженного с линейной плотностью заряда 15 нКл/см, на расстоянии 40 см от конца стержня находится точечный заряд 10нКл. Второй конец стержня уходит в бесконечность. Определить силу взаимодействия стержня и заряда.
    
24. 
    По тонкому кольцу радиусом 10 см равномерно распределен заряд 20 нКл. Какова напряженность E поля в точке, находящейся на оси кольца на расстоянии 20 см от центра кольца?
    
25. 
    Два длинных тонких равномерно заряженных стержня с линейной плотностью заряда 1 мкКл/м расположены в одной плоскости перпендикулярно друг другу так, что точка пересечения их осей находится на расстоянии 10 см и 15 см от ближайших концов стержней. Найти силу, действующую на заряд 10 нКл, помещенный в точку пересечения осей стержней.
    
26. 
    Две длинные прямые параллельные нити находятся на расстоянии 5 см друг от друга. На нитях равномерно распределены заряды с линейной плотностью – 5нКл/см и 10 нКл/см. Определить напряженность Е электрического поля в точке, удаленной от первой нити на расстояние 3 см и от второй - на расстояние 4 см.
    
27. 
    Электрон с начальной скоростью υ₀ =3 Мм/с влетел в однородное электрическое поле напряженностью Е=150В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Определить: 1)силу, действующую на электрон; 2)ускорение электрона; 3) скорость электрона через t=0,1мкс.
    
28. 
    Напряженность поля между горизонтально расположенными обкладками плоского кон­денсатора равна 6000 В/м. Определить массу помещенной в это поле пылинки, если она несет заряд 1,6·10^-11Кл и находится в рав­новесии.
    
29. 
    С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости с одинаковой поверхностной плотностью заряда равной 2 мкКл/м²?
    
30. 
    К бесконечной равномерно заряженной вертикальной плоскости подвешен на нити одноименно заряженный шарик массой 50 мг и зарядом 0,6 нКл. Сила натяжения нити, на которой висит шарик 0,7мН. Найти поверхностную плотность заряда плоскости.
    
31. 
    Тонкое полукольцо радиусом 20 см несет равномерно распределенный заряд 2 мкКл. Определить силу, действующую на точечный заряд 40 мкКл, расположенный в центре кривизны полукольца.
    
32. 
    Определить напряженность E поля, создаваемого тонким длинным стержнем, равномерно заряженным с линейной плотностью заряда 20 мкКл/м в точке, находящейся на расстоянии 2 см от стержня, вблизи его середины.
    
33. 
    Параллельно бесконечной плоскости, заряженной с поверхностной плотностью заряда 4 мкКл/м², расположена бесконечно длинная прямая нить, заряженная с линейной плотностью заряда 100 нКл/м. Определить силу, действующую со стороны плоскости на отрезок нити длиной 1 м.
    
34. 
    Две одинаковые круглые заряженные пластины, площадью 400 см² каждая, расположены параллельно друг другу. Заряд одной пластины 400 нКл, другой -200 нКл. Определить силу взаимного притяжения пластин, если расстояние между ними: а) 3 мм; б) 10 м.
    
35. 
    С какой силой (на единицу длины) взаимодействуют две заряженные бесконечно длинные параллельные нити с одинаковой линейной плотностью заряда 20 мкКл/м, находящиеся на расстоянии 10 см друг от друга?
    
36. 
    Поверхностная плотность заряда бесконечно протяженной вертикальной плоскости равна 400 мкКл/м². К плоскости на нити подвешен одноименно заряженный шарик массой 10 г. Определить заряд шарика, если нить образует с плоскостью угол 30^о.
    
37. 
    На бесконечном тонкостенном цилиндре диаметром 20 см равномерно распределен заряд с поверхностной плотностью 4 мкКл/м². Определить напряженность поля в точке, отстоящей от поверхности цилиндра на 15 см.
    
38. 
    Тонкий длинный стержень равномерно заряжен с линейной плотностью 1,5 нКл/м. На продолжении оси стержня на расстоянии 12 см от его конца находится точечный заряд 0,2 мкКл. Определить силу взаимодействия стержня и точечного заряда. Длина стержня 24 см.
    
39. 
    Длинная прямая тонкая проволока несет равномерно распределенный заряд. Вычислить линейную плотность заряда, если напряженность поля на расстоянии 0,5 м от проволоки против ее середины 2 В/см.
    
40. 
    По тонкому кольцу равномерно распределен заряд 10 нКл с линейной плотностью 0,01 мкКл/м. Определить напряженность электрического поля, создаваемого заряженным кольцом в точке, лежащей на оси кольца и удаленной от его центра на расстояние, равное радиусу кольца.
    
41. 
    Две трети тонкого кольца радиусом 10 см несут равномерно распределенный заряд с линейной плотностью 0,2 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
    
42. 
    Тонкий бесконечный стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью 0,5 мкКл/м. Определить напряженность электрического поля, создаваемого этим зарядом в точке, лежащей на оси стержня на расстоянии 20 см от его начала.
    
43. 
    По тонкому кольцу радиусом 20 см равномерно распределен заряд с линейной плотностью 0,2 мкКл/м. Определить напряженность электрического поля, создаваемого заряженным кольцом в точке, находящейся на оси кольца на расстоянии от центра, равном удвоенному радиусу кольца.
    
44. 
    По тонкому полукольцу равномерно распределен заряд 20 нКл с линейной плотностью 0,1 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
    
45. 
    Четверть тонкого кольца радиусом 10 см несет равномерно распределенный заряд 0,05 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
    
46. 
    Тонкий стержень длиной 20 см несет равномерно распределенный заряд 0,1 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, лежащей на оси стержня на расстоянии 20 см от его конца.
    
47. 
    По тонкому кольцу радиусом 10 см равномерно распределен заряд с линейной плотностью 1 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
    
48. 
    Тонкое кольцо несет распределенный заряд 0,2 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, равноудаленной от всех точек кольца на расстояние 20 см. Радиус кольца 10 см.
    
49. 
    Треть тонкого кольца радиусом 10 см несет распределенный заряд 50 нКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
    
50. 
    Определить напряженность поля в точке, лежащей между зарядами +2·10^-7 Кл и -4·10^-7 Кл, находящимися в скипидаре на расстоянии 10 см друг от друга.
    
51. 
    На каком расстоянии от точечного заряда 1·10^-7 Кл, находящегося в дистиллированной воде (ε=81), напряженность электрического поля будет равна 0,25 В/м.
    
52. 
    Одинаковые по величине, но разные по знаку заряды 1,8·10^-8 Кл расположены в двух вершинах равностороннего треугольника. Сторона треугольника 2 м. Определить напряженность электрического поля в третьей вершине треугольника.
    
53. 
    В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены положительные заряды q. В вершине при одном из тупых углов ромба помещен положительный заряд Q. Определить напряженность электрического поля Е в четвертой вершине ромба.
    

Потенциал электрического поля. Связь напряженности и потенциала.

54. 
    Точечные заряды 4·10^-7 Кл и 5·10^-7 Кл находятся на расстоянии 0,5 м друг от друга. Какую работу необходимо совершить, чтобы сблизить эти заряды до расстояния 0,2 м?
    
55. 
    Пылинка массой 10^-4 г находится в электрическом поле между горизонтальными заряженными пластинами. Разность потенциалов между пластинами равна 10 кВ, расстояние между ними 5 см. Каким электрическим зарядом обладает пылинка, если она находится в равновесии?
    
56. 
    Электрическое поле создано длинным цилиндром, равномерно заряженным с линейной плотностью 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся вне цилиндра на расстоянии 0,5 см и 2 см от его поверхности, если радиус цилиндра - 1 см.
    
57. 
    Заряд равномерно распределен по бесконечной плоскости с поверхностной плотностью 10 мкКл/м². Определить разность потенциалов двух точек этого поля, если одна из точек находится на плоскости, а другая удалена от нее на расстояние 10 см.
    
58. 
    По тонкому кольцу радиусом 10 см равномерно распределен заряд с линейной плотностью 10 нКл/м. Определить потенциал в точке, лежащей на оси кольца на расстоянии 5 см от центра.
    
59. 
    На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью 10 нКл/м. Вычислить потенциал поля, создаваемого этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
    
60. 
    Тонкий стержень длиной 10 см несет равномерно распределенный заряд 1нКл. Определить потенциал электрического поля в точке, лежащей на оси стержня на расстоянии 20 см от ближайшего его конца.
    
61. 
    Тонкий стержень изогнут в форме квадрата. Стержень заряжен с линейной плотностью 1,6 нКл/м. Найти потенциал электрического поля в центре квадрата.
    
62. 
    Бесконечно длинная тонкая прямая нить несет равномерно распределенный по длине нити заряд с линейной плотностью 0,01мкКл/м. Определить разность потенциалов двух точек поля, удаленных от нити на 2 см и 4 см.
    
63. 
    Определить потенциальную энергию электростатического взаимодействия двух точечных зарядов 400нКл и 20 нКл, находящихся на расстоянии 5 см друг от друга.
    
64. 
    Две параллельные заряженные плоскости, поверхностные плотности зарядов которых 2 мкКл/м² и 0,8 мкКл/м², находятся на расстоянии 0,6 см друг от друга. Определить разность потенциалов между плоскостями.
    
65. 
    Какая работа совершается электрическим полем при перемещении заряда 4,6 мкКл в поле между точками с разностью потенциалов 2000 В?
    
66. 
    Определить потенциал на поверхности шара, если известно, что на расстоянии 10 см от его поверхности потенциал электрического поля равен 20 В. Радиус шара 0,1 м.
    
67. 
    Заряженная капелька масла уравновешена электростатическим полем горизонтально расположенного плоского конденсатора, находящегося под напряжением 250 В. Чему равна масса капельки, если она несет на себе заряд равный заряду трех электронов? Расстояние между пластинами 8мм.
    
68. 
    Капелька масла радиусом 1 мкм, несущая на себе заряд двух электронов, находится в равновесии в поле расположенного горизонтально плоского конденсатора, когда к нему приложено напряжение 820 В. Расстояние между пластинами 8 мм. Плотность масла 0,8 г/см³. Чему равен заряд электрона?
    
69. 
    Два одинаково равномерно заряженных шарика, расположенных друг от друга на расстоянии 25 см (между центрами), взаимодействуют с силой 1·10^-6Н. До какого потенциала заряжены шарики, если их диаметр 1 см?
    
70. 
    Металлический шар радиуса 5 м, заряженный до потенциала 100 В, окружают сферической проводящей оболочкой ра­диуса 10 м. Как изменится потенциал шара, после того как он будет на некоторое время соединен проводником с оболочкой?