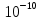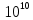ФОМНЭ_ИДЗ2. Основные положения квантовой механики
 Скачать 39.27 Kb. Скачать 39.27 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Микрорадиоэлектроники и технологии радиоаппаратуры (МИТ) отчет по “Физические основы микро и нано-электроники” практике Тема: «Основные положения квантовой механики»
Санкт-Петербург 2021 ЗАДАНИЕ на “Физические основы микро и нано-электроники” практику
«Волновой дуализм де Бройля» 1.1. Теоретический материал Рассчитать длину волны де Бройля для частицы массой m, движущейся со скоростью v, используя формулу 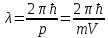 где длина волны, которую можно сопоставить с частицей; волновой вектор k направлен по движению частицы; ħ квант действия, равный отношению постоянной Планка h к 2 (1,051027 эргсек). 1.2. Решение задачи   «Принцип неопределенности Гейзенберга» 2.1. Теоретический материал Определить ошибку в определении физической величины, налагаемой соотношением неопределенности Гейзенберга, используя формулу 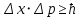 При выполнении заданий особое внимание обратить на правильность применения размерности величин. 2.2. Решение задачи 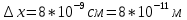   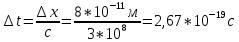 Вывод: Была рассчитана волна де Бройля для заданных параметров 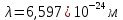 . Можно сказать, что чем больше импульс частицы, тем меньше длина волны де Броля, в данном случае длина волны слишком мала для из обнаружения. . Можно сказать, что чем больше импульс частицы, тем меньше длина волны де Броля, в данном случае длина волны слишком мала для из обнаружения.Была рассчитана неопределенность в энергии частицы в соответствии соотношением неопределенности Гейзенберга  , при , при  . .Данные полученные во втором задании можно трактовать 3 способами:  – неопределенность энергии состояния микрообъекта, пребывающего в этом состоянии время – неопределенность энергии состояния микрообъекта, пребывающего в этом состоянии время 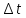 . . - неопределенность энергии микрообъекта в некотором процессе длительностью - неопределенность энергии микрообъекта в некотором процессе длительностью 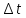 . . – максимальная точность определения энергии квантовой системы, достижимая путем процесса измерения, длящегося время – максимальная точность определения энергии квантовой системы, достижимая путем процесса измерения, длящегося время 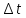 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||