Исследование разомкнутой линейной системы. Теория автоматизированного управления.. Исследование разомкнутой линейной системы. Отчет по лабораторной работе 1 Исследование разомкнутой линейной системы Проверил Уфа 2021
 Скачать 435.14 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» ОТЧЕТ по лабораторной работе № 1 Исследование разомкнутой линейной системы Выполнил: Проверил: Уфа 2021 Цель работы: - освоение методов анализа одномерной линейной непрерывной системы с помощью среды SCILAB. Задачи работы: - ввести модель системы в виде передаточной функции; - построить эквивалентные модели в пространстве состояний и в форме «нули - полюса»; - определить коэффициент усиления в установившемся режиме и полосу пропускания системы; - научиться строить импульсную и переходную характеристики, карту расположения нулей и полюсов, частотную характеристику. Теоретическая часть Работу любой системы регулирования можно описать словесно. Словесное описание помогает понять принцип действия системы, ее назначение, особенности функционирования и т.д. Однако, что самое главное, оно не дает количественных оценок качества регулирования, поэтому не пригодно для изучения характеристик систем и построения систем автоматизированного управления. Вместо него в теории автоматизированного управления используются более точные математические методы описания свойств систем: - статические характеристики, - временные характеристики, - дифференциальные уравнения, - передаточные функции, - частотные характеристики и др. 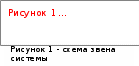 В любой из этих моделей система может быть представлена в виде звена, имеющего входные воздействия Х, возмущения F и выходные воздействия Y (см. рисунок 1). Под влиянием входных воздействий выходная величина может изменяться. После того, как получено математическое описание системы, можно перейти к одной из задач, ради которых, собственно, и получалось это математическое описание – к задаче анализа. Первой и главной задачей анализа является определение устойчивости системы. Этот вопрос важен, потому, что в большинстве случаев неустойчивая система непригодна для практического использования, и, потому, что даже в устойчивых системах нужно знать, какие запасы устойчивости она (система) имеет. В результате анализа устойчивости обычно недостаточно получить прямой и однозначный ответ на вопрос, устойчива ли система. В большинстве практических случаев инженеру-проектировщику необходимо ясно представлять себе, какие из параметров элементов системы наиболее сильно влияют на устойчивость, и как их следует изменить, чтобы обеспечить необходимый запас устойчивости. Для описания линейных систем могут применяться несколько способов: ● дифференциальные уравнения ● модели в пространстве состояний ● передаточные функции ● модели вида «нули-полюса» Первые два способа называются временными, поскольку описывают поведение системы во временной области и отражают внутренние связи между сигналами. Передаточные функции и модели вида «нули-полюса» относятся к частотным способам описания, так как непосредственно связаны с частотными характеристиками системы и отражают только вход-выходные свойства (то есть, описывают динамику не полностью). Частотные методы позволяют применять для анализа и синтеза алгебраические методы, что часто упрощает расчеты. С другой стороны, для автоматических вычислений более пригодны методы, основанные на моделях в пространстве состояний, поскольку они используют вычислительно устойчивые алгоритмы линейной алгебры. Исходные уравнения динамики объектов, которые строятся на основе законов физики, имеют вид нелинейных дифференциальных уравнений (ДУ). Для приближенного анализа и синтеза обычно проводят их линеаризацию в окрестности установившегося режима и получают линейные дифференциальные уравнения. Исследование автоматической системы регулирования (АСР) существенно упрощается при использовании прикладных математических методов операционного исчисления, поскольку позволяет от решения дифференциальных уравнений перейти к решению алгебраических уравнений. Например, функционирование некоторой системы описывается ДУ вида 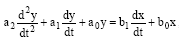 ,где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что  , (1)то исходное уравнение при нулевых начальных условиях равносильно линейному алгебраическому уравнению:  (2)Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением. Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s). Переход от одной модели к другой достаточно прост и заключается в замене знаков дифференциалов  на операторы sn, знаков интегралов  на множители  , а самих x(t) и y(t) - изображениями X(s) и Y(s).Преобразование ДУ по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы. Например, операторное уравнение 3s2Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s) можно преобразовать, вынеся X(s) и Y(s) за скобки и поделив друг на друга: Y(s)*(3s2 + 4s + 1) = X(s)*(2s + 4) 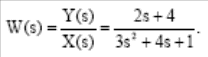 Полученное выражение называется передаточной функцией. Передаточной функцией называется отношение изображения выходного воздействия Y(s) к изображению входного X(s) при нулевых начальных условиях.  (3)Передаточная функция является дробно-рациональной функцией комплексной переменной: 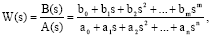 где B(s) = b0 + b1s + b2s2 + … + bmsm - полином числителя, А(s) = a0 + a1s + a2s2 + … + ansn - полином знаменателя. Передаточная функция имеет порядок, который определяется порядком полинома знаменателя (n). Из (3) следует, что изображение выходного сигнала можно найти как Y(s) = W(s)*X(s). Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета АСР сводится к определению ее передаточной функции. Одна из важнейших характеристик линейной системы – коэффициент усиления в установившемся режиме или статический коэффициент усилении (static gain, DC-gain). Его можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице. Размерность этой величины равна отношению размерностей сигналов выхода и выхода. Если задана передаточная функции, для вычисления ks надо подставить в нее s=0, поскольку переменная соответствует оператору дифференцирования. Если система содержит интегрирующее звено (передаточная функция имеет полюс в точке s=0), этот предел равен бесконечности, то есть, при постоянном сигнале выход бесконечно увеличивается или уменьшается, не достигая установившегося режима. Импульсной характеристикой (весовой функцией) w(t) называется реакция системы на единичный бесконечный импульс (дельта-функцию или функцию Дирака) при нулевых начальных условиях. Дельта-функция (t) определяется равенствами: 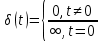 ,  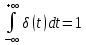Это обобщенная функция – математический объект, представляющий собой идеальный сигнал, никакое реальное устройство не способно его воспроизвести. Дельта - функцию можно рассматривать как предел прямоугольного импульса единичной площади с центром в точке при стремлении ширины импульса к нулю. Импульсная характеристика отражает лишь вход-выходные соотношения при нулевых начальных условиях, то есть, не может полностью описывать динамику системы. Переходной характеристикой (переходной функцией) h(t) называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок): 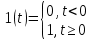 Импульсная и переходная функции связаны выражениями: 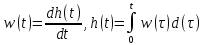 Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке s=0) стремится к нулю. Если система содержит интегрирующие звенья, переходная характеристика асимптотически стремится к прямой, параболе и т.д., в зависимости от количества интеграторов. По определению предельное значение переходной функции h(t) при t есть статический коэффициент усиления: 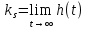 Эта величина имеет смысл только для устойчивых систем, поскольку при неустойчивости переходный процесс не сходится к конечному значению. По переходной характеристике можно найти важнейшие показатели качества системы - перерегулирование (overshoot) и время переходного процесса (settling time).  Перерегулирование определяется как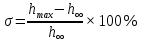 ,где hmax - максимальное значение функции h(t), а 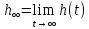 - установившееся значение выхода (рис 2).Если установившееся значение отрицательное, при вычислении перерегулирования нужно выполнить «зеркальное отражение» сигналов - поменять знаки у h(t) и hmax. В формуле вместо максимального значения нужно взять минимальное: 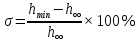 Время переходного процесса – это время, после которого сигнал выхода отличается от установившегося значения не более чем на заданную малую величину (обычно 2% или 5% от установившегося значения). При подаче на вход линейной системы гармонического (синусоидального) сигнала  с частотой  (она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы  , где  – амплитуда и  – сдвиг фазы.Частотная характеристика определяется как реакция системы на комплексный экспоненциальный сигнал  . Для ее построения надо использовать подстановку  в передаточной функции  . Выражение  называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).Зависимость модуля величины от частоты называется амплитудной частотной характеристикой (АЧХ), а зависимость аргумента комплексного числа (фазы) от частоты – фазовой частотной характеристикой (ФЧХ): .АЧХ показывает, насколько усиливается амплитуда сигналов разных частот после прохождения через систему, а ФЧХ характеризует сдвиг фазы сигнала. Реальные объекты имеют строго правильную передаточную функцию, поэтому их АЧХ убывает с ростом частоты и асимптотически стремится к нулю. Говорят, что такой объект обладает свойством фильтра - фильтрует (не пропускает) высокочастотные сигналы (помехи, шумы измерений). Это свойство служит основой для использования метода гармонического баланса. Максимум АЧХ соответствует частоте, на которой усиление наибольшее. Значение АЧХ при  равно усилению при постоянном сигнале, то есть, статическому коэффициенту усиления  . Это следует и из равенства .Для систем с интегрирующими звеньями частотная характеристика стремится к бесконечности при  . Это значит, что их выход бесконечно увеличивается или уменьшается при постоянном входном сигнале.Практическая часть 1. Описание системы Исследуется система, описываемая математической моделью в виде передаточной функции: 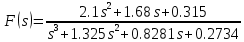 2. Результаты исследования нули передаточной функции: -0.5 + 0.i, -0.3 + 0.i полюса передаточной функции: -0.700 + 0.i, -0.313 + 0.541i, -0.313 - 0.541i коэффициент усиления звена в установившемся режиме: k=1.152 модель системы в пространстве состояний: 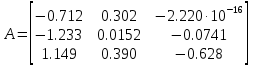 , ,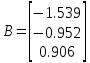 ,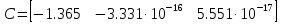D=0 статический коэффициент усиления после изменения матрицы D: k1= 2.152 Cвязь между k и k1 объясняется тем, что при нахождении статического коэффициента передачи через модель в пространстве состояний используется формула ks=-CA-1B+D, в которой есть слагаемое D. В случае системы с одним входом и одним выходом это просто скалярная величина, значение которой изменилось с нуля на единицу, поэтому k1 больше k ровно на 1. Разница между who и whos заключается в том, что команда who выводит только названия используемых в данный момент переменных, а команда whos кроме названия переменных выводит их тип и занимаемый в памяти размер в байтах.  Переменные %e и %pi являются системными переменными (в данном случае константами) и соответственно равны числу e=2.72 и числу =3.14. Системные переменные нельзя переопределить, например, переменным %e и %pi нельзя присвоить другие значения. Расположение нулей и полюсов (рис. 3): коэффициенты демпфирования и частоты среза:
 Импульсные характеристики исходной и модифицированной систем (рис. 4): Импульсные характеристики систем f и f_ss получились одинаковые, т.к. для модели f_ss () импульсная характеристика построена неправильно. В момент времени t=0 она должна быть бесконечной по величине, и система Scilab в таком случае строит импульсную характеристику для строго правильной части, принимая D=0, т. е. для модели f.  Переходные процессы исходной и модифицированной систем (рис. 5): Различие между переходными характеристиками состоит в том, что выход системы f_ss стабилизируется на более высоком уровне чем система f, и объясняется тем, что система f_ss имеет увеличенный на единицу статический коэффициент усиления. Характеристики переходного процесса:
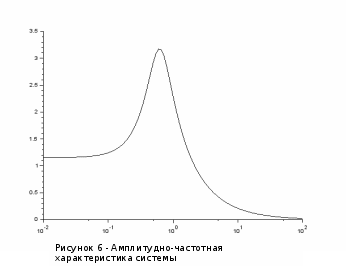 Амплитудная частотная характеристика замкнутой системы (рис. 6):         B wc ks Показатель колебательности системы: М= 2.753 статический коэффициент усиления ks=1.152 На АЧХ его можно найти по значению величины горизонтального участка графика работы системы (см. рис 6). Частота среза: wc=2.154 рад/с По АЧХ частоту среза можно найти, проведя горизонтальную линию при коэффициенте усиления равном единице и проецируя положение точки пересечения с графиком на ось абсцисс (см. рис 6). Полоса пропускания: B=2.420 рад/c По АЧХ полосу пропускания можно найти, проведя горизонтальную линию от величины коэффициента усиления, умноженного на 0.707 и проецируя положение точки пересечения с графиком на ось абсцисс (см. рис. 6) |