Отчет по лабораторной работе 134 Измерение коэффициента теплопроводности воздуха
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
|
Нижегородский государственный университет им. Н. И. Лобачевского Отчет по лабораторной работе № 134 «Измерение коэффициента теплопроводности воздуха» Дата протокола 11.02.20 Дата отчета 03.03.20 Выполнила: Студентка 1 курса ВШ ОПФ Петрова Ирина Проврил:к.ф.-м.н. Викторов Михаил Евгеньевич Цель работы – изучение теплопроводности воздуха как одного из явлений переноса в газах, измерение коэффициента теплопроводности воздуха, сравнение полученных результатов с табличными Оборудование: экспериментальная установка ФПТ-3 Теоретическая часть Теплопередача в газах осуществляется тремя способами: тепловым излучением, конвекцией и теплопроводностью. При теплопроводности осуществляется непосредственная передача энергии от молекул с большей энергией к молекулам с меньшей энергией. Для стационарного процесса, при котором разность температур в слое газа не изменяется со временем, количество теплоты dQ, которое переносится за время dt через площадку S, перпендикулярно к направлению r переноса энергии определяется по закону Фурье:  , (1) , (1)где k – коэффициент теплопроводности;  – градиент температуры. Для идеального газа – градиент температуры. Для идеального газа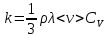 (2) (2)где  - плотность газа; 𝜆 – средняя длина свободного пробега; - плотность газа; 𝜆 – средняя длина свободного пробега;  - средняя скорость теплового движения молекул, равная - средняя скорость теплового движения молекул, равная  , ,  - удельная теплоёмкость газа при постоянном объёме. - удельная теплоёмкость газа при постоянном объёме.Рассмотрим два коаксиальных цилиндра, пространство между которыми заполнено газом. Если внутренний цилиндр нагревать, а температуру наружного цилиндра поддерживать постоянной (ниже температуры нагревателя), то в кольцевом слое газа возникает тепловой поток, направленный от внутреннего цилиндра к наружному. При этом температура слоёв газа, прилегающих к стенкам цилиндров, равна температуре стенок. Выделим в газе кольцевой слой радиусом r, толщиной dr и длиной L. По закону Фурье (1)  количество теплоты, которое проходит через этот слой за одну секунду, можно записать в виде количество теплоты, которое проходит через этот слой за одну секунду, можно записать в виде . (3) . (3)Разделяя переменные, получим 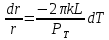 . .Считая, что диаметр и температура внутреннего цилиндра равны соответственно d и  , а внешнего D и , а внешнего D и  , проинтегрируем дифференциальное уравнение: , проинтегрируем дифференциальное уравнение: то есть  . (4) . (4)Из уравнения (4) получим формулу для определения коэффициента теплопроводности газа 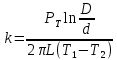 (5) (5)Формула (5) получена в предположении, что теплота переносится от внутреннего цилиндра к наружному только благодаря теплопроводности ( а оно достаточно обосновано, поскольку поток энергии при невысоких температурах и малом диаметре нагревателя составляет незначительную часть переносимого количества теплоты, а конвекция устраняется подбором диаметра наружного цилиндра и его вертикальным расположением в экспериментальной установке). Внутренним цилиндром в работе служит вольфрамовая проволока, которая нагревается электрическим током. После установления стационарного режима мощность тепловых потерь можно принять равной тепловой мощности, выделяющейся при протекании по проволоке электрического тока  , ,где  – ток через проволоку, – ток через проволоку,  - падение напряжения на проволоке. - падение напряжения на проволоке.Если последовательно с проволокой включить эталонный резистор 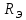 , то , то  , ,и тогда  , (6) , (6)где  - падение напряжения на эталонном резисторе. Используя равенство (6) в формуле (5), получим - падение напряжения на эталонном резисторе. Используя равенство (6) в формуле (5), получим . .Здесь Dи d – диаметры наружного цилиндра и проволоки;  – разность температур проволоки и наружного цилиндра (трубки). Температуру трубки – разность температур проволоки и наружного цилиндра (трубки). Температуру трубки  можно принять равной температуре окружающего воздуха. можно принять равной температуре окружающего воздуха.Для вычисления разности температур  в слое газа напишем формулы, по которым определяют сопротивление проволоки при температуре окружающего воздуха и в нагретом состоянии: в слое газа напишем формулы, по которым определяют сопротивление проволоки при температуре окружающего воздуха и в нагретом состоянии: где α – температурный коэффициент сопротивления материала проволоки, а 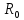 – сопротивление проволоки при – сопротивление проволоки при  . Исключив из этих равенств . Исключив из этих равенств 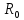 , найдём , найдём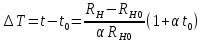 Учитывая, что  получаем получаем Здесь  , , 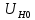 - падение напряжения на проволоке соответственно в нагретом состоянии и при температуре - падение напряжения на проволоке соответственно в нагретом состоянии и при температуре 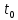 окружающего воздуха; окружающего воздуха;  - падение напряжения на эталонном резисторе соответственно при нагретой проволоке и при температуре окружающего воздуха - падение напряжения на эталонном резисторе соответственно при нагретой проволоке и при температуре окружающего воздуха 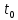 . . Экспериментальная установка Экспериментальная установкаОбщий вид экспериментальной установки (см.рис.1): 1 – блок приборов; 2 – цифровой термометр; 3 – блок рабочего элемента; 4 – вольфрамовая проволока; 5 – цифровой вольтметр; 6 – датчик температуры.  Рис.1 Рабочий элемент установки представляет собой стеклянную трубку, заполненную воздухом, вдоль оси которой натянута вольфрамовая проволока 4. Температура трубки в ходе эксперимента поддерживается постоянной благодаря принудительной циркуляции воздуха между трубкой и кожухом блока рабочего элемента 3, которая осуществляется с помощью вентилятора, находящегося в блоке рабочего элемента. Температура воздуха в кожухе (а, следовательно, и температура самой трубки) измеряется цифровым термометром 2. Падение напряжения на эталонном резисторе  и на проволоке и на проволоке  измеряется цифровым вольтметром. Величина напряжения на проволоке регулируется ручкой «Нагрев», которая выведена на переднюю панель блока приборов 1. Диаметр трубки D, диаметр проволоки d, длина трубки L и температурный коэффициент сопротивления материала проволоки α указаны на рабочем месте: измеряется цифровым вольтметром. Величина напряжения на проволоке регулируется ручкой «Нагрев», которая выведена на переднюю панель блока приборов 1. Диаметр трубки D, диаметр проволоки d, длина трубки L и температурный коэффициент сопротивления материала проволоки α указаны на рабочем месте:  . .Экспериментальная часть Включив установку тумблером «Сеть», и включив тумблер «Нагрев», начнём увеличивать напряжение на проволоке. Нажав кнопку «  » (режим измерения падения напряжения на эталонном резисторе) и с помощью регулятора «Нагрев» установим падение напряжения на эталонном резисторе » (режим измерения падения напряжения на эталонном резисторе) и с помощью регулятора «Нагрев» установим падение напряжения на эталонном резисторе  не более 1,2В. При этом температура проволоки остаётся практически неизменной. Затем при том же положении регулятора «Нагрев» нажмём кнопку « не более 1,2В. При этом температура проволоки остаётся практически неизменной. Затем при том же положении регулятора «Нагрев» нажмём кнопку « » (режим измерения падения напряжения на проволоке) и зарегистрируем значение напряжения » (режим измерения падения напряжения на проволоке) и зарегистрируем значение напряжения 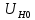 . Опыт проведём пять раз для пяти близких значений к . Опыт проведём пять раз для пяти близких значений к  , не превосходящем 1,2В. Результаты занесём в таблицу 1: , не превосходящем 1,2В. Результаты занесём в таблицу 1:
Далее продолжим эксперимент. Нажмём кнопку «  » и с помощью регулятора «Нагрев» установим падение напряжения на эталонном резисторе » и с помощью регулятора «Нагрев» установим падение напряжения на эталонном резисторе  в диапазоне 5-8В. Затем нажмём кнопку « в диапазоне 5-8В. Затем нажмём кнопку « ». Для стабилизации теплового режима необходимо подождать две минуты, после чего определить падение напряжения на проволоке ». Для стабилизации теплового режима необходимо подождать две минуты, после чего определить падение напряжения на проволоке  Опыт был повторён пять раз для пяти различных значений Опыт был повторён пять раз для пяти различных значений  (см. Таблица 2). (см. Таблица 2).
Оценим погрешность результатов измерения, используя формулы для вычисления абсолютной и относительной погрешностей прямых и косвенных измерений (9-11):   (10) (11) Где А – измеряемая величина,  – её среднестатистическое значение, – её среднестатистическое значение,  – коэффициент Стьюдента, S0 – среднеквадратичное отклонение от среднего значения, – коэффициент Стьюдента, S0 – среднеквадратичное отклонение от среднего значения,  - приборная погрешность, - приборная погрешность,  – абсолютная погрешность косвенного измерения, – абсолютная погрешность косвенного измерения, 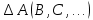 - абсолютная погрешность величины А(B,C,…), - абсолютная погрешность величины А(B,C,…), 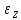 – относительная погрешность. – относительная погрешность.Получим, что 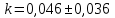 . Эксперимент проводился при 298 . Эксперимент проводился при 298 , нормальном атмосферном давлении, а согласно таблице коэффициента теплопроводности воздуха (см. Таблица 3 – источник: https://mash-xxl.info/tabs/217/), значение , нормальном атмосферном давлении, а согласно таблице коэффициента теплопроводности воздуха (см. Таблица 3 – источник: https://mash-xxl.info/tabs/217/), значение  , что входит в полученный доверительный интервал (при доверительной вероятности , что входит в полученный доверительный интервал (при доверительной вероятности  ). ).  Таблица 3. Вывод: Данный способ измерений позволяет оценить значение коэффициента теплопроводности воздуха, но погрешность результата велика. Это может быть вызвано конструктивными особенностями установки и порядком проведения эксперимента: температура самопроизвольно менялась в диапазоне порядка 1-го градуса (в лаборатории открывали окно, общая температура помещения снижалась, а значит, уже менее нагретый воздух попадал в вентиляционную систему установки); косвенные измерения температуры нити не могли обеспечить нужной точности из-за малых изменений сопротивления при изменениях температуры; двух минут, возможно, не достаточно для стабилизации теплового режима. |