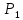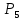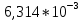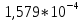Контрольная. 5 Бочаров. Отчет по лабораторной работе 5 по теме
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГАОУ ВО «Крымский федеральный университет имени В. И. Вернадского» Физико-технический институт Кафедра компьютерной инженерии и моделирования Отчет по лабораторной работе №5 по теме: “Расчет надежности КС” по дисциплине "Компьютерные системы" Выполнил студент 4 курса Группы ИВТ-б-з-181(1) Бочаров Ю.Е Проверила: Руденко М.А. Симферополь, 2022 Цель: Рассчитать надежность вычислительной системы с частичным контролем оборудования и периодическими профилактическими испытаниями. Исходные данные:  Рисунок 1 – Граф надежности устройства Si – состояния системы; S1 - система работоспособна; S2 - в системе обнаружен отказ; S3 - состояние необнаруженного отказа; S4 - состояние выполнения профилактических испытаний; S5 - в системе установлен скрытый отказ в результате профилактических испытаний. Таблица 1 Исходные данные
0 – интенсивность потока отказов; пф – интенсивность профилактических испытаний; пф - интенсивность профилактики; H – интенсивность восстановления; g – доля контролируемого оборудования; Теоретическая часть: Работоспособность системы или отдельных ее частей в процессе эксплуатации может быть нарушена в результате отказа аппаратуры – выхода из строя элементов или соединений между ними. Перед разработчиком технических средств стоит задача повышения надежности создаваемой аппаратуры. Надежность системы определяется вероятностью безотказной работы, т.е. вероятностью того, что при определенных условиях эксплуатации в заданный интервал времени не произойдет одиночного отказа. Выражение для вычисления безотказной работы:  , где t – интервал времени; , где t – интервал времени; i – интенсивность отказов i-го блока; m – число блоков ВС; Для повышения надежности ВС можно использовать резервирование ее элементов. Однако этот прием приводит к существенному увеличению стоимости системы. В нашем случае рассчитывается вероятность безотказной работы системы с частичным контролем оборудования и профилактическими испытаниями. Выполнение работы:
Сначала составим уравнение Колмогорова:   ; ; ; ;   Далее выразим вероятности:    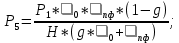 P1 определяет стационарную вероятность нахождения ВС в состоянии S1. 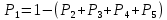 ; ;Вероятность работоспособного состояния для системы находится по формуле:  В нашем случае (при k=3): 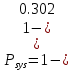 . .Результаты занесем в таблицу:
Найдем следующие значения: S1_2 =  = 0,455; = 0,455;S1_3 =  = 0,455; = 0,455;S1_4 =  = 0,5; = 0,5;S2_1 = H = 1,2; S3_2 =  = 0,455; = 0,455;S3_5 =  = 0,5; = 0,5;S4_1 =  = 0,69; = 0,69;S5_4 = H =1,2; Для расчета надежности будем использовать программу DIFUR. Устанавливаем вероятность начального состояния для S1 = 1:  Рисунок 2 Начальное состояние S1 Заполняем полученными ранее значениями матрицу переходов: 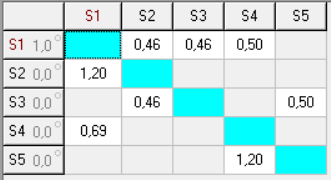 Рисунок 3 Матрица переходов  Рисунок 4 Граф переходов  Рисунок 5 Вероятность переходов Для достижения стационарного состояния потребовалось примерно 30 шагов (Т = 9), далее значения Рi не меняются.  Рисунок 6 График показывающий, что наступил установившийся режим По графику видим, что поглощающим является Р4, нам нужно изменить значения так, чтобы вероятность Р1 была больше других (вероятность состояния, при котором система будет работоспособна). Занесем полученные значения в таблицу и сравним с результатами аналитического расчета:
Откорректируем показатели (кроме 0) и добавим их в таблицу:
Изменяя пф, H и g, нужно помнить, что это повлечет за собой увеличение стоимости. Повторяем вычисления с учетом изменений: S1_2 =  = 0,9; = 0,9;S1_3 =  = 0,009; = 0,009;S1_4 =  = 0,05; = 0,05;S2_1 = H = 2; S3_2 =  = 0,9; = 0,9;S3_5 =  = 0,05; = 0,05;S4_1 =  = 0,99; = 0,99;S5_4 = H = 2; Занесем новые показания в матрицу переходов: 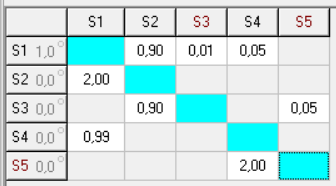 Рисунок 7 Матрица переходов 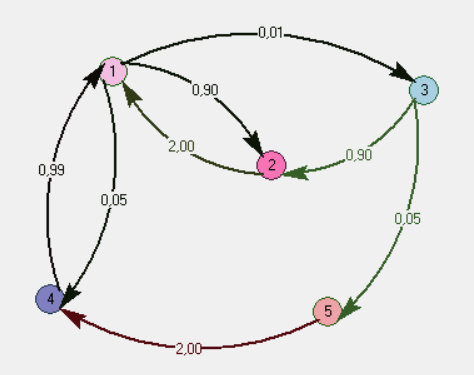 Рисунок 8 Граф переходов 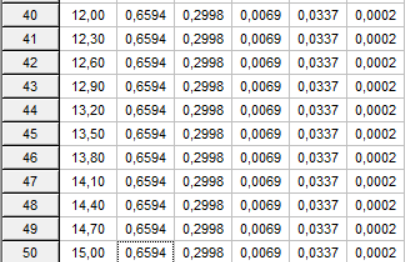 Рисунок 9 Вероятность переходов  Рисунок 10 График показывающий, что наступил установившийся режим Теперь, как и требовалось, поглощающим является состояние S1. Кроме корректировки значений мы можем изменять канальность (при выполнении лабораторной работы №4 было решено использовать 3 канала): 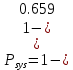 ; ;Добавим еще каналы и проследим зависимость: 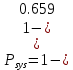 ; ;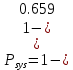 ; ;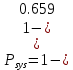 ; ;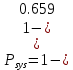 ; ;Из результатов видно, что увеличение количества каналов приводит к увеличению 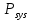 . Таким образом можно получить требуемую вероятность. . Таким образом можно получить требуемую вероятность.Добавим в таблицу новые значения и 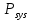 для 5 каналов: для 5 каналов:
Вывод: В ходе выполнение лабораторной работы мы рассчитали надежность вычислительной системы. Для машинного расчета была использована программа DIFUR. При вычислениях надежности системы с начальными данными, мы получили неудовлетворительные результаты, вероятность Р1 была равна 0,302, а 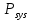 = 0,659. После некоторых корректировок значение Р1 увеличилось до 0,659, а = 0,659. После некоторых корректировок значение Р1 увеличилось до 0,659, а 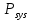 до 0,995. Поставленная задача повышения надежности компьютерной системы выполнена. до 0,995. Поставленная задача повышения надежности компьютерной системы выполнена. |