лаба по физике маятник Обербека. Маятник Обербека. Отчет по лабораторной работе Маятник Обербека
 Скачать 298.82 Kb. Скачать 298.82 Kb.
|
|
Пермский национальный исследовательский политехнический университет Факультет химических технологий, промышленной экологии и биотехнологий Отчет по лабораторной работе «Маятник Обербека» Выполнила студентка группы ХТ2‑20‑1б Евдокимова Мария Александровна Пермь, 2020 Введение. Данная лабораторная работа посвящена исследованию вращательного движения, момента инерции c помощью маятника Обербека. Маятник Обербека – лабораторное устройство, которое особенно актуально при изучении динамики вращательного движения относительно неподвижной оси. На примере работы маятника можно рассмотреть динамические характеристики вращательного движения твердого тела, такие как момент силы, момент инерции. Создателем маятника является немецкий физик Антон Обербек (Anton Oberbeck, 1846-1900). В лабораторной работе проводятся измерения движения маятника, находится его момент инерции, оценивается влияние трения на движение. Установка помогает обучаемым глубже понять основные физические закономерности и приобрести элементарные навыки проведения экспериментов. Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. Моме́нт ине́рции — скалярная физическая величина, мера инерции во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Цель работы: изучение основного закона динамики вращательного движения, определение момента инерции системы грузов. Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, два круглых груза, груз наборный, нить длиной 55 см с крючком (синяя), измерительная система ИСМ-1 (секундомер), пластиковый фиксатор. 1.1 Краткая теория Основной закон динамики вращательного движения твердого тела относительно неподвижной оси 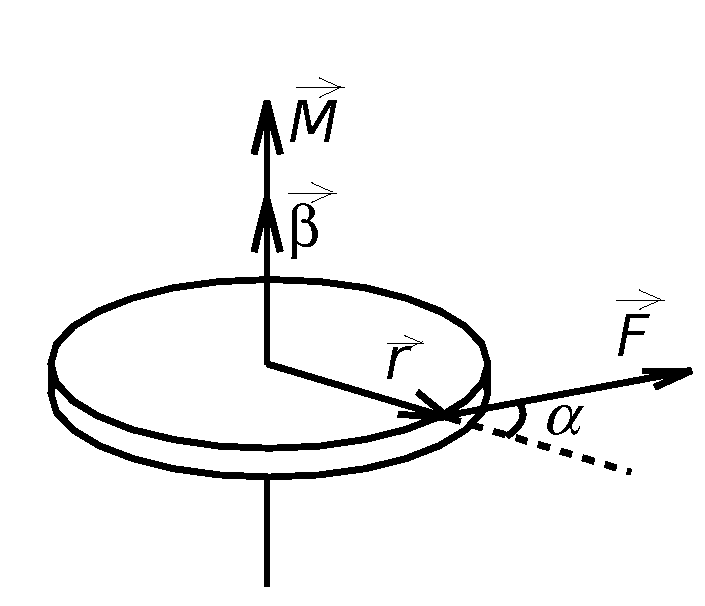 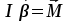 (1) (1)связывает кинематическую характеристику движения – угловое ускорение 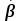 с динамическими характеристиками – моментом силы с динамическими характеристиками – моментом силы 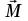 и моментом инерции I(рис. 1). и моментом инерции I(рис. 1).Угловое ускорение характеризует изменение угловой скорости во времени и направлено, как и момент силы, вдоль оси вращения. Рис. 1. Момент M силы F 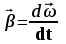 . (2) . (2)Угловое ускорение связано с касательной составляющей линейного ускорения аτточки вращающегося тела соотношением 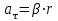 , (3) , (3)где r –- кратчайшее расстояние от этой точки до оси вращения. Моментом силы в общем случае называют векторную величину 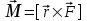 , (4) , (4)где 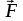 – сила, лежащая в плоскости, перпендикулярной оси вращения; – сила, лежащая в плоскости, перпендикулярной оси вращения; 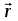 – вектор, соединяющий точку на оси c точкой приложения силы. – вектор, соединяющий точку на оси c точкой приложения силы.В уравнении (1) 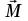 – сумма составляющих моментов сил вдоль направления оси вращения. – сумма составляющих моментов сил вдоль направления оси вращения.Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δmi, на которые мысленно разбито тело, на квадрат их расстояний до оси вращения I = Σ Δmiri . (5) Выражая Δmi через плотность тела: Δmi =ρ ΔVi,где ΔVi – элементарный объем тела, и переходя к пределу при ΔVi → 0, получим 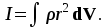 (6) (6)Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр, I= т l2 / 12 . Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. Теорема Штейнера устанавливает связь между моментом инерции Iс твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой I = Iс + mа2 , (7) где а – расстояние между осями, m – масса тела. В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m1, что дает возможность изменять момент инерции маятника. Грузы m1 устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения. 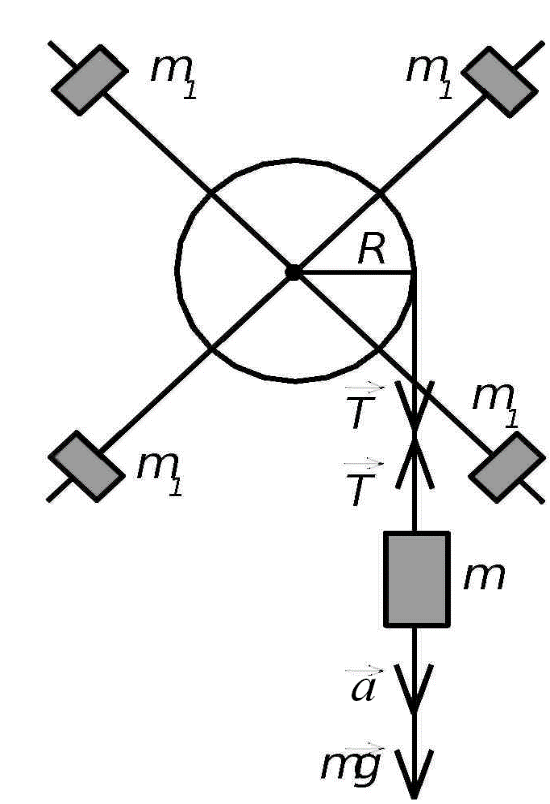 Рис. 2. Маятник Обербека К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует 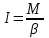 . (8) . (8)Основной закон динамики вращения (II закон Ньютона для вращательного движения): Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение. Момент силы М, создающийся силой натяжения нити, исходя из (4) 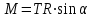 , (9) , (9)где α – угол между вектором 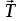 и отрезком Rна рис. 2, равный 90°; sin α= 1. и отрезком Rна рис. 2, равный 90°; sin α= 1.Запишем второй закон Ньютона для поступательного движения груза mв проекции на направление ускорения а, 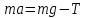 . (10) . (10)В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т. Из (9) и (10) получим 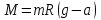 . (11) . (11)Т 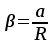 ангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима. ангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима. Тогда из (3) следует , (12) 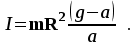 (13) (13)Подставляя (11)и(12)в (8), получим Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости. 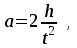 (14) (14)где h – путь, пройденный грузом т за время t. В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь h=2πR . (15) Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника 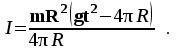 (16) Момент инерции маятника Обербека будет изменяться при изменении расстояния rот оси вращения маятника до центров грузов массами m1, перемещаемых вдоль стержней. Согласно теореме Штейнера (7) 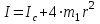 , (17) , (17)где Ic – момент инерции всей вращающейся части маятника при условии, что центры грузов m1находились бы на оси вращения. Из (17) следует, что зависимость 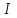 от от 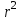 – линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции. – линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. Описание экспериментальной установки, её особенности.  1- 9-переключатели 10- стойка 11- блок 12- стержень 13- пластиковый фиксатор 14-два круглых груза 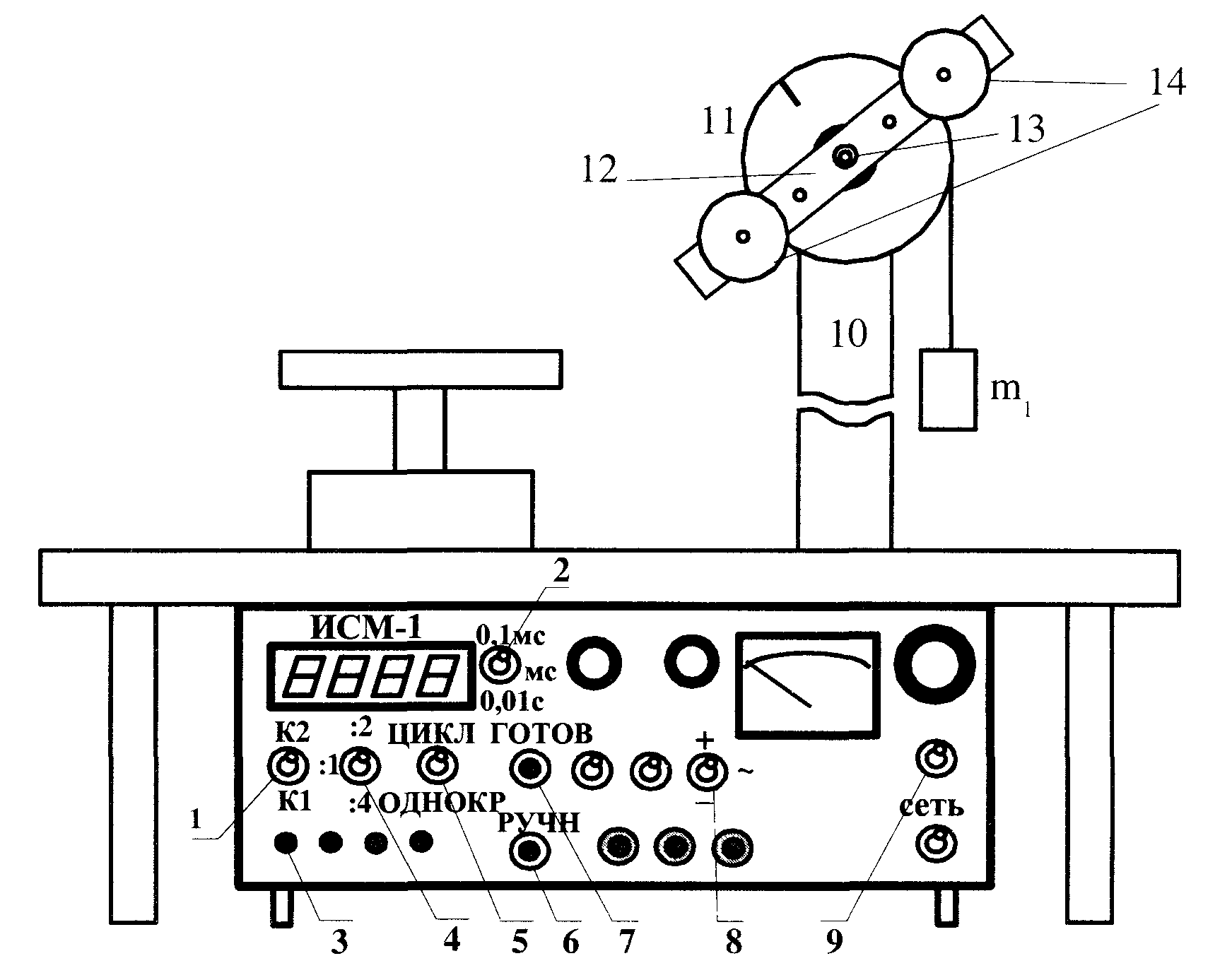 Рис. 2. Маятник Обербека на модуле ЛКМ-3 Маятник Обербека монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ-3 (рис. 2). К блоку радиусом 25 мм прикрепляют нить, к концу которой подвешивают наборный груз массой m1 = 100 - 200 г. На ось блока через среднее отверстие надевают стержень 12 и закрепляют его пластиковым фиксатором 13. Вращая стержень накручивают на блок нить и поднимают груз так чтобы он не касался стержня. При опускании груза нить приведет во вращательное движение стержень. После полного раскручивания нити стержень, продолжая вращательное движение, накрутит нить на блок и поднимет груз. При этом вращательное движение прекратится - система перейдет в начальное состояние. Время опускания и подъема груза (период колебаний маятника Обербека) зависит от многих параметров установки: длины нити, массы груза m1, момента инерции стержня и блока, радиуса блока (от сил трения, толщины и массы нити, которыми мы в данной работе пренебрегаем). Все эти допущения в дальнейшем скажутся на наших результатах. Конструкция прибора позволяет изменять момент внешних сил и момент инерции системы I. Момент внешних сил изменяется с изменением массы подвешенного к нити груза или при перенесении нити с одного шкива на другой. Момент инерции можно изменять, перемещая грузы m0 , по стержням крестовины. Результаты исследования. Таблица 1
В таблице 1 представлены результаты серии из пяти экспериментов по определению момента инерции стержня. Все опыты проведены в одинаковых условиях; разброс значений вызван неконтролируемыми факторами и определяется, как случайная погрешность. Время t поворота отличается. Каждые 5 значений различны. Это может быть связано с тем, что мы могли случайно толкнуть маятник, который бы быстрее или же ,наоборот, медленнее прошел 1 оборот. Мы провели 5 измерений времени вращения маятника. Рассчитаем момент инерции для каждого измерения (радиус маятника 25 мм): I= 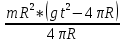 = = 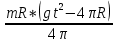 (1) (1)I1= 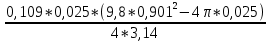 = 1,658*10-3 кг-м2 = 1,658*10-3 кг-м2I2= 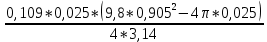 = 1,672*10-3 кг-м2 = 1,672*10-3 кг-м2I3= 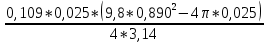 = 1,616*10-3 кг-м2 = 1,616*10-3 кг-м2I4= 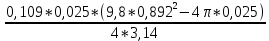 = 1,624*10-3 кг-м2 = 1,624*10-3 кг-м2I5= 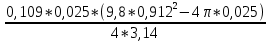 = 1,700*10-3 кг-м2 = 1,700*10-3 кг-м2Рассчитаем абсолютную и относительную погрешности помощи метода Стьюдента: 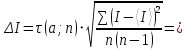 2,78 ⋅ 2,78 ⋅ 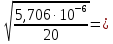 0,05 *10-3 0,05 *10-3 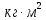 ε I = (ΔI/ < I >)*100% =(4,696*10-5/1,654*10-3)*100%=3% 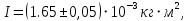 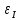 = 3 % при α = 0,95 = 3 % при α = 0,95 В результате мы получили достаточно точное значение момента инерции с погрешностью 3%. Но так как мы не учитывали массу и толщину нити, которые на практике увеличивали время прохождения полного оборота, То погрешность всё же есть. Также мы не учитывали силы трения в подшипниках оси блока и сопротивление воздуха, которые тоже замедляли время полного оборота. Измерение момента инерции маятника Обербека в зависимости от положения грузов на стержне. Таблица 2
I= 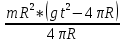 = = 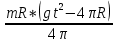 I1= 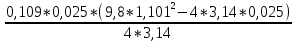 = 0,0025 кг-м2 = 0,0025 кг-м2I2 = 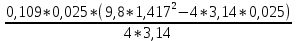 = 0,0042 кг-м2 = 0,0042 кг-м2I3 = 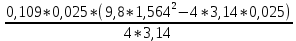 = 0,0051 кг-м2 = 0,0051 кг-м2I4 = 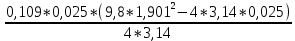 = 0,0076 кг-м2 = 0,0076 кг-м2I5 = 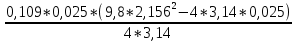 = 0,0098 кг-м2 = 0,0098 кг-м2I6 = 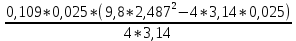 = 0,013 кг-м2 = 0,013 кг-м2I7 = 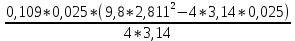 = 0,0167 кг-м2 = 0,0167 кг-м2При анализе зависимости значения момента инерции от расстояния между грузами выявилась следующая закономерность: чем больше расстояние между грузами, тем больше момент инерции (Таблица 2). По формуле 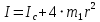 также можно понять, что момент инерции прямо пропорционален квадрату расстояний. также можно понять, что момент инерции прямо пропорционален квадрату расстояний. Построим график зависимости момента инерции Iот квадрата расстояния от оси вращения до центра грузов r2. 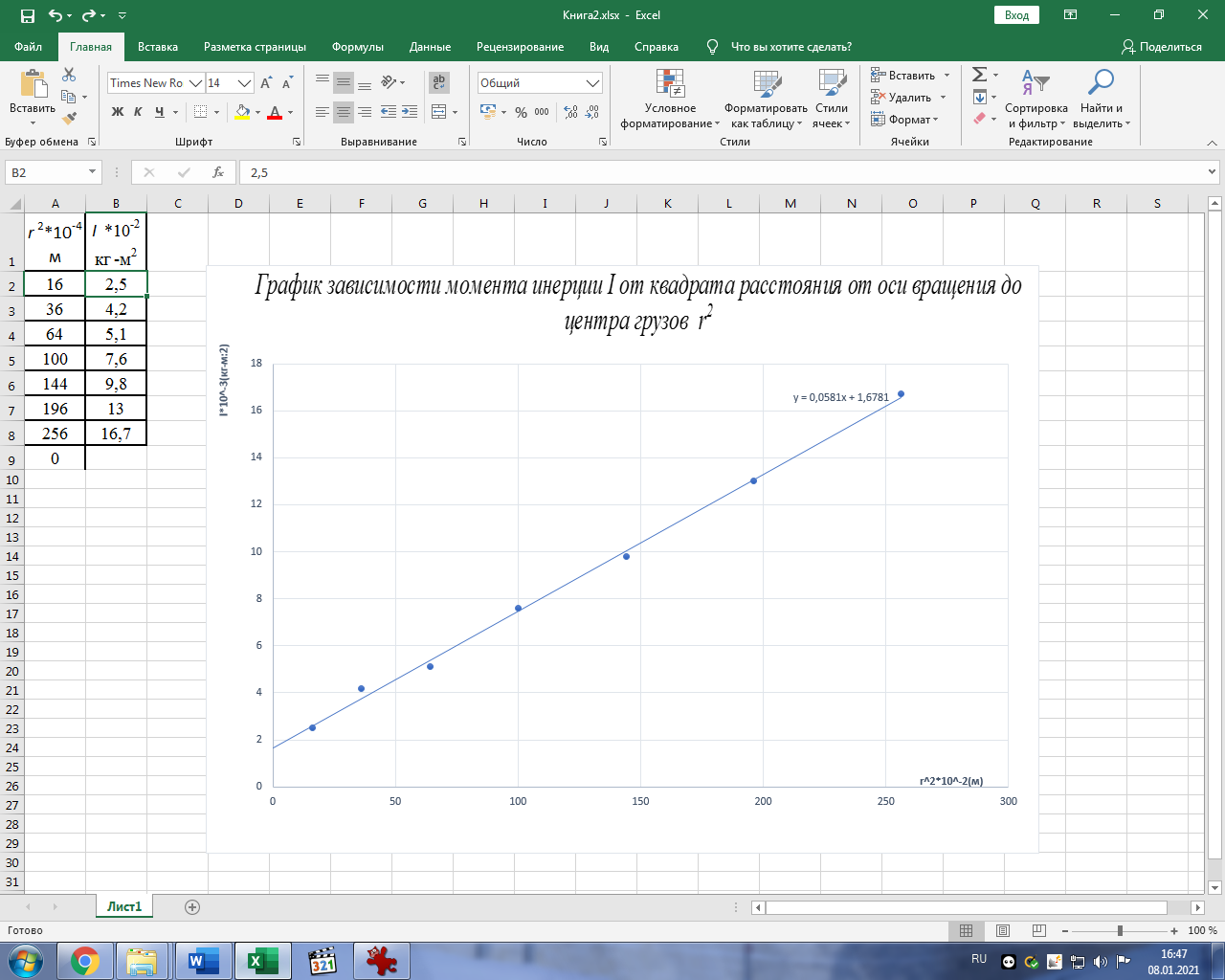 График зависимости момента инерции I от квадрата расстояния от оси вращения до центра грузов r2 По графику определим момент инерции маятника: IC=1,6781 кг∙м2 Это значение входит в пределы доверительного интервала для момента инерции. Анализ результатов. После проведения опытов и произведения расчётов над полученными результатами, был определён момент инерции с помощью маятника Обербека. При вычислении его расчётным способом не учитывались такие факторы, как сила трения в подшипниках оси блока, сопротивление воздуха, толщина нити, масса нити, впоследствии они дали отклонение в 1,5%. Пренебрежение действия этих сил и является главной причиной систематической погрешности измерения момента инерции. Результаты вычислений зафиксированы. Пришли к выводу, что при уменьшении радиуса вращения время вращения уменьшается. Построив график прямопропорциональности, заметим чем больше радиус шкива, тем больше момент инерции системы. Все опыты были проведены в одинаковых условиях. Разброс значений вызван неконтролируемыми факторами (случайная погрешность). При определении зависимости момента инерции от квадрата расстояния от оси вращения до центра грузов получилась линейная зависимость, что указывает на достоверность вычислений. 3.1 Методические погрешности. 1) Сила трения в подшипниках блока замедляет движение блока, вращение перестает быть «свободным». Это влияет на время оборота, и в последствии получатся не полностью достоверные значения с погрешностями. 2) Падение замедляется из-за действия силы трения о воздух. 3) Проскальзывание и нерастяжимость нити также могут привести к погрешности. Заключение. В результате выполнения данной лабораторной работы , я изучила основной закон динамики вращательного движения, определила момент инерции системы грузов.. Небольшие погрешности обусловлены тем, что присутствует сила упругости, сила трения нити о подшипник, сила трения в блоке, а также инертность блока. Чтобы свести эту погрешность к минимуму, измерения проводились несколько раз с выведением среднего результата. В ходе выполнения лабораторной работы я определила момент инерции стержня и блока, а также измерила момента инерции маятника Обербека в зависимости от положения грузов на стержне с учётом трения в подшипниках оси блока. Сравнила результаты, полученные в первом и втором опытах. Литература Методическое пособие. Общая физика, часть 1, механика. Лабораторный практикум. Под общей редакцией профессора Л.Н. Кротова. Издательство Пермского государственного технического университета, 2009. Стр.34-41 https://yandex.ru/images/search?text=%D0%BC%D0%B0%D1%8F%D1%82%D0%BD%D0%B8%D0%BA%20%D0%BE%D0%B1%D0%B5%D1%80%D0%B1%D0%B5%D0%BA%D0%B0%20%D0%BD%D0%B0%20%D0%BB%D0%BA%D0%BC%203&from=tabbar&pos=0&img_url=http%3A%2F%2F5fan.ru%2Ffiles%2F2%2F5fan_ru_11906_76f9b372e885658b9710a7fb3b5d5d2e.html_files%2F1.png&rpt=simage |
