Курсовая по АТЧ. Отношение порядка в кольце целых чисел
 Скачать 65.55 Kb.
|
|
ОТНОШЕНИЕ ПОРЯДКА В КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
1 Исследователя окружающего мира интересуют различные свойства объектов: свойства, относящиеся к отдельным объектам (например, "быть женщиной", "иметь форму правильного пятиугольника", "быть сделанным из металла", "быть голубым", "иметь низкую теплопроводность") и свойства, характеризующие связи между несколькими объектами (например, свойства "быть родственниками" и "быть больше" относятся к парам объектов, свойство "находиться между" - к тройкам объектов, свойство "располагаться в вершинах квадрата" - к четверкам объектов). Такие свойства принято называть отношениями. При этом свойства отдельных объектов называются унарными отношениями, свойства, относящиеся к парам объектов, - бинарными отношениями, свойства, относящиеся к наборам из n объектов, - n-арными отношениями. Ниже мы ограничимся рассмотрением лишь бинарных отношений. Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и n-арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. Широкое использование языка бинарных отношений легко объясняется - геометрический аспект теории бинарных отношений есть попросту теория графов. Введем необходимые определения. Определение 1.1. Декартовым произведением множеств X и Y называется множество X  Y всех упорядоченных пар (x, y) таких, что x X, y Y.Определение 1.2. Соответствием между множествами X и Y (или соответствием из X в Y) называется любое подмножество декартова произведения X Y. Если множества X и Y совпадают, то соответствие между множествами X и Y называют также бинарным отношением на множестве X.Пример 1.1. Пусть X ={a, b, c, d}, Y ={1, 2, 3, 4, 5}. Тогда множество кортежей α={(a, 1), (b, 2), (c, 3), (d, 4)} являются соответствием из X в Y. Отметим, что обычно соответствия задаются не путем указания подмножества α декартова произведения X Y , а путем указания свойства пар (x, y), принадлежащих этому подмножеству α. Например, отношение α= {(4, 4), (3, 3), (2, 2), (4, 2)} на множестве X = {4, 3, 2} можно определить как свойство "Делиться нацело" на этом подмножестве целых чисел.Хорошо известными примерами отношений из школьного курса математики являются: • на множестве целых чисел Z отношения "делиться", "делит", "равно", "больше", "меньше", "взаимно просты"; • на множестве прямых пространства отношения "параллельны", "взаимно перпендикулярны", "скрещиваются", "пересекаются", "совпадают"; • на множестве окружностей плоскости "пересекаются", "касаются", "концентричны". Факт принадлежности кортежа (x, y) соответствию α, часто обозначают с помощью так называемой инфиксной формы записи: xαy. Типичными примерами таких записей из курса математики являются: x > y, a = b, 8  4, m||l, a b и т. п.Отношения могут задаваться формулами: формулы y= x2+5x-6 или  задают бинарные отношения на множестве действительных чисел;формула x+y=любовь, задает бинарное отношение на множестве людей. Этому отношению принадлежит любая пара людей, между которыми существует любовь. Задание отношений в виде формул достаточно широко распространено. Об этом свидетельствуют многочисленные надписи на деревьях заборах или стенах домов типа: "Вася + Таня = любовь", увековечивающие принадлежность конкретной пары (Вася, Таня) отношению "любовь". Рассмотрим еще три формы представления бинарных отношений: матричное представление и два графических представления. В качестве носителя отношения для иллюстрирующих примеров будем использовать множество X = {a, b, c, d, e}. Вначале рассмотрим метод, восходящий к аналитической геометрии. Начертим пару взаимно перпендикулярных осей (OX - горизонтальная ось, а OY - вертикальная ось) и на каждой отметим точки, представляющие элементы множества X (рис. 1). 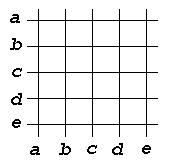 Рис. 1. Координатная сетка Считая метки a, b, c, d, e координатами точек на горизонтальной и вертикальной осях, отметим на плоскости точки с координатами (x, y) такими, что (x, y) . На рисунке 2 изображено множество точек, соответствующее отношению α= {(a, b), (a, c), (b, d), (c, e), (e,b), (e, e)}. 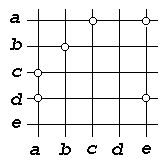 Рис. 2. Бинарное отношение α Другой широко распространенный способ представления отношений основан на использовании ориентированных графов. При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x, y) отношения α дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y. Граф бинарного отношения α изображен на рисунке 3. 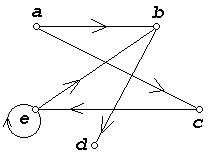 Рис. 3. Граф бинарного отношения Для бинарных отношений, определенных на конечных множествах, часто используется матричный способ задания. Пусть на некотором конечном множестве X задано отношение a. Упорядочим каким-либо образом элементы множества X ={x1, x2,..., xn} и определим матрицу отношения A =[aij] следующим образом: 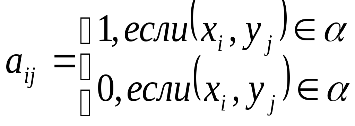 Таким образом, матрица отношения α, представленного графом на рисунке 3, имеет вид 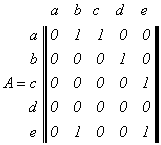 Часто матрицу отношения называют булевой, чтобы подчеркнуть, что ее элементами являются только Отношение нестрогого (рефлексивного) частичного порядка ({\displaystyle \preccurlyeq }  ) на множестве {\displaystyle X} — это бинарное отношение, для которого при любых {\displaystyle a,b,c} из {\displaystyle X} выполнены следующие условия[2]:Рефлексивность: {\displaystyle a\preccurlyeq a} .Антисимметричность: если {\displaystyle a\preccurlyeq b} и {\displaystyle b\preccurlyeq a} , то {\displaystyle a=b} .Транзитивность: если {\displaystyle a\preccurlyeq b} и {\displaystyle b\preccurlyeq c} , то {\displaystyle a\preccurlyeq c} .Удобно также дополнительно определить для отношения {\displaystyle \preccurlyeq } отношение строгого (антирефлексивного) порядка ({\displaystyle \prec } ) на том же множестве[1]:{\displaystyle a\prec b} , если {\displaystyle a\preccurlyeq b} и при этом {\displaystyle a\neq b.} Свойства строгого отношения отличаются от свойств нестрогого: Антирефлексивность: {\displaystyle a\not \prec a} ;Асимметричность: если {\displaystyle a\prec b} , то {\displaystyle b\not \prec a} ;Транзитивность: если {\displaystyle a\prec b} и {\displaystyle b\prec c} , то {\displaystyle a\prec c} .2-е свойство не является независимым, оно следует из антирефлексивности и транзитивности. Поэтому отношение является отношением строгого порядка тогда и только тогда, когда оно антирефлексивно и транзитивно. Множество {\displaystyle X} , на котором введено отношение строгого или нестрогого порядка, называется частично упорядоченным. Если к тому же для любых элементов {\displaystyle a\neq b} дополнительно выполняется одно из условий: {\displaystyle a\prec b} или {\displaystyle b\prec a,} то порядок называется линейным, а множество — линейно упорядоченным[2]. | ||||||||||||||||||||||||