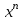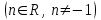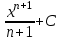Проект. первообразная1. Первообразная. Пусть на некотором промежутке задана функция. Функция называется первообразной
 Скачать 88.53 Kb. Скачать 88.53 Kb.
|
|
Первообразная. Пусть на некотором промежутке 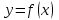 . Функция . Функция 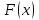 называется первообразной для называется первообразной для 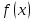 на этом промежутке, если для всех на этом промежутке, если для всех Например, функция 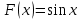 является первообразной для функции является первообразной для функции 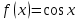 , так как , так как 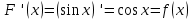 . .Но функция 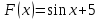 тоже является первообразной для функции тоже является первообразной для функции 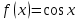 , так как , так как 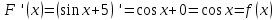 . .Аналогично, функции 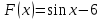 , , 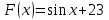 будут первообразными для функции будут первообразными для функции 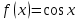 . .Основное свойство первообразной Если функция 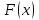 есть первообразная для функции есть первообразная для функции 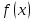 на некотором промежутке на некотором промежутке 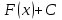 , где С – произвольная постоянная, , где С – произвольная постоянная, 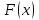 - также является первообразной для функции - также является первообразной для функции 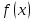 на промежутке на промежутке 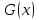 функции функции 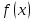 на промежутке на промежутке 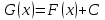 . .Геометрически основное свойство первообразных можно интерпретировать так: графики всех первообразных данной функции 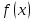 получаются из любого из них путем параллельного переноса вдоль оси получаются из любого из них путем параллельного переноса вдоль оси Три правила нахождения первообразных: 1.Если 2. Если 3. Если Таблица первообразных:
Пример 1. Докажем, что функция а) Найдем производную функции б) Найдем производную функции Так как  для всех для всех Пример 2. Используя таблицу первообразных, найдем одну из первообразных для функции: а) 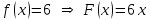 ; ;б) 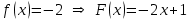 ; ;в) 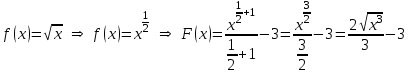 ; ;г) 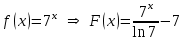 . .Пример 3. Для функции а) Запишем общий вид первообразных для данной функции: Таким образом, искомая первообразная имеет вид Пример 4. Найдем общий вид первообразных для функций: а) Для функции б) По правилу 3 одной из первообразных для функции Задания для самостоятельного выполнения: 1.Найдите первообразную функции, график которой проходит через заданную точку и сравните с ответом: а) б)  , , в) г) д) е) 2. Указав правило нахождения первообразных, найдите множество первообразных функции: а) г) ж) |