Высшая математика. Элементы высшей алгебры и геометрии». 2 задание Высшая математика. Элементы высшей алгебры и геометрии. По учебному курсу Высшая математика
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» ФГБОУ ВО «Тольяттинский государственный университет»
Практическое задание №_1__ по учебному курсу «Высшая математика. Элементы высшей алгебры и геометрии» (наименование учебного курса) Вариант ____ (при наличии)
Тольятти 2023 Раздел № 2. векторная алгебра Задача 1Вариант 7 По координатам вершин пирамиды АВСD средствами векторной алгебры найти: 1) длины ребер АВ и АС; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) проекцию вектора  на на  ; ; 5) объем пирамиды.
   Длины ребер АВ и АС: Длины ребер АВ и АС:  = =  b-xa)2 + (yb-ya)2 + (zb-za)2 = b-xa)2 + (yb-ya)2 + (zb-za)2 =  (1-2)2 + (3-3)2 + (6-2)2 = (1-2)2 + (3-3)2 + (6-2)2 = (-1)2+ 02 +42 = (-1)2+ 02 +42 =      = =  = =   4.123 4.123 = =  c-xa)2 + (yc-ya)2 + (zc-za)2 = c-xa)2 + (yc-ya)2 + (zc-za)2 =  (0-2)2 + (4-3)2 + (2-2)2 = (0-2)2 + (4-3)2 + (2-2)2 = (-2)2+ 12 +02 = (-2)2+ 12 +02 =    = =  4+1+0 = 4+1+0 =  5 5  2.236 2.236Угол между ребрами АВ и АС: arccos  = arccos = arccos  = arccos = arccos   (1.352 (1.352  ) )  77.471 77.471  Площадь грани АВС: 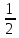  2 + 2 +  2 + 2 +  2 = 2 = 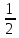   2 + 2 +  2 + 2 + 2 = 2 = 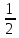  (-4)2 + 82 + (-1)2 = (-4)2 + 82 + (-1)2 =  4.5 4.5Проекцию вектора  на на  : :Объем пирамиды:  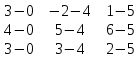 = =   = =  3 3  – (-6) – (-6)  + (-4) + (-4)  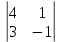 = =  3 3  (-2) – (-6) (-2) – (-6)  (-15) + (-4) (-15) + (-4)  (-7) = (-7) =  -6 -90 +28 = -6 -90 +28 =  -68 = -68 =  Задача 2 Вариант 7 Составить уравнение плоскости Р, проходящей через точку А перпендикулярно вектору   . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости , проходящей через точки А, В, С. Найти угол между плоскостями Р и , проходящей через точки А, В, С. Найти угол между плоскостями Р и  . Найти расстояние от точки Dдо плоскости Р. . Найти расстояние от точки Dдо плоскости Р.
BC = (2-7, 1-0, 4-1) = (-5, 1, 3). (-5) * (x-5) + 1 * (y-1) + 3 * (z-0) = 0 , -5x+y+3z+24 = 0   x – 5 y – 1 z – 0 x – 5 y – 1 z – 0 7 – 5 0 – 1 1 – 0 = 0 2 – 5 1 – 1 4 – 0   x – 5 y – 1 z – 0 x – 5 y – 1 z – 0 2 -1 1 = 0 -3 0 4 (x-5) (-1*4-1*0) – (y-1) (2*4-1*(-3)) + (z-0) (2*0-(-1)*(-3)) = 0 (-4)(x-5) + (-11)(y-1) + (-3)(z-0) = 0 -4x – 11y – 3z + 31 =0  = =  = = 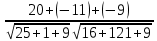 = =  = = 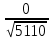 = 0 = 0 = 900 = 900 d = d =  = =  = =  = =  * *   4.3863112095925505 4.3863112095925505Задача 3Прямая l задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой 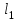 , проходящей через точку М параллельно прямой l,и вычислить расстояние между ними. Найти проекцию точки М на прямую l и точку пересечения прямой l и плоскости Р. , проходящей через точку М параллельно прямой l,и вычислить расстояние между ними. Найти проекцию точки М на прямую l и точку пересечения прямой l и плоскости Р. |
