КР 3 Графы_11. Построим изображение графа
 Скачать 490.71 Kb. Скачать 490.71 Kb.
|
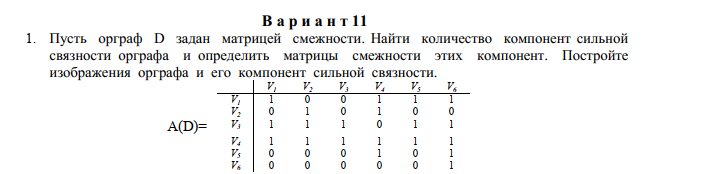 Построим изображение графа 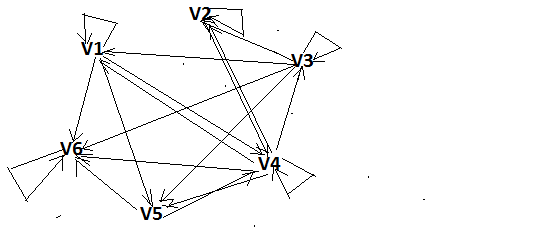 Видим, что из 6 вершины выходит стрелка только в 6. Значит, нельзя из 6 попасть в 1, например и граф не сильно связный. Далее видим, что из 4 вершины можно попасть во все, и из любой вершины кроме 6 можно попасть в 4 по стрелкам. Из 1,2,4,5 - по дуге, а из 3 по паре дуг 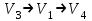 . Значит, граф без 6 вершины сильно связный. У нас не менее 2 компонент связности и мы нашли эти 2 компоненты. Первая из 6 первых 5 вершин и вторая из 6. . Значит, граф без 6 вершины сильно связный. У нас не менее 2 компонент связности и мы нашли эти 2 компоненты. Первая из 6 первых 5 вершин и вторая из 6. Их матрицы смежности:
И
Изображения компонент сильной связности: 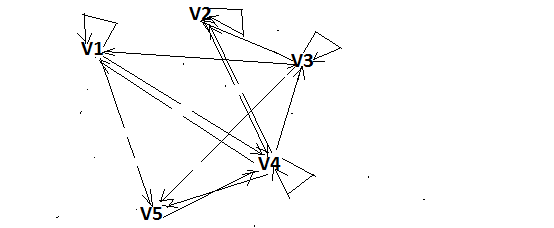  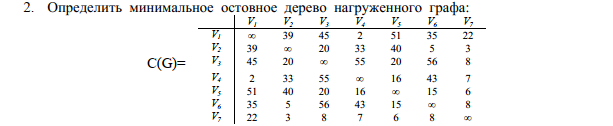 Решение: Матрица весов дуг симметрична. То есть граф неориентированный, и можно просто ставить ребра без стрелок вместо двух дуг. Действуем жадным алгоритмом. Выбираем произвольным образом вершину. Пусть это будет 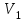 . Выбираем ребро минимального веса с ней. Это . Выбираем ребро минимального веса с ней. Это 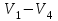 ,веса 2). Получили подграф ,веса 2). Получили подграф 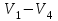 . .Среди всех не взятых еще ребер, которые выходят из 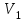 или или 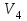 , ищем ребро наименьшего веса. Это ребро , ищем ребро наименьшего веса. Это ребро 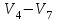 весом 7. Его прибавление не добавляет циклов. Добавляем. весом 7. Его прибавление не добавляет циклов. Добавляем. Получаем на данном шаге пока подграф 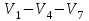 . .Среди всех невыбранных ребер, с вершинами в выбранных вершинах ищем ребро минимального веса. Это ребро 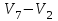 весом 3). Его прибавление не создает циклов, прибавляем. Получили пока поддерево весом 3). Его прибавление не создает циклов, прибавляем. Получили пока поддерево 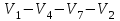 . .Среди всех невыбранных ребер, с вершинами в выбранных вершинах ищем ребро минимального веса. Это ребро 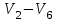 весом 5 добавление не создает циклов, добавляем. Получили поддерево весом 5 добавление не создает циклов, добавляем. Получили поддерево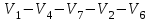 . Среди всех невыбранных ребер, с вершинами в выбранных вершинах ищем ребро минимального веса. Это ребро . Среди всех невыбранных ребер, с вершинами в выбранных вершинах ищем ребро минимального веса. Это ребро 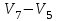 весом 6. Его прибавление не создает циклов. весом 6. Его прибавление не создает циклов.Прибавляем, получаем поддерево: 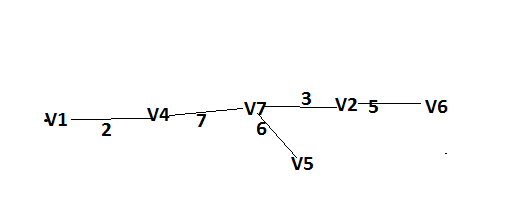 В нём не хватает только 3 вершины. Чтобы не получить цикл для ускорения процесса сразу ищем самое легкое ребро из вершины 3 (потому что на данном этапе остальные вершины уже выбраны и следующее добавленное точно будет из вершины 3). Самое легкое такое ребро это ребро 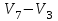 весом 8. Добавляем его и получаем требуемое остовное дерево: весом 8. Добавляем его и получаем требуемое остовное дерево: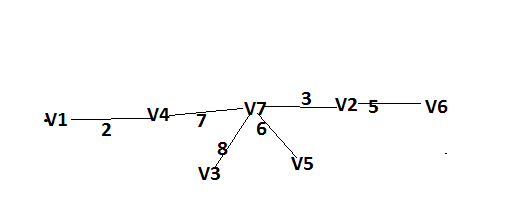 Считаем его вес 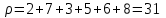 . . Решение: Используем алгоритм Дейкстры. Присваиваем вершинам временные метки из 1 строки таблицы
Рассматриваем первую смежную вершину 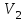 ( первую попавшуюся, где метка не бесконечность). ( первую попавшуюся, где метка не бесконечность).По 2 строке таблицы видим, что она смежна с вершинами 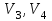 , ,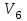 , ,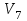 (то есть из неё есть дуга в эти вершины) (то есть из неё есть дуга в эти вершины)Считаем сумму расстояния до них и метки до вершины 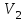 и сравниваем с текущими метками: и сравниваем с текущими метками: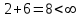 , меняем метку , меняем метку 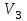 ; ; 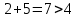 ; не меняем метку ; не меняем метку 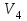 ; ;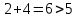 , не меняем метку , не меняем метку 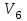 ; ;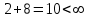 , не меняем метку , не меняем метку 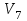 ; получаем на данном шаге метки: ; получаем на данном шаге метки:
Рассматриваем следующую смежную вершину 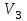 По 3 строке таблицы видим, что она смежна с вершинами 2,4,5,7( из не рассмотренных). Считаем сумму расстояния до них и метки вершины 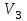 и сравниваем с текущими метками: и сравниваем с текущими метками: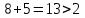 не меняем метку 2 вершины. не меняем метку 2 вершины.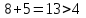 не меняем метку 4 вершины. не меняем метку 4 вершины.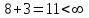 меняем метку 5 вершины. меняем метку 5 вершины.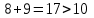 не меняем метку 7 вершины. Получаем на данном шаге метки: не меняем метку 7 вершины. Получаем на данном шаге метки:
Рассматриваем следующую смежную вершину 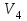 По 4 строке таблицы видим, что она смежна с вершинами 2,3,5,7 Считаем сумму расстояния до них и метки вершины 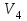 и сравниваем с текущими метками: и сравниваем с текущими метками: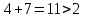 не меняем; не меняем;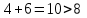 не меняем; не меняем;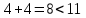 меняем метку 5 вершины. меняем метку 5 вершины.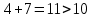 не меняем. Получаем на данном шаге метки: не меняем. Получаем на данном шаге метки:
Рассматриваем следующую вершину ну 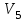 По 5 строке таблицы видим, что она смежна с вершинами 3,4,6,7 Считаем сумму расстояния до них и метки вершины 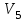 и сравниваем с текущими метками: и сравниваем с текущими метками: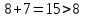 не меняем; не меняем;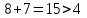 не меняем; не меняем;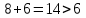 не меняем не меняем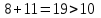 не меняем. Метки не изменились. не меняем. Метки не изменились.Рассматриваем последнюю вершину ну 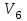 По 6 строке таблицы видим, что она смежна с вершинами 2,4,5 Считаем сумму расстояния до них и метки вершины 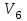 и сравниваем с текущими метками: и сравниваем с текущими метками: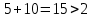 не меняем; не меняем;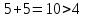 не меняем; не меняем;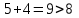 не меняем. Метки не изменились. По итоговой метке 7 вершины получаем, что кратчайший путь из не меняем. Метки не изменились. По итоговой метке 7 вершины получаем, что кратчайший путь из 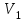 в в 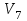 имеет длину 10. И имеет вид имеет длину 10. И имеет вид 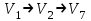 Не рассматривали ребра, входящие в V1 и выходящие из 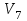 , так как если ходить по ним, путь из , так как если ходить по ним, путь из 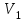 в в 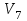 будет, очевидно, не самым кратчайшим. будет, очевидно, не самым кратчайшим. Найти максимальный поток и минимальны разрез в транспортной сети: 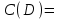
Решение: Все ребра идут у нас из вершины с меньшим номером в вершину с большим. Поэтому не будем ставить на них стрелки, и так понятно направление. Изобразим граф нашей транспортной сети: 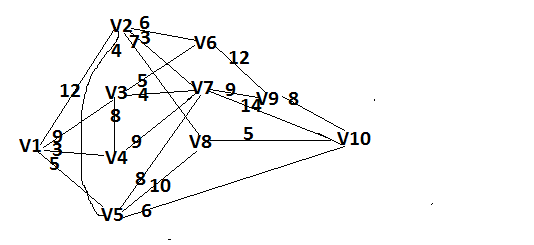 Источник 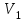 , сток , сток 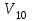 . .Рассматриваем путь 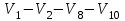 из ненасыщенных дуг. Максимальный поток по нему равен из ненасыщенных дуг. Максимальный поток по нему равен 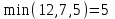 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 5. , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 5.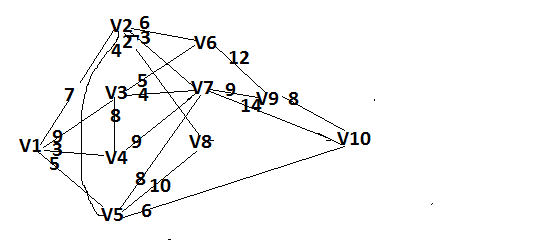 Берем путь 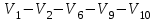 из ненасыщенных дуг. Максимальный поток по нему равен из ненасыщенных дуг. Максимальный поток по нему равен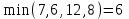 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 6. , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 6.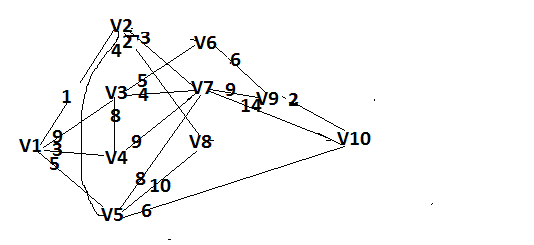 Берем путь 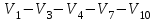 из ненасыщенных дуг. Максимальный поток по нему равен из ненасыщенных дуг. Максимальный поток по нему равен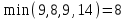 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 8 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 8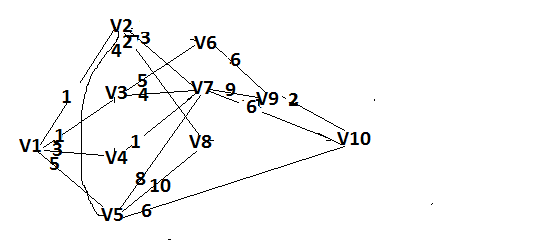 Берем путь 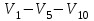 из ненасыщенных дуг. Максимальный поток по нему равен из ненасыщенных дуг. Максимальный поток по нему равен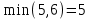 , пускаем такой поток, уменьшаем пропускную способность каждой дуги пути на 5 , пускаем такой поток, уменьшаем пропускную способность каждой дуги пути на 5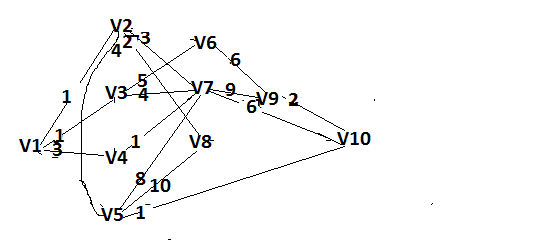 Берем путь 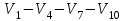 из ненасыщенных дуг. Максимальный поток по нему равен из ненасыщенных дуг. Максимальный поток по нему равен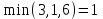 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 1 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 1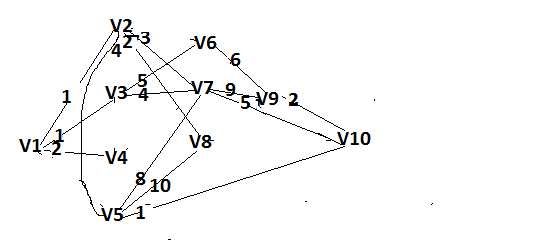 Берем путь 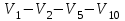 . Максимальный поток по нему равен . Максимальный поток по нему равен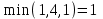 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 1 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 1Наконец берем путь 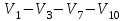 . Максимальный поток по нему равен . Максимальный поток по нему равен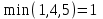 , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 1. , пускаем такой поток, уменьшаем пропускную способность каждой дуги на 1.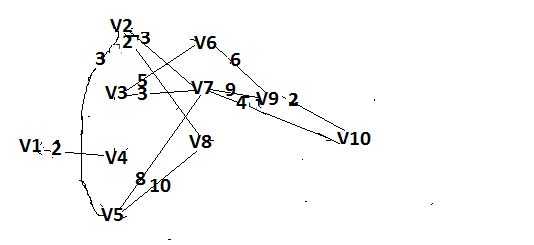 Больше нет путей из 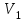 в в 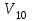 по ненасыщенным дугам. Процесс окончен. по ненасыщенным дугам. Процесс окончен. Максимальный поток равен сумме потоков на каждом шаге. 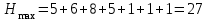 . .Находим минимальный разрез. Из нашего алгоритма выходит, что это 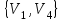 в одной доле и остальные вершины во второй. Считаем его пропускную способность (сумму пропускных способностей дуг, выходящих из первой доли во вторую в исходном графе). в одной доле и остальные вершины во второй. Считаем его пропускную способность (сумму пропускных способностей дуг, выходящих из первой доли во вторую в исходном графе).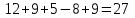 совпало. Пропускную способность ребра совпало. Пропускную способность ребра 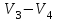 мы вычли, так как оно ведет из второй доли в первую. мы вычли, так как оно ведет из второй доли в первую.Ответ: максимальный поток равен 27.Он состоит из потоков: 5 по ветке 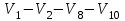 ; 6 по ветке ; 6 по ветке 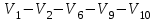 ; 8 по ветке ; 8 по ветке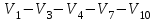 ; ;5 по ветке 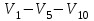 ; 1 по ветке ; 1 по ветке 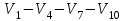 ; 1 по ветке ; 1 по ветке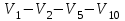 ; ;1 по ветке 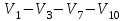 ; Минимальный разрез равен имеет пропускную способность 27 и состоит из вершин ; Минимальный разрез равен имеет пропускную способность 27 и состоит из вершин 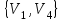 в одной доле и остальные вершины во второй в одной доле и остальные вершины во второй.  Решение: Граф 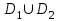 содержит те и только те вершины и ребра, что содержит хотя бы один из исходных графов. Можно считать, что второй граф тоже на тех же 4 вершинах вершинах, просто содержит те и только те вершины и ребра, что содержит хотя бы один из исходных графов. Можно считать, что второй граф тоже на тех же 4 вершинах вершинах, просто 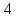 в нём изолированная) Получаем: в нём изолированная) Получаем: Добавили ребра 2-1 и 2-3. Ребра 3-1 и 3-2 и так уже были в 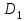 . Именно эти ребра и будут в графе пересечения . Именно эти ребра и будут в графе пересечения Задаем граф объединения списком ребер: 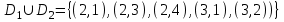 Представляем его матрицей смежности. В ней будет 4 строки и столбца. Представляем его матрицей смежности. В ней будет 4 строки и столбца. 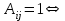 , в , в 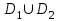 есть ребро из вершины есть ребро из вершины 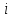 в вершину в вершину 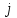 и ноль иначе. Получаем матрицу смежности: и ноль иначе. Получаем матрицу смежности: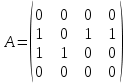 Затем строим матрицу инцидентности. Для этого пронумеруем все ребра графа следующим образом: 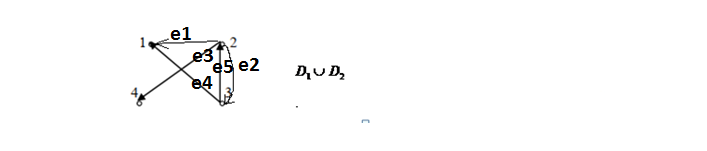 В матрице инцидентности будет 4 строки, соответствующих вершинам и 5 столбцов, соответствующих ребрам. В каждом столбце ставим -1 в строке вершины, из которой выходит соответствующее ребро, 1 – в которую входит и ноль в остальных строках. Получаем матрицу инцидентности: 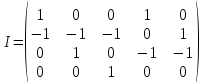 Определяем частичные полустепени исхода и захода вершин (сколько дуг выходит/входит).
Проверка: суммы в строках должны быть равны и равны количеству ребер. 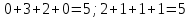 . Всё совпало. . Всё совпало.Строим какой-нибудь частичный граф: Для этого просто уберем часть ребер. К примеру, уберем только ребро 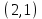 . Получим частичный граф: . Получим частичный граф: Строим какой-нибудь подграф. Для этого, например, уберем вершину 1 и все ребра, которые в неё заходят или из неё выходят. Получим:  Построим дополнительный орграф к последнему подграфу. Он будет состоять из всех ребер исходного графа, кроме тех, что принадлежат предыдущему подграфу. Получим:  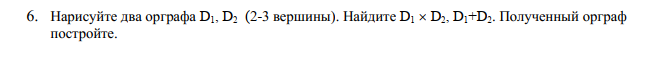 Решение: Возьмем следующие графы 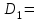 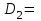 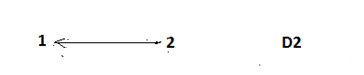 Находим их прямое произведение. В нем будут вершины 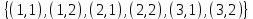 Смотрим , какие из них смежны. 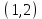 и и 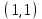 ; ; 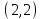 и и 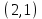 ; ; 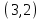 и и 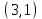 (так как в (так как в 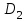 смежны вершины 2 и 1). смежны вершины 2 и 1).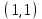 и и 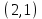 ; ; 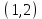 и и 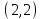 ; (так как в ; (так как в 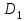 смежны вершины 1 и 2); смежны вершины 1 и 2);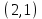 и и 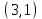 ; ; 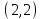 и и 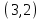 ; (так как в ; (так как в 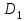 смежны вершины 2 и 3); смежны вершины 2 и 3);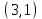 и и 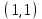 ; ; 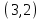 и и 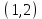 ; (так как в ; (так как в 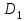 смежны вершины 3 и 1); смежны вершины 3 и 1);Получаем произведение: 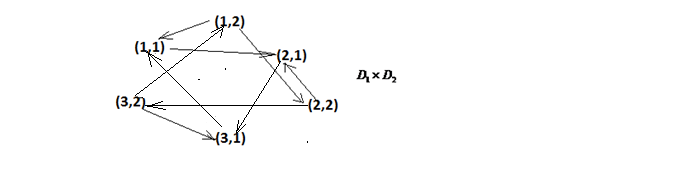 Сумма графов 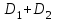 это то же что и их объединение, граф, который содержит все ребра, принадлежащие хотя бы одному из них. Получаем сумму: это то же что и их объединение, граф, который содержит все ребра, принадлежащие хотя бы одному из них. Получаем сумму: 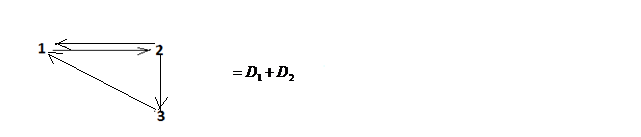 |