Квалификация. МУ-по-выполнению-ПР№3-Определение-координат-центра-тяжести-сложн. Практическая работа Определение координат центра тяжести сложной фигуры Цель работы
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Практическая работа № 3. Определение координат центра тяжести сложной фигуры Цель работы: Определить координаты центра тяжести сложной фигуры аналитическим способом Теоретическое обоснование. Практическая работа выполняется после изучения темы «Центр тяжести». Понятие центра тяжести неразрывно связано с законом всемирного тяготения, который утверждает, что все тела находящиеся на поверхности Земли или над ней, притягиваются к центру Земли с силой равно силе тяжести G=mg. Так как материальное тело можно рассматривать как систему материальных точек, жестко связанных между собой, следовательно, силы тяжести, действующие на материальные точки тела можно рассматривать как пространственную систему параллельных сил. Центром тяжести тела называется точка, через которую проходит линия действия равнодействующей сил тяжести материальных точек тела. Центр тяжести простейших фигур 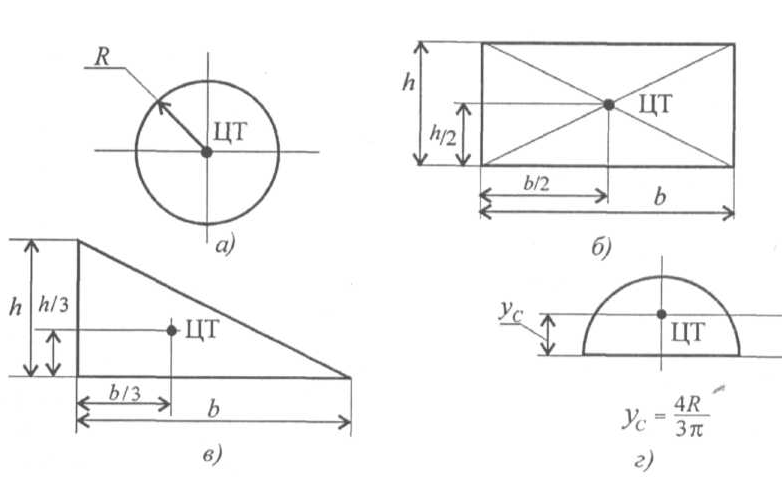 Рисунок 1 Порядок выполнения работы При решении задач на определение центра тяжести однородных тел сложной формы следует придерживаться следующего порядка: 1. Выбрать метод, который наиболее применим к данной задаче (метод разбиения или метод дополнения). 2. Разбить сложное тело на простые элементы, для которых центры тяжести известны. 3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии. 4. Определить координаты центров тяжести отдельных простых тел относительно выбранных осей. 5. Используя формулы, соответствующие выбранному методу, определить искомые координаты центра тяжести заданного тела 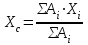 и и 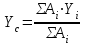 где Xcи Уc - искомые координаты центра тяжести фигуры; xiи уi— координаты центров тяжести составных частей фигуры, которые определяются из заданных размеров; Ai — площади составных частей. Пример. Вычислить координаты центра тяжести сечения сложной плоской фигуры (рис. 1,а). 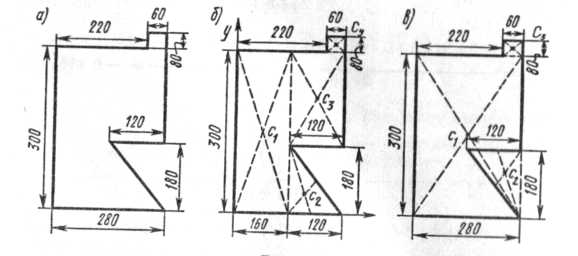 Рисунок 1 Р е ш е н и е. Заданную плоскую фигуру разбиваем на составные части, центры тяжести которых легко определяются (рис. 1, б) - прямоугольник I, треугольник II и прямоугольники III и IV. Располагаем координатные оси, как показано на рис. 6, б. Находим площади каждой части и координаты хси ус . их центров тяжести Сi. Все эти данные заносим в табл. 1 Вычисляем координаты хси усцентра тяжести плоской фигуры: 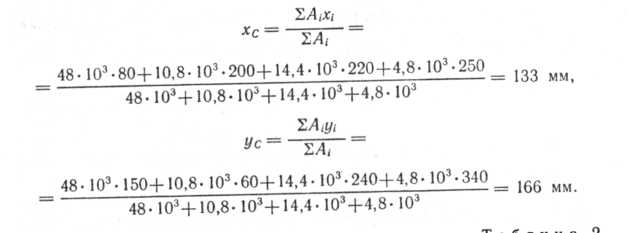 Таблица 1
При решении задач можно использовать метод отрицательных площадей, как это показано на рис. 6, в. Здесь данная фигура разделена на три части: прямоугольники I и III и треугольник II, причем площадь треугольника II, вырезанная из плоской фигуры, берется со знаком минус, т. е. считается отрицательной. Легко проверить, что если при таком разделении фигуры все исходные данные свести в табл. 3 и выполнить вычисления, то получится тот же результат. О 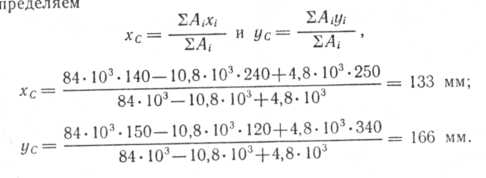 пределяем пределяемТаблица2
Центр тяжести тела в обоих случаях совпадает, что указывает на правильность решения задачи З 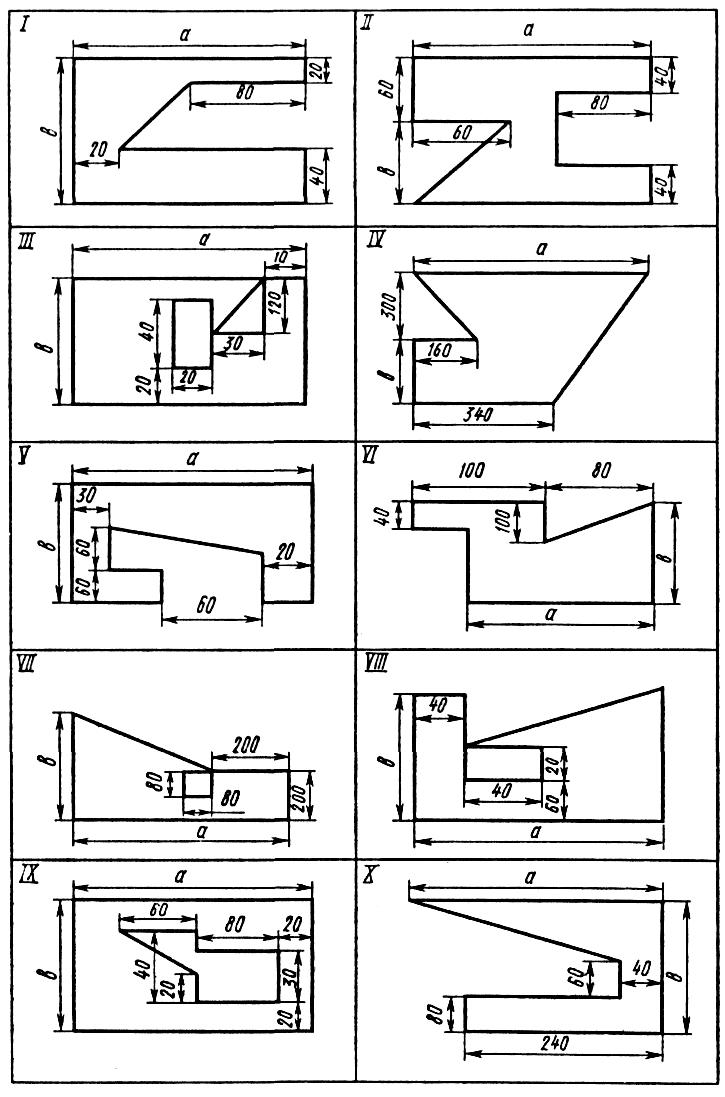 адание. Определить положение центра тяжести тонкой однородной пластинки, форма и размеры которой в миллиметрах показана на рис.1. Данные для своего варианта взять из табл.1. адание. Определить положение центра тяжести тонкой однородной пластинки, форма и размеры которой в миллиметрах показана на рис.1. Данные для своего варианта взять из табл.1.Рисунок 1Таблица 1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
