практикум твоей мамаши. Практическая работа Саморегуляция. Практическая работа 1 Модель Две популяции Для выполнения работы откройте файлзаготовку ДвеПопуляции xls
 Скачать 257.52 Kb.
|
Практическая работа №1Модель «Две популяции»Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls. Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид: 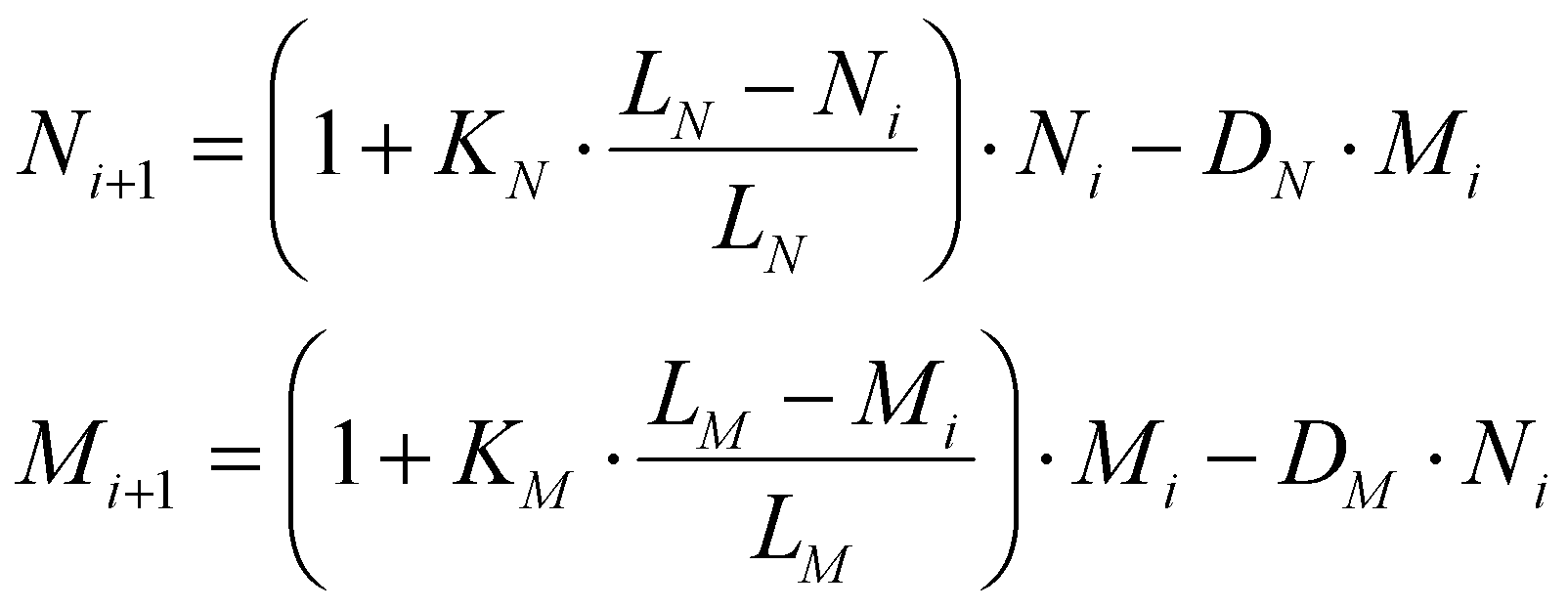 Здесь  и  – численность белок и бурундуков;  и  – их максимальные численности;  и  – коэффициенты прироста;  и  – коэффициенты взаимного влияния. Объясните, на основании каких предположений была построена эта модель. Ответ: Выполните моделирование изменения численности двух популяций в течение 15 периодов при  ,  ,  ,  ,  и  . Постройте графики изменения численности обеих популяций на одном поле. Ответьте на следующие вопросы: Является ли эта модель системной? Почему? Ответ: нет,потому что она представляет собой определенные задачи и цели,а в данной модели это не отслеживается Какова численность белок и бурундуков в состоянии равновесия? Ответ: разная,отличие составляет несколько десятков Что влияет на состояние равновесия? Ответ: окружающая среда, корм, конкуренция животных На что влияет начальная численность животных? Ответ: на количество животных в разные периоды времени При каком значении коэффициента бурундуки вымрут через 25 лет? (используйте подбор параметра).Ответ: 0,2 Найдите какие-нибудь значения коэффициентов, при которых модель становится неадекватна; Ответ: уменьшение коэффициента Предложите аналогичную модель взаимного влияния трех видов. Ответ: В вашем файле дайте письменные ответы на вопросы 1-7Прикрепите свой файл к заданию по теме «Саморегуляция»Практическая работа №2 Саморегуляция Для выполнения работы откройте файл-заготовку Саморегуляция.xls. Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности: 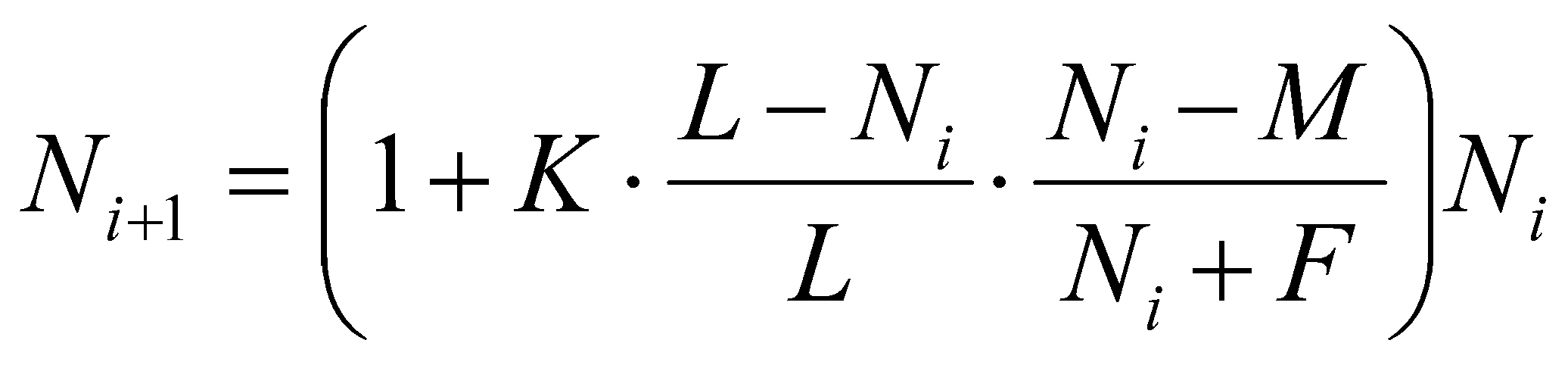 , (*)Эта модель отличатся от модели ограниченного роста только дополнительным множителем  , где и  – некоторые числа (параметры), смысл которых вам предстоит выяснить. Выполните моделирование для 30 периодов при следующих значениях параметров модели:  Сравните результаты, которые дают модель классическая модель ограниченного роста и модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей. Ответ: Постепенно увеличивая коэффициент от 0 до 500, выясните с помощью моделирования, как влияет этот коэффициент на саморегуляцию.Ответ: Через 10 периодов в результате изменения природных условия число животных уменьшилось до 400 (то есть,  ). Выполните моделирование при этих условиях и опишите, как работает саморегуляция и чем отличается поведение двух сравниваемых моделей.Ответ: Повторите моделирование п. 3 при  и сделайте аналогичные выводы:Ответ: Экспериментируя с моделями, найдите минимальную численность популяции  , при которой она выживает в соответствии с моделью (*). Ответ: Сделайте выводы о смысле коэффициента в модели (*).Ответ: Сравните свойства саморегуляции для модели ограниченного роста и модели (*). Ответ: В вашем файле дайте письменные ответы на вопросы 1-7Прикрепите свой файл к заданию по теме «Саморегуляция» |