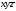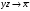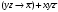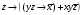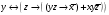Практическая работа 2. Ход работы. Задана формула f y z (y z x) x y z
 Скачать 140.28 Kb. Скачать 140.28 Kb.
|
|
Практическая работа №2. Ход работы. Задана формула: F = y ∼ z → (y z → x̅) ∨ x y z̄ =  Расставим скобки в заданной формуле Есть общепринятый порядок выполнения операций при вычислении значений произвольной формулы на каком-либо наборе аргументов. Операции выполняются в следующем порядке: 1) отрицание; 2) конъюнкция; 3) дизюнкция; 4) импликация; 5) эквиваленция и суммирование по модулю 2. Скобки могут менять порядок исполнения операций, но часто их ставят просто для удобства чтения формул. В данном случае скобки меняют порядок исполнения операций. Расставим остальные скобки в соответствии с обычным порядком исполнения, то есть просто для удобства чтения формулы: 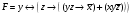 . . В дальнейшем будем пользоваться записью:  , то есть мы будем пользоваться этой последней формулой, имея в виду, что вначале исполняется операция отрицания, затем операция конъюнкции, затем операции в соответствии с расставленными скобками. , то есть мы будем пользоваться этой последней формулой, имея в виду, что вначале исполняется операция отрицания, затем операция конъюнкции, затем операции в соответствии с расставленными скобками. Составляем таблицу истинности формулы
Для операции №1 (отрицание) не выделено отдельных столбцов, чтобы не загромождать таблицу. По таблице истинности формулы 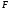 строим её матрицу Грея, отмечая наборы, на которых строим её матрицу Грея, отмечая наборы, на которых 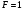 . . 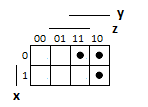 Получим ДНФ формулы 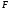 разложением по переменным. разложением по переменным. Имеем формулу 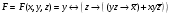 Раскладываем 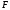 по переменной по переменной 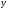 , т. к. она встречается в формуле чаще других: , т. к. она встречается в формуле чаще других: 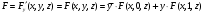 Подсчитываем 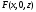 и и 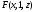 . .  ; ; 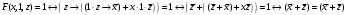 При подсчёте функции 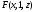 мы воспользовались свойством эквивалентности: мы воспользовались свойством эквивалентности:  для любой формулы для любой формулы 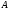 . . Теперь записываем: 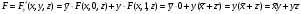 . . Получили: 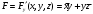 . . Раскладываем 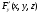 по переменной по переменной  (но можно и по переменной (но можно и по переменной  ). ). 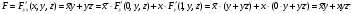 Получили: 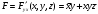 Раскладываем 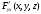 по переменной по переменной  . . 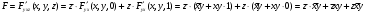 Получили: 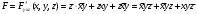 Получили СДНФ функции  . .Строим матрицу Грэя*. 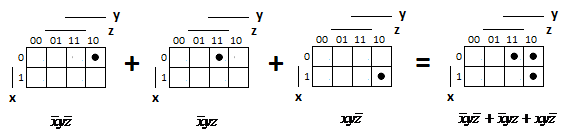 *Знаки «+» на рисунке обозначают дизъюнкцию соответствующих конъюнкций и совмещение матриц Грея этих конъюнкций. Мы могли прекратить разложение функции 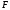 после разложения по переменной после разложения по переменной 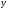 , т.к. после этого разложения мы уже получили сокращённую ДНФ функции , т.к. после этого разложения мы уже получили сокращённую ДНФ функции 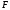 . . Получим ДНФ подстановкой кратчайших ДНФ элементарных функций, входящих в формулу 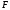 . . Имеем: 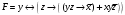 . . Сначала заменяем импликацию, используя тождество 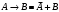 , где , где 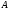 и и  любые формулы, затем сужаем область действия отрицаний. Затем приводим в скобке подобные. любые формулы, затем сужаем область действия отрицаний. Затем приводим в скобке подобные. Получаем: 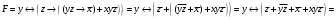 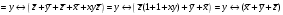 Записываем формулу  кратчайшей ДНФ: кратчайшей ДНФ: 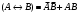 . . Получаем: 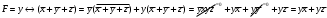 . . Получили ДНФ функции 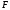 : :  . . Строим матрицу Грея. 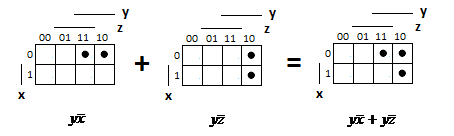 Построим сокращённую ДНФ по матрице Грея. Под сокращённой ДНФ обычно понимают ДНФ, в которой нет склеек и поглощений. Выбираем интервалы, которые покрывают все клетки матрицы Грея, на которых 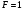 Матрицу Грея берём из пункта 2). 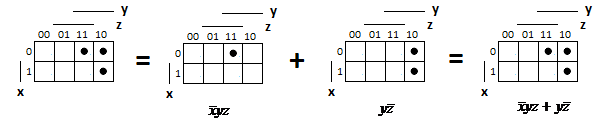 Получили сокращённую ДНФ: 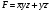 . . Перейдём от сокращённой ДНФ к совершенной ДНФ (СДНФ). Для этого домножаем конъюнкции, всходящие в сокращённую ДНФ, на единичные множители вида 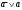 , где , где  литерал, которого нет в данной конъюнкции, раскрываем скобки, приводим подобные. литерал, которого нет в данной конъюнкции, раскрываем скобки, приводим подобные. Получаем совершенную ДНФ (СДНФ): 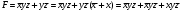 СДНФ мы уже получили ранее в пункте 3). Полученные в пунктах 3) и 5) СДНФ совпадают с точностью до порядка слагаемых и сомножителей. Поэтому матрицу Грея для полученной СДНФ мы в этом пункте можем не строить. Найдём минимальную ДНФ функции 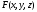 с помощью матрицы Грея. с помощью матрицы Грея. Имеем матрицу Грея (пункт 2)).  Объединяем соседние ячейки, содержащие единицы, в области Si. Соседними ячейками в диаграмме являются ячейки, двоичные номера которых различаются в одном разряде. При этом соблюдаем следующие правила. 1. Область должна быть прямоугольной. 2. Область должна содержать 2k ячеек, где k=0, 1, 2, … . 3. Область должна быть как можно больше. 4. Областей должно быть как можно меньше. 5. Области могут перекрываться. 6. Области в сумме должны покрывать все единицы. 7. Покрытие единиц областями не обязательно является однозначным. Прим. На данной карте Карно соседними являются также ячейки правого и левого столбцов. Получаем 2 области. 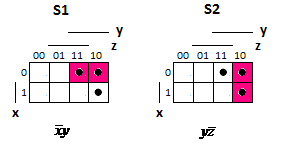 Записываем конъюнкции переменных или их отрицаний, соответствующих выделенным областям. Переменная, меняющая своё значение в выделенной области, в конъюнкцию не включается. Если переменная в выделенной области равна единице, она входит в конъюнкцию без отрицания. Если переменная в выделенной области равна нулю, она входит в конъюнкция с отрицанием. 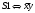 ; ; 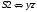 . . Объединяем конъюнкции дизъюнкцией и получаем минимальную ДНФ: 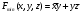 . . Получим СДНФ из минимальной ДНФ. 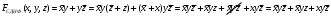 Получили:  . . Ранее в пунктах 3) и 5) мы уже получали СДНФ заданной функции 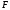 . . Мы видим, что полученная в этом пункте СДНФ совпадает с точностью до порядка слагаемых и сомножителей с СДНФ полученными в пунктах 3) и 5) . Поэтому матрицу Грея в этом пункте мы можем не строить. Все полученные в процессе решения матрицы Грея совпали. Можно сделать вывод, что решение правильное. |