!! 2022 Лаб раб метод хорд и кас. Практическая работа 3 Методы хорд и касательных

• Название: Практическая работа 3 Методы хорд и касательных
• Дата: 07.02.2023
• Размер: 84.04 Kb.
• Имя файла: !! 2022 Лаб раб метод хорд и кас.docx
• Тип: Практическая работа; #924921

Практическая работа 3

«Методы хорд и касательных»

Метод хорд.Теория

Для реализации данного метода, нужно построить исходную функцию y=F(x) и найти значения функции на концах отрезка F(a) и F(b). Затем провести хорду М₁M₂c концами в точках М₁(a, F(a)) и M₂(b, F(b)). Абсцисса точки пересечения хорды М₁M₂с осью OX это и есть приближенный корень x₁. Далее найти точку M₃(X₁ ,F(x₁ )), построить следующую хорду и найти второй приближенный корень x₂. И так далее. В зависимости от поведения функции возможны два случая:

Рис. 1

Рис. 2

Для первого случая (Рис. 1) справедлива следующая формула (8):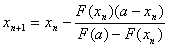



и справедливо неравенство: F(a)*F''(a)>0, где x₀=b.

Для второго случая (Рис. 2) справедлива следующая формула (9):



и справедливо неравенство: F(b)*F''(b)>0, где x₀=a.

Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона, т. е."[1]

.

Практическая часть:

Пусть дана задача следующего характера: Уточнить корни уравнения cos(2x)+x-5=0 методом хорд с точностью до 0,00001.

Для того чтобы уточнить корни уравнения cos(2x)+x-5=0 методом хорд, используя Excel, необходимо выполнить следующие действия:

1. 
   Выбрать одну из двух предложенных формул для решения задачи, для этого:
   

Найти производную первого порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f1(x)=-2sin(2x)+1.

Найти производную второго порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f2(x)=-4cos(2x).

Заполнить ячейки следующим образом:

• 
  - В ячейку A1 ввести a.
  
• 
  - В ячейку A2 ввести цифру 5.
  
• 
  - В ячейку B1 ввести b.
  
• 
  - В ячейку B2 ввести цифру 6.
  
• 
  - В ячейку C1 ввести f(x)=cos(2x)+x-5.
  
• 
  - В ячейку C2 ввести формулу =COS(2*A2)+A2-5.
  
• 
  - В ячейку D1 ввести f1(x)=-2sin(2x)+1.
  
• 
  - В ячейку E1 ввести f2(x)=-4cos(2x).
  
• 
  - В ячейку E2 ввести формулу =-4*COS(2*A2).
  
• 
  - В ячейку F1 ввести Выбор формулы.
  
• 
  - В ячейку F2 ввести формулу =ЕСЛИ(C2*E2>0;"Воспользоваться формулой 8";"Воспользоваться формулой 9").
  
• 
  - В ячейку G1 ввести e.
  
• 
  - В ячейку G2 ввести цифру 0,00001.
  

• 
  В итоге получается следующее:
  

2. 
   Исходя из того, что выбрана формула 9, в Excel необходимо выполнить следующие действия:
   

• 
  В ячейку A4 ввести xn.
  
• 
  В ячейку B4 ввести f(xn).
  
• 
  В ячейку C4 ввести b-xn.
  
• 
  В ячейку D4 ввести f(xn)*(b-xn).
  
• 
  В ячейку E4 ввести f(b).
  
• 
  В ячейку F4 ввести f(b)-f(xn).
  
• 
  В ячейку G4 ввести xn-f(xn)*(b-xn)/f(b)-f(xn).
  
• 
  В ячейку H4 ввести |f(xn)|<=e.
  
• 
  В ячейку A5 ввести цифру 5.
  
• 
  В ячейку B5 ввести формулу =COS(2*A5)+A5-5.
  
• 
  В ячейку C5 ввести формулу =$B$2-A5.
  
• 
  В ячейку D5 ввести формулу =B5*C5.
  
• 
  В ячейку E5 ввести формулу =COS(2*$B$2)+$B$2-5.
  
• 
  В ячейку F5 ввести формулу =$E$5-B5.
  
• 
  В ячейку G5 ввести формулу =A5-(B5*C5/F5).
  
• 
  В ячейку H5 ввести формулу =ЕСЛИ(ABS(B5)<=$G$2;A5;"-").
  
• 
  В ячейку A6 ввести формулу =G5.
  
• 
  Выделить диапазон ячеек B5:D5 и скопировать его методом протягивания в диапазон ячеек B6:D6.
  
• 
  Выделить диапазон ячеек F5:H5 и скопировать его методом протягивания в диапазон ячеек F6:H6.
  
• 
  Выделить диапазон ячеек A6:H6 и скопировать его методом протягивания в диапазон ячеек ниже до получения результата в одной из ячеек столбца H (A6:H9).
  

В итоге получаем следующее:



Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32976.

Метод касательных (Ньютона).Теория

В отличие от метода хорд, в методе касательных вместо хорды на каждом шаге проводится касательная к кривой y=F(x) при x=x_nи ищется точка пересечения касательной с осью абсцисс:



Формула для (n+1) приближения имеет вид:



Если F(a)*F"(a)>0, x₀=a, в противном случае x₀=b.

Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что:

.

Практическая часть

Пусть дана задача следующего характера: Уточнить корни уравнения cos(2x)+x-5=0 методом касательных с точностью до 0,00001.

Для решения такой задачи, используя Excel, необходимо выполнить следующие действия:

Изначально необходимо определиться с тем, чему равно x0: либо a, либо b. Для этого необходимо выполнить следующие действия:

Найти производную первого порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f1(x)=-2sin(2x)+1.

Найти производную второго порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f2(x)=-4cos(2x).

Заполнить ячейки следующим образом (обратить внимание на названия и номера столбцов при заполнении - они должны быть такими же, как на рисунке):



В итоге получается следующее:



Так как x0=b, то необходимо выполнить следующие действия:

Заполнить ячейки следующим образом (обратить внимание на названия и номера столбцов при заполнении - они должны быть такими же, как на рисунке):



В ячейку A6 ввести формулу =D5.

Выделить диапазон ячеек B5:E5 и методом протягивания заполнить диапазон ячеек B6:E6.

Выделить диапазон ячеек A6:E5 и методом протягивания заполнить диапазон нижерасположенных ячеек до получения в одной из ячеек столбца E результата (диапазон ячеек A6:E9).

В итоге получаем следующее:



Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32976.

Комбинированный метод хорд и касательных.Теория

Для того чтобы достичь наиболее точной погрешности, нужно одновременно использовать методы хорд и касательных. "По формуле хорд находят x_n+1 , а по формуле касательных - z_n+1 . Процесс нахождения приближенного корня прекращается, как только:



В качестве приближенного корня берут значение, равное (11):"[2]



Практическая часть:

Пусть требуется уточнить корни уравнения cos(2x)+x-5=0 комбинированным методом с точностью до 0,00001.

Для решения такой задачи, используя Excel, необходимо выполнить следующие действия:

1. 
   Так как в комбинированном методе необходимо использовать одну из формул хорд и формулу касательных, то для упрощения следует ввести следующие обозначения:
   

• 
  Для формул хорд обозначить:
  

- xn как mn.

- Переменная c будет играть роль a или b в зависимости от ситуации.

- Остальные обозначения аналогичны приведенным в формулах хорд, только учитывая выше введенные переменные.

• 
  Для формулы касательных обозначить:
  

- xn как nn.

- Остальные обозначения аналогичны приведенным в формуле касательных, только учитывая выше введенные переменные.

2. 
   Найти производную первого порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f1(x)=-2sin(2x)+1.
   
3. 
   Найти производную второго порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f2(x)=-4cos(2x).
   
4. 
   Заполнить ячейки следующим образом (обратить внимание на названия и номера столбцов при заполнении - они должны быть такими же, как на рисунке):
   

5. 
   В итоге получается следующее:
   

6. 
   В ячейку G1 ввести e, а в G2 ввести число 0,00001.
   
7. 
   В ячейку H1 ввести c, а в H2 ввести число 6, так как c=b (см. ячейку F2).
   
8. 
   В ячейку I1 ввести f(c), а в I2 ввести формулу =COS(2*H2)+H2-5.
   
9. 
   Заполнить ячейки последовательно следующим образом (обратить внимание на названия и номера столбцов при заполнении - они должны быть такими же, как на рисунке):
   

10. 
    В ячейку A6 ввести формулу =E5.
    
11. 
    В ячейку F6 ввести формулу =I5.
    
12. 
    Выделить диапазон ячеек B5:E5 и маркером автозаполнения заполнить диапазон ячеек B6:E6.
    
13. 
    Выделить диапазон ячеек G5:K5 и маркером автозаполнения заполнить диапазон ячеек G6:K6.
    
14. 
    Выделить диапазон ячеек A6:K6 и методом протягивания заполнить все нижестоящие ячейки до получения ответа в одной из ячеек столбца K (диапазон ячеек A6:K9).
    

В итоге получаем следующее: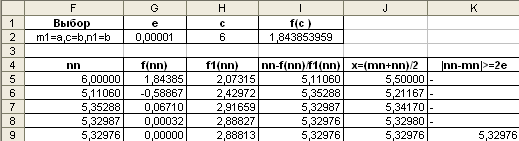





Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32976.