Главная страница
Навигация по странице:

  • «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

  • ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИИ

  • Гравитационный метод

  • Метод калькуляции затрат

    		•

    МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ. Практических заданий по дисциплине методы принятия управленческих решении


    Скачать 38.38 Kb.
    НазваниеПрактических заданий по дисциплине методы принятия управленческих решении
    Дата23.03.2022
    Размер38.38 Kb.
    Формат файлаdocx
    Имя файлаМЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ.docx
    ТипДокументы
    #410562

    Автономная некоммерческая организация высшего образования

    «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

    Кафедра экономики и управления
    Форма обучения: заочная/очно-заочная



    ВЫПОЛНЕНИЕ

    ПРАКТИЧЕСКИХ ЗАДАНИЙ

    ПО ДИСЦИПЛИНЕ

    МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИИ

    Группа

    Студент

    МОСКВА 2022

    Практические задания
    Методические рекомендации.

    Для выполнения практических заданий необходимо использовать методы «Взвешивания» и «Метод размещения с учетом полных затрат».

    Метод взвешивания - учитывает факторы, важные для размещения, но которые не всегда возможно представить в числовом виде. Различие между факторами отражается в начислении баллов.

    Рекомендации

    1. Составляется список факторов, влияющих на размещение производства.

    2. Каждому фактору приписывается вес - число из отрезка (0;1). Сумма всех весов должна равняться единице.

    3. Выбирается шкала для измерения каждого фактора (например, от 1 до 10).

    4. Умножается оценка факторов на соответствующие веса и суммируются полученные числа для каждого из возможных вариантов размещения производства. Вариант с наибольшей суммой является наилучшим.

    Пример 1

    Рассматривается вопрос о строительстве поликлиники. Существуют три возможных варианта строительства А, В, С. Исходные данные отразим в таблице:

    Фактор
    Вес
    А
    В
    С

    Доступность для пациентов
    0,5
    10
    8
    7

    Арендная плата
    0,3
    5
    4
    6

    Удобство для персонала
    0,2
    3
    6
    5

    Дадим рекомендации о месте строительства, используя метод взвешивания:

    Фактор
    |Вес|
    А
    В
    С
    Вес*А
    Вес*В
    Вес*С

    Доступное ть для пациентов
    0,5
    10
    8
    7
    5
    4
    3,5

    Арендная плата
    0,3
    5
    4
    6
    1,5
    1,2
    1,8

    Удобство для персонала
    0,2
    3
    6
    5
    0,6
    1,2
    1

    Сумма
    1
    -
    -
    -
    7,1
    6,4
    6,3


    Вариант с наибольшей суммой (7,1) — это строительство поликлиники в районе А.

    Задание для самостоятельной работы

    Взять данные из таблицы и произвести расчеты по выбору варианта строительства.

    Обосновать вывод по выбору варианта в соответствии с полученными результатами.


    Вариант
    Значения показателя
    Факторы

    Доступность для пациентов
    Арендная плата
    Удобство для персонала

    1
    Вес
    0,3
    0,6
    0,1

    A
    10
    5
    3

    B
    8
    4
    6

    C
    7
    6
    5

    2
    Вес
    0,4
    0,2
    0,4

    A
    9
    1
    9

    B
    8
    3
    6

    C
    4
    1
    2

    3
    Вес
    0,2
    0,6
    0,2

    A
    7
    10
    5

    B
    1
    5
    9

    C
    4
    6
    8

    4
    Вес
    0,6
    0,1
    0,3

    A
    2
    5
    2

    B
    9
    3
    8

    C
    5
    5
    1


    Дополним таблицу:


    Вариант
    Значения показателя
    Факторы
    1
    2
    3
     

    Доступность для пациентов
    Арендная плата
    Удобство для персонала
    Вес*А Вес*В Вес*С
    Вес*А Вес*В Вес*С
    Вес*А Вес*В Вес*С
    Сумма

    1
    Вес
    0,3
    0,6
    0,1
     
     
     
    1 

    A
    10
    5
    3
    3
    3
    0,3
    6,3

    B
    8
    4
    6
    2,4
    2,4
    0,6
    5,4

    C
    7
    6
    5
    2,1
    3,6
    0,5
    6,2

    2
    Вес
    0,4
    0,2
    0,4
     
     
     
     

    A
    9
    1
    9
    3,6
    0,2
    3,6
    7,4

    B
    8
    3
    6
    3,2
    0,6
    2,4
    6,2

    C
    4
    1
    2
    1,6
    0,2
    0,8
    2,6

    3
    Вес
    0,2
    0,6
    0,2
     
     
     
     

    A
    7
    10
    5
    1,4
    6
    1
    8,4

    B
    1
    5
    9
    0,2
    3
    1,8
    5

    C
    4
    6
    8
    0,8
    3,6
    1,6
    6

    4
    Вес
    0,6
    0,1
    0,3
     
     
     
     

    A
    2
    5
    2
    1,2
    0,5
    0,6
    2,3

    B
    9
    3
    8
    5,4
    0,3
    2,4
    8,1

    C
    5
    5
    1
    3
    0,5
    0,3
    3,8



    Произведем расчеты.

    Вариант 1:

    А = 0,3 * 10 +0,6 * 5 + 0,1 * 3 = 6,3

    В = 0,3 * 8 + 0,6 * 4 + 0,1 * 6 = 5,4

    С = 0,3 * 7 + 0,6 * 6 + 0,1 * 5 = 6,2

    При выборе варианта строительства поликлиники по 1 варианту наилучшим является вариант А, т.к. его вес в данном случае с наибольшей суммой (6,3).
    Вариант 2:

    А = 0,4 * 9 +0,2 * 1 + 0,4 * 9 = 7,4

    В = 0,4 * 8 +0,2 * 3 + 0,4 * 6 = 6,2

    С = 0,4 * 4 +0,2 * 1 + 0,4 * 2 = 2,6

    При выборе варианта строительства поликлиники по 2 варианту наилучшим является вариант А, т.к. его вес в данном случае с наибольшей суммой (7,4).
    Вариант 3:

    А = 0,2 * 7 +0,6 * 10 + 0,2 * 5 = 8,4

    В = 0,2 * 1 +0,6 * 5 + 0,2 * 9 = 5,0

    С = 0,2 * 4 +0,6 * 6 + 0,2 * 8 = 6,0
    При выборе варианта строительства поликлиники по 3 варианту наилучшим является вариант А, т.к. его вес в данном случае с наибольшей суммой (8,4).
    Вариант 4:

    А = 0,6 * 2 +0,1 * 5 + 0,3 * 2 = 2,3

    В = 0,6 * 9 +0,1 * 3 + 0,3 * 8 = 8,1

    С = 0,6 * 5 +0,1 * 5 + 0,3 * 1 = 3,8
    При выборе варианта строительства поликлиники по 4 варианту наилучшим является вариант В, т.к. его вес в данном случае с наибольшей суммой (8,1).
    Метод размещения с учетом полных затрат

    Данный метод основан на анализе затрат и объемов выпуска. Для каждого варианта определяются постоянные и переменные затраты. Выбирается вариант размещения с наименьшими совокупными затратами для определенного объема производства.

    Пример 2

    Рассматривается вопрос о строительстве завода в одном из трех городов: А, В, С. Исследование показало, что постоянные затраты (за год) в этих городах равны 20000, 50000 и 80000 рублей соответственно, а переменные затраты - 65, 45 и 30 рублей за единицу продукции соответственно. Ожидаемый годовой объем выпуска -5000 единиц. Определим место строительства с учетом полных затрат.

    Решение

    20000 +65 * 5000 =345000 рублей / год (А)

    50000 + 45 * 5000 = 275000 рублей /год(В)

    80000 + 30 * 5000 = 230000рублей / год(С)

    Наилучший вариант — это город С, так как там минимум совокупные затраты при ожидаемом годовом объеме выпуска 5000 единиц.

    Задание для самостоятельной работы

    Провести расчеты для каждого варианта задания и объяснить выбор по результатам расчета.

    Вариант 1

    Рассматривается вопрос о строительстве завода в одном из трех городов: А, В, С. Исследование показало, что постоянные затраты (за год) в этих городах равны 25000, 45000 и 70000 рублей соответственно, а переменные затраты - 55, 40 и 35 рублей за единицу продукции соответственно. Ожидаемый годовой объем выпуска - 8000 единиц. Определим место строительства с учетом полных затрат.

    Решение:

    25000 + 55 * 8000 = 465000 рублей / год (А)

    45000 + 40 * 8000 = 365000 рублей /год (В)

    70000 + 35 * 8000 = 350000 рублей / год (С)

    Наилучший вариант — это город С, так как там минимум совокупные затраты при ожидаемом годовом объеме выпуска 8000 единиц.

    Разумеется, при принятии решений эти данные следует рассматривать только в качестве стартовых. Предприятие должно провести более подробный анализ затрат, долгосрочных планов, своих целей и рассмотреть другие значимые факторы.

    Вариант 2

    Рассматривается вопрос о строительстве завода в одном из трех городов: А, В, С. Исследование показало, что постоянные затраты (за год) в этих городах равны 16866, 20726 и 48709 рублей соответственно, а переменные затраты - 22, 87 и 28 рублей за единицу продукции соответственно. Ожидаемый годовой объем выпуска - 5000 единиц. Определим место строительства с учетом полных затрат.

    Решение:

    16866 + 22 * 5000 = 126866 рублей / год (А)

    20726 + 87 * 5000 = 455726 рублей /год (В)

    48709 + 28 * 5000 = 188709 рублей / год (С)

    Наилучший вариант — это город А, так как там минимум совокупные затраты при ожидаемом годовом объеме выпуска 5000 единиц.

    Вариант 3

    Рассматривается вопрос о строительстве завода в одном из трех городов: А, В, С. Исследование показало, что постоянные затраты (за год) в этих городах равны 32948, 80142 и 36293 рублей соответственно, а переменные затраты - 88, 18 и 99 рублей за единицу продукции соответственно. Ожидаемый годовой объем выпуска - 4000 единиц. Определим место строительства с учетом полных затрат.

    Решение:

    32948 + 88 * 4000 = 384948 рублей / год (А)

    80142 + 18 * 4000 = 152142 рублей /год (В)

    36293 + 99 * 4000 = 432293 рублей / год (С)

    Наилучший вариант — это город В, так как там минимум совокупные затраты при ожидаемом годовом объеме выпуска 4000 единиц.

    Вариант 4

    Рассматривается вопрос о строительстве завода в одном из трех городов: А, В, С. Исследование показало, что постоянные затраты (за год) в этих городах равны 31257, 65500 и 74595 рублей соответственно, а переменные затраты - 20, 1 и 78 рублей за единицу продукции соответственно. Ожидаемый годовой объем выпуска - 9000 единиц. Определим место строительства с учетом полных затрат.

    Решение:

    31257 + 20 * 9000 = 211257 рублей / год (А)

    65500 + 1 * 9000 = 74500 рублей /год (В)

    74595 + 78 * 9000 = 776595 рублей / год (С)

    Наилучший вариант — это город В, так как там минимум совокупные затраты при ожидаемом годовом объеме выпуска 9000 единиц.
    Гравитационный метод

    Данный метод служит для размещения объектов производства (инфраструктуры) в зависимости от связанных с ним других объектов (например размещение магазина относительно жилых домов).

    Пусть (xi , yi ) – координаты i-го магазина, wi – объем поставляемой в i-й магазин продукции (I = 1,…, n). Тогда торговый дом необходимо разместить в центре гравитации – точке с координатами (Cx , Сy ), где: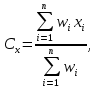

    Пример 1

    Предполагается создать центральный узел связи для обслуживания почтовых отделений A, B, C, D.

    Фактор
    Координаты
    Число поездок почтового фургона в день

    A
    (9;6)
    3

    B
    (7;8)
    4

    C
    (1;5)
    5

    D
    (2;10)
    2


    Определить координаты центра гравитации для размещения узла связи.

    Определим координаты центра гравитации для размещения центрального узла связи.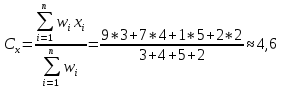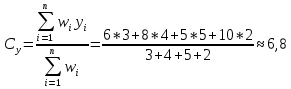





    Ответ: (4,6;6,8)

    Задание для самостоятельной работы

    Предполагается создать центральный узел связи для обслуживания почтовых отделений A, B, C, D.

    Фактор
    Координаты
    Число поездок почтового фургона в день

    A
    (7;9)
    3

    B
    (10;4)
    1

    C
    (2;5)
    2

    D
    (8;6)
    4


    Определить координаты центра гравитации для размещения узла связи.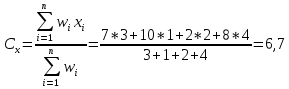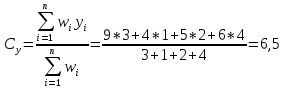





    Ответ: Координаты центра гравитации для размещения центрального узла связи равны: Сх = 6,7, Cy = 6,5.
    Метод калькуляции затрат

    Данный метод принимает во внимание только затраты на перевозку. Этот метод служит, например, для выбора единственного торгового дома, обслуживающего несколько магазинов m возможных вариантов.

    Пусть (xi, yi) – координаты i-го магазина, wi – число ежедневных поставок в i-й магазин продукции (I = 1,…, n), (xj0, yj0) – координаты j-го возможного расположения торгового дома (j=1,.., m).

    Предпочтение отдается тому j-му возможному варианту, для которого сумма: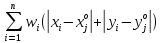



    будет минимальной.

    Пример 2

    Изменим данные прошлого примера: выберем расположение центрального узла связи из двух возможных вариантов: (6; 8) и (4; 7). Заполняем таблицы для варианта (6; 8).


    Почтовое отделение
    xi
    yi
    Wi

    A
    9
    6
    3

    B
    7
    8
    4

    C
    1
    5
    5

    D
    2
    10
    2


    Заполним таблицу для варианта (6, 8).

    Почтовое отделение
    |xi -6|
    |yi-8|
    |xi -6|+|yi-8|
    Wi*(|xi -6|+|yi-8|)

    A
    3
    2
    5
    15

    B
    1
    0
    1
    4

    C
    5
    3
    8
    40

    D
    4
    2
    6
    12

    Сумма









    71


    Аналогично заполняем таблицу для возможного варианта (4;7)


    Почтовое отделение
    |xi -4|
    |yi-7|
    |xi -4|+|yi-7|
    Wi*(|xi -4|+|yi-7|)

    A
    5
    1
    6
    18

    B
    3
    1
    4
    16

    C
    3
    2
    5
    25

    D
    2
    3
    5
    10

    Сумма









    69


    Так как 69 <71, то наилучший вариант – это (4;7)

    Задание для самостоятельной работы

    Изменим данные прошлого примера: выберем расположение центрального узла связи из двух возможных вариантов: (5; 7) и (6; 4).

    Заполним таблицу для варианта (5;7).

    Почтовое отделение
    |xi -5|
    |yi-7|
    |xi -5|+|yi-7|
    Wi*(|xi -5|+|yi-7|)

    A
    4
    1
    5
    15

    B
    2
    1
    3
    12

    C
    4
    2
    6
    30

    D
    3
    3
    6
    12

    Сумма









    69


    Заполним таблицу для варианта (6;4).

    Почтовое отделение
    |xi -6|
    |yi-4|
    |xi -6|+|yi-4|
    Wi*(|xi -6|+|yi-4|)

    A
    3
    2
    5
    15

    B
    1
    4
    5
    20

    C
    5
    1
    6
    30

    D
    4
    6
    10
    20

    Сумма









    85


    Ответ: Предпочтение отдается тому j-му возможному варианту, для которого сумма будет минимальной. Так как 69 <85, то наилучший вариант – это (5;7).

    написать администратору сайта