фыизика. ТЕХНОЛОНИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ. Приложения определенного интеграла вычисление площади плоских фигур, длины дуги плоской кривой, вычисление объема тела
 Скачать 197.9 Kb.
|
|
Тема: Приложения определенного интеграла: вычисление площади плоских фигур, длины дуги плоской кривой, вычисление объема тела. Пусть функция непрерывна и неотрицательна на отрезке [a,b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции , может быть вычислена по формуле (см. 10.1 рис. 1). 1.2. Если на отрезке [a,b], непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций вычисляется по формуле 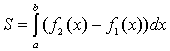 (рис. 10).1.3. Если функция на отрезке [a,b] принимает значения разных знаков, то площадь фигуры, заключенная между кривой и осью , равна (рис. 11).  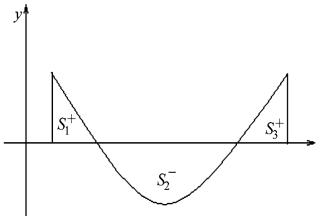 Рис. 10 Рис. 11 П р и м е р 15. Вычислить площадь фигуры, ограниченной графиками функций и . Решение. Вычислим координаты точек пересечения графиков этих функций. Для этого решим систему 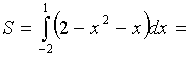 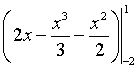 = 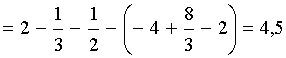кв. ед. (рис. 12).1.4. При вычислении площади криволинейной трапеции, в случае когда верхняя граница задана параметрическими уравнениями 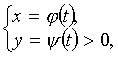 t в формуле надо сделать замену переменной, положив , тогда получим 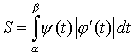 , где и значения параметра t, соответствующие значениям x=a и x=b, т. е. .П 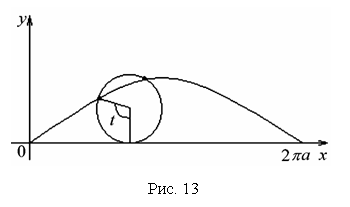 р и м е р 16. Найти пло-щадь фигуры, ограниченной одной аркой циклоиды 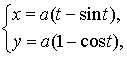 и осью .Замечание. Циклоида плоская кривая, которую описывает точка М окружности радиуса a, катящаяся без скольжения по прямой линии (рис. 13). Решение. Искомая площадь 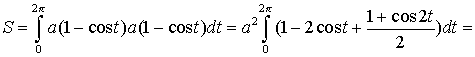 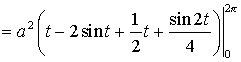 ; .П р и м е р 17. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями 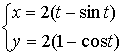 , y = 2 .Решение. Из условия задачи следует, что y>0 при любом t. Решим неравенство  , , .Но по условию . При k = 0 2 t 32 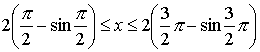 , .При x не будет принадлежать интервалу . Фактически нужно вычислить площадь фигуры, заключенной между прямой y = 2 и частью циклоиды, расположенной выше этой прямой (рис. 14). Искомая площадь 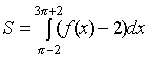 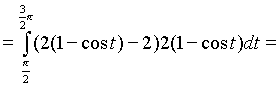 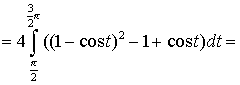  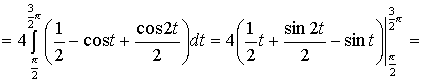 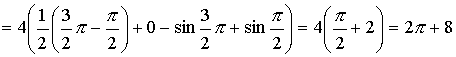 .2 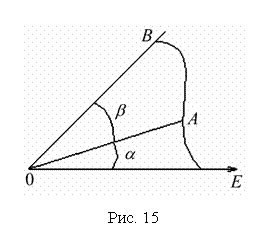 . Вычисление площади криволинейного сектора. Пусть кривая AB зада-на в полярных координатах уравнением , , причем непрерывная и неотрицательная на отрезке функция. Фигуру, ограниченную кривой AB и двумя полярными радиусами, составляющими с полярной осью углы , будем называть криволинейным сектором.Площадь криволинейного сектора может быть вычислена по формуле . (27) П р и м е р 18. Вычислить площадь фигуры, ограниченной кривой (4-лепестковая роза рис. 16). Решение. Меняя непрерывно от 0до , можно построить первый лепесток. Составим таблицу значений функций (табл. 3). Таблица 3
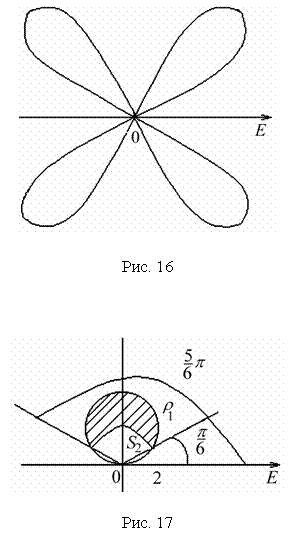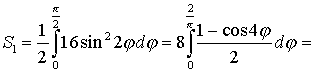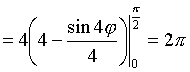В  ычислим площадь одного лепестка по формуле (27)  .Следовательно, площадь всех лепестков . П р и м е р 19. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями , (рис. 17). Решение. При изменении от 0 до полярный радиус опишет кривую, изображенную на (рис. 17), при . Уравнение есть уравнение окружности с центром в точке 0 радиуса 2. Найдем, при каких линии пересекаются. Для этого решим систему 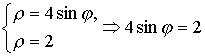 ;; ; . И тогда искомая площадь 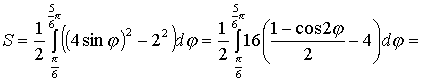 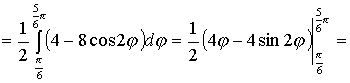 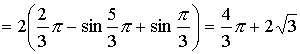 ;. 3. Вычисление длины дуги плоской кривой 3.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a,b], то длина дуги AB, где A(a,f(a)), B(b,f(b)), выражается формулой 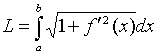 . (28)3.2. Если кривая задана параметрическими уравнениями , где x(t),y(t) дифференцируемые функции, то длина дуги 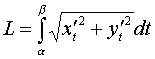 . (29)3.3. Если дуга задана в полярных координатах , , то длина дуги 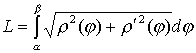 . (30)П р и м е р 20. Вычислить длины дуг плоских кривых: а) ; б) 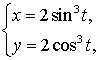 ;в) , . Решение. а) Воспользуемся формулой (10). Так как 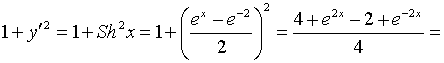 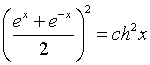 ,то 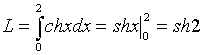 .б) Воспользуемся формулой (11). Так как , то 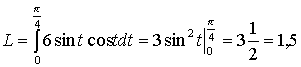 .в)  .4. Вычисление объемов. Нахождение объемов некоторых тел можно свести к вычислению определенных интегралов. 4.1. Вычисление объема тела по известным площадям параллельных сечений. Если известны площади сечений тела плоскостями, перпендикулярными оси OX, т. е., зная х, мы можем вычислить площадь сечения S = S (x). Тогда объем тела в предположении, что S(x)интегрируемая функция. 4.2. Вычисление объема тела вращения: а) если тело образовано вращением криволинейной трапеции, ограниченной кривой y = f(x), осью OX и двумя прямыми x = a иx = b(a < b) вокруг оси OX, то объем тела ; б) а если тело образовано вращением фигуры, ограниченной кривой , прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем ; в) если тело образовано вращением вокруг оси OY фигуры, ограниченной линией y = f (x), прямыми x = a,x = b и осью OX, то его объем можно вычислить по формуле ; г) если вращается вокруг полярной оси криволинейный сектор, ограниченный дугой , двумя полярными радиусами и , то объем полученного тела может быть вычислен по формуле 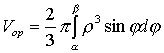 .П р и м е р 21. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций и вокруг оси OX. Решение. Найдем точки пересечения параболы и прямой . Решим систему: Получим две точки пересечения: х 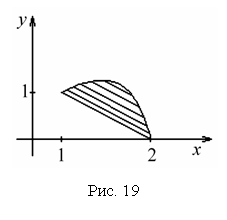 1 = 1, у1 = 1; х2 = 2, у2 = 0.Сделаем чертеж (рис. 19).     .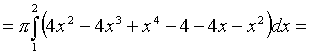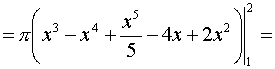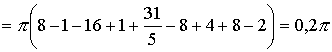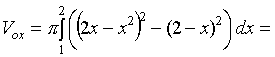
; z = 0; z = 3. Решение. однополостной гиперболоид. При пересечении его плоскостями z = h в сечении получаем эллип-сы (рис. 20) с полуосями , . Как известно, площадь эллипса 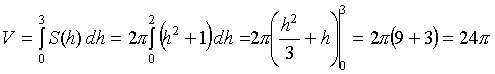 куб. ед.5. Вычисление площади поверхности вращения 5.1. Поверхность, образованная вращением кривой , a < x < b вокруг оси OX, имеет площадь 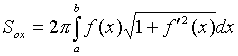 .5.2. Если кривая задана параметрическими уравнениями , причем , то  .5.3. Если дуга , , задана в полярной системе координат кривой, и вращается вокруг полярной оси, то площадь поверхности вращения можно вычислить по формуле 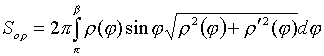 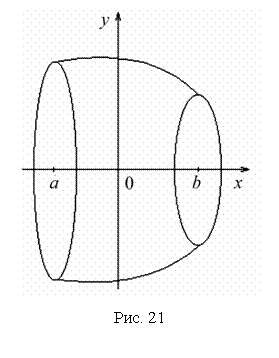 .П р и м е р 23. Найти площадь поверхности шарового пояса, образованного вращением части окружности x2 + y2= R2 вокруг оси OX (рис. 21). Решение. Из уравнения окружности имеем . Вращаем вокруг оси ОХ дугу верхней части. Найдем и Тогда по соответствующей формуле площадь шарового пояса 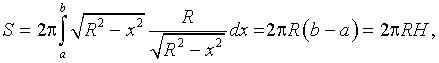 Физические приложения определенного интеграла Вычисление работы с помощью определённого интеграла. Пусть под действием некоторой силы материальная точка М движется по прямой в направлении оси . Требуется найти работу, произведённую силой при перемещении точки М из положения в положение . 1) Если сила постоянна , то работа выражается следующим образом . 2) Если сила переменная величина, то . Пример: Два электрических заряда и находятся на оси соответственно в точках и . Какая работа будет произведена, если второй заряд переместится в точку ? (Сила взаимодействия зарядов ). Решение: = 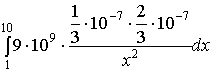 = = == . Координаты центра тяжести. Центром тяжести совокупности материальных точек называется центр параллельных сил тяжести, приложенных в этих точках. Для материальной дуги АВ плоской кривой прямоугольные координаты центра тяжести определяются формулами : 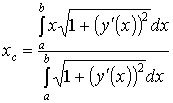 ,  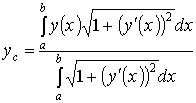.Для материальной однородной криволинейной трапеции, прилежащей к оси и имеющей верхнюю границу , центр тяжести имеет координаты где площадь криволинейной трапеции. Центр тяжести произвольной плоской, ограниченной графиком функции сверху и снизу, определяется формулами 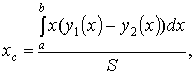 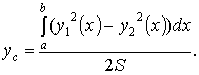 Пример: Найти координаты центра тяжести однородного полукруга , расположенного над осью . Решение: Применим формулы Так как полукруг расположен над осью , то верхняя граница задаётся уравнением В силу симметрии фигуры относительно оси ординат, абсцисса центра тяжести равна нулю. Найдём ординату: 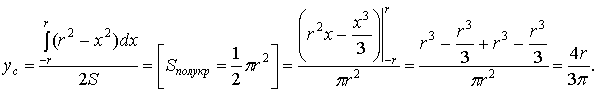 Координаты центра тяжести имеют вид |
