Корреляционное моделирование. Проект_Кореляционное_моделирование. Проект Моделирование корреляционных зависимостей
 Скачать 196.69 Kb. Скачать 196.69 Kb.
|
|
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ “ЗУГРЭССКАЯ СРЕДНЯЯ ШКОЛА №10 г. ХАРЦЫЗСКА” Проект: Моделирование корреляционных зависимостейВыполнили: Ученики 11-А класса Жартовская Дарья Киров Константин Руководитель: Учитель информатики Данилец О.Ф 2023 Содержание 1.Информационное моделирование 2.Моделирование статистического прогнозирования 3.Регрессионные математические модели 4. Функция вычисления 5.Таблицы   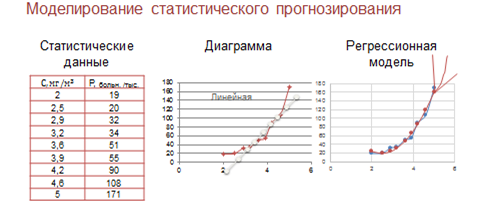 Есть два способа прогнозирования по регрессионной модели. Первый способ. Если прогноз рассчитывается в пределах экспериментальных значений независимой переменной. Такой прогноз называется восстановлением значения. Второй способ. Если прогноз рассчитывается за пределами экспериментальных данных. Такой прогноз называется экстраполяцией.  Образцовым примером такой зависимости является связь между ростом отцов и детей. Конечно, у высокого отца может быть низкорослый сын, а у низкорослого — высокий, но в большинстве случаев прослеживается склонность увеличения роста детей с увеличением роста отцов. Регрессионные математические модели строятся в тех случаях, когда известно, что зависимость между двумя факторами существует и требуется получить ее математическое описание. Давайте рассмотрим задачи другого рода. Пусть важной характеристикой некоторой сложной системы является фактор A, на него могут оказывать влияние одновременно многие другие факторы: B, C, D и так далее. Рассмотрим два типа задач: 1) Требуется, определить, оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А? 2) Какие из факторов B, C, D и так далее оказывают наибольшее влияние на фактор А? В качестве примера сложной системы рассмотрим школу. Пусть, для первого типа задач фактором А, является средняя успеваемость учащихся школы, фактором В финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п. Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие, причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и другие. Специалисты по статистике знают, что для того, чтобы выявить зависимость от какого-то определенного фактора, нужно максимально исключить влияние других факторов. Проще говоря, собирая, информацию из разных школ, нужно выбирать такие школы., в которых приблизительно одинаковый контингент учеников, квалификация учителей и пр., нехозяйственные расходы школ разные (у одних школ могут быть богатые спонсоры, у других— нет). так, пусть хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу учеников в школе (руб./чел.), потраченных за определенный период времени (например, за последние 5 лет). Успеваемость же, пусть оценивается средним баллом учеников школы по результатам окончания последнего учебного года
 Приведена точечная диаграмма, построенная по этим данным, достаточно знать следующее: коэффициент корреляции (обычно обозначаемый греческой буквой р) есть число, заключенное в диапазоне, если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая: близость ρ к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное: значение р легко найти с помощью MS Excel без всяких, формул (разумеется, потому, что в MS Excel они встроены). В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит в группу статистических функций. Как же ей воспользоваться? Установим курсор на любую свободную ячейку и запустим функцию КОРРЕЛ. Она запросит два диапазона значений. Укажем В2:В21 и С2:С21. После их ввода выведется ответ: р= 0,500273843. Эта величина говорит о среднем: уровне корреляции. Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием: ходят в чистую, красивую, уютную школу, чувствуют там себя, как дома, и поэтому лучше учатся. В следующем примере проводится исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и обеспеченности школы компьютерами. И та и другая характеристика количественно выражаются в процентах от нормы. Нормой обеспеченности учебниками является их полный комплект, то есть такое количество, когда каждому ученику выдаются из библиотеки все нужные ему для учебы: книги. Нормой обеспеченности компьютерами будем считать такое их количество, при котором на каждые четыре старшеклассника в школе приходится: один: компьютер. Предполагается, что компьютерами ученики пользуются не только на информатике, но и на других уроках, а также во внеурочное время. В таблице 2, приведены результаты измерения обоих факторов в 10 разных школах. Напомним, что влияние каждого фактора исследуется независимо от других (то есть влияние других существенных факторов должно быть приблизительно одинаковым). Значения обеих величин: финансовых затрат и успеваемости учеников имеют значительный разброс и, на первый взгляд, взаимосвязи между ними не видно. Однако она вполне может существовать. Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционнными зависимостями. Раздел математической статистики, который исследует такие зависимости, называется корреляиионным анализом. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости. Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции. Как и прежде, мы не будем писать формулы, по которым он вычисляется; их написать нетрудно, гораздо труднее понять, почему они именно такие
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
