Контрольная термех. Динамика вариант 14. Расчётнографическая работа по разделу Динамика
 Скачать 489.33 Kb. Скачать 489.33 Kb.
|
|
Балтийский государственный технический университет «Военмех» им. Д.Ф. Устинова Кафедра теоретической механики и баллистики Расчётно-графическая работа №___ по разделу «Динамика» Вариант № 14 Выполнил:__________________ Группа_______ Проверил:___________________ Санкт-Петербург 20__ Задание 1 Материальная точка М движется относительно стержня АВ (цилиндрический канал АВ). Движение стержня АВ задано. Определить движение точки М относительно стержня и давление, производимое ею на стенки стержня. Данные, необходимые для решения задач, приведены в таблице, где 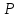 – вес точки – вес точки 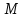 , , 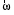 – угловая скорость (постоянная величина), – угловая скорость (постоянная величина), l – длина недеформированной пружины, 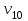 – начальная скорость точки М относительно подвижного тела (при – начальная скорость точки М относительно подвижного тела (при 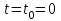 ), φ0– значение угловой координаты φ при статическом равновесии вещественной точки, ), φ0– значение угловой координаты φ при статическом равновесии вещественной точки, 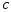 – жёсткость пружины. – жёсткость пружины.
Оси 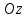 и и 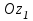 направлены перпендикулярно плоскости чертежа. направлены перпендикулярно плоскости чертежа. Переносное движение – вращение вокруг горизонтальной оси. В начальный момент времени пружина не напряжена. Ход решения Решение. Дано: 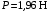 , , 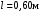 , , 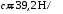 , , 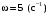 при начальных условиях: при начальных условиях: 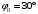 , , 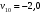 м/с. м/с. 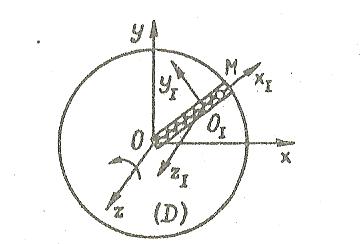 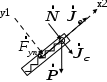 Рис. 1 Рис. 2 Система отсчёта, оси координат приведены на рис. 1, действующие силы на рис.2. Подвижную систему координат 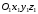 удобно жёстко связать со стержнем удобно жёстко связать со стержнем 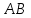 . Неподвижная система координат . Неподвижная система координат 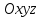 связана с осью вращения стержня. связана с осью вращения стержня.Стержень равномерно вращается вокруг неподвижной оси 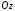 . На шарик в стержне действуют следующие силы: . На шарик в стержне действуют следующие силы:1) сила тяжести 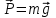 ; ; 2) сила упругости пружины 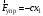 ( (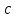 – коэффициент пропорциональности); – коэффициент пропорциональности); 3) реакция трубки 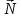 , имеющая составляющую , имеющая составляющую 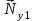 (предполагаем отсутствие силы трения в трубке, поэтому (предполагаем отсутствие силы трения в трубке, поэтому 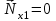 , все силы приложены в плоскости вращения и , все силы приложены в плоскости вращения и 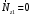 ). ). Для определения давления материальной точки на стенки стержня необходимо найти силу реакции стержня: 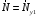 . .Трубка вращается равномерно, поэтому переносное ускорение имеет только осестремительную составляющую 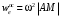 . . Переносная сила инерции направлена от оси вращения и её модуль равен 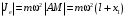 . .Кориолисова сила инерции 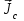 направлена противоположно оси направлена противоположно оси 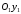 , ,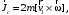 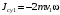 . .С учетом всех названных сил, согласно основному уравнению динамики в подвижной системе координат 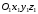 имеем имеем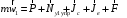 . (1) . (1)В проекциях на оси подвижной системы координат 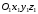 имеем систему уравнений имеем систему уравнений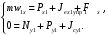 (2) (2)Учитывая, что 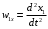 и следовательно и следовательно 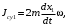 получаем систему из трех уравнений получаем систему из трех уравнений 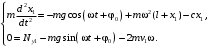 (3) (3)Первое уравнение равносильно: 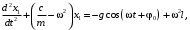 (4) (4)Численное значение 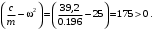 Если обозначить 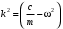 , тогда , тогда 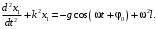 (5) (5)Мы получили неоднородное дифференциальное уравнение второго порядка. Решение складывается из общего решения однород- ного уравнения х11 и частного решения неоднородного уравнения х12: х1 =х11 + х12. Найдём общее решение однородного уравнения. Характеристическое уравнение имеет вид 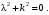 Его корни мнимые, поэтому общее решение однородного уравнения имеет вид Его корни мнимые, поэтому общее решение однородного уравнения имеет вид 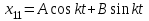 . (6) . (6)Для нахождения частного решения дифференциальногом уравнения, обусловленного членом – 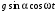 , будем использовать метод Лагранжа (метод вариации произвольных постоянных). Заменим произвольные постоянные в общем решении на функции , будем использовать метод Лагранжа (метод вариации произвольных постоянных). Заменим произвольные постоянные в общем решении на функции 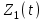 и и 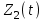 . Учитывая (5) и (6), составим систему уравнений для нахождения решения: . Учитывая (5) и (6), составим систему уравнений для нахождения решения: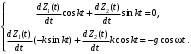 (7) (7)Решим эту систему уравнений методом Крамера: 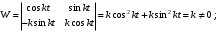 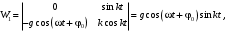 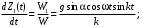 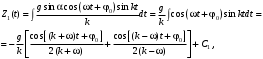 где С1– постоянная интегрирования; 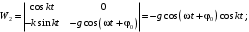 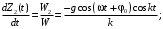 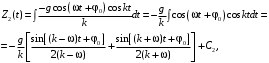 где где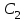 – постоянная интегрирования; – постоянная интегрирования;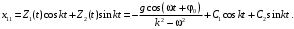 Далее частное решение, обусловленное постоянным членом 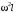 ищем в виде ищем в виде 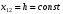 , поэтому , поэтому 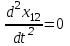 , следовательно, , следовательно, 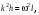 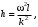 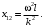 Таким образом, решение для х1 имеет вид 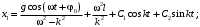 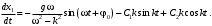 Подставив начальные условия 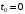 , , 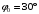 , , 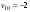 м/с в полученные уравнения, находим постоянные интегрирования С1 и С2: м/с в полученные уравнения, находим постоянные интегрирования С1 и С2: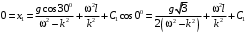 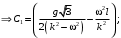 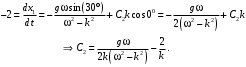 Подставив константы 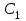 и и 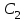 , получим уравнение относительного движения точки: , получим уравнение относительного движения точки: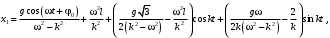 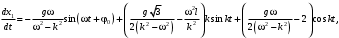 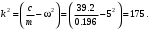 Тогда сила реакции стержня равна: 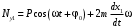 Подставив данные, получим закон движения точки в неинерциальной системе отсчёта 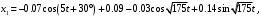 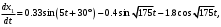 Получаем величину силы реакции трубки 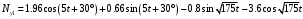 Задание 3 В 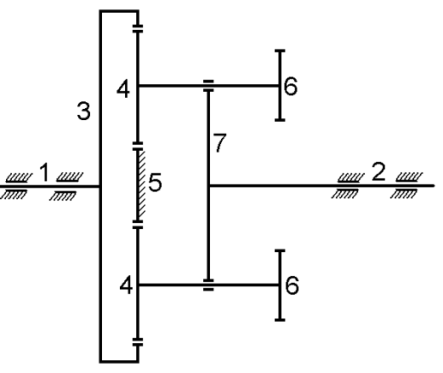 соответствии с выданным вариантом задания привести схему грузовой лебедки и поднимаемого груза по наклонной плоскости (см. рис. 3.6 и 3.7, табл. 3.1 и 3.2). соответствии с выданным вариантом задания привести схему грузовой лебедки и поднимаемого груза по наклонной плоскости (см. рис. 3.6 и 3.7, табл. 3.1 и 3.2).Рис.3 Схема редуктора 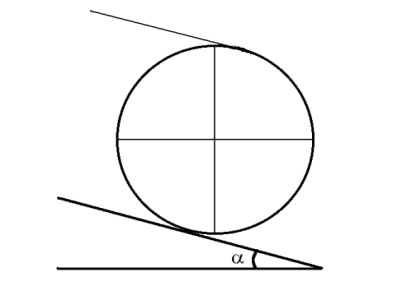 Рис.4 Схема груза Параметры редукторов
Параметры поднимаемого груза
Кинематический расчет редуктора. В редукторе вращение ведущего вала с угловой скоростью ω1 передается на ведомый вал 2 следующим образом. Водило 3, вращаясь с угловой скоростью ω1, приводит в движение систему шестерен 4, 6, закрепленных на общей оси 4-6. Шестерня 4 находится в зацеплении с опорной шестерней 5. Подвижные шестерни 4, 6 совершают спинное движение: вращаясь вокруг оси 4-6 (относительное движение), вместе с этой осью вращение переносится водилом вокруг центральной оси 1-2 редуктора (переносное движение); шестерня 7 находясь в зацеплении с осью 4-6, приводит в движение ведомый вал 2. Расчет кинематики редуктора проводится методом мгновенного центра скоростей. Пусть угловая скорость ведущего вала 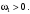 Мгновенная ось абсолютного вращения шестерен 4, 6 проходит параллельно центральной оси 1-2 через точку касания Kшестерни 5 и шестерни 4. Эта точка Мгновенная ось абсолютного вращения шестерен 4, 6 проходит параллельно центральной оси 1-2 через точку касания Kшестерни 5 и шестерни 4. Эта точка 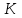 является мгновенным центром скоростей. Так как в рассматриваемой конструкции редуктора мгновенный центр скоростей располагается между осями переносного и относительного движений, то мгновенная ось абсолютного вращения делит расстояние между осями переносного является мгновенным центром скоростей. Так как в рассматриваемой конструкции редуктора мгновенный центр скоростей располагается между осями переносного и относительного движений, то мгновенная ось абсолютного вращения делит расстояние между осями переносного  и относительного движений и относительного движений 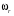 внутренним образом на части, обратно пропорциональные модулям угловых скоростей, скорость результирующего движения равна сумме угловых скоростей составляющих движений внутренним образом на части, обратно пропорциональные модулям угловых скоростей, скорость результирующего движения равна сумме угловых скоростей составляющих движений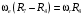 (1) (1)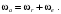 (2) (2)или 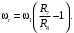 (3) (3)Из (2) и (3) находим скорость абсолютного вращения: 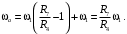 (4) (4)Для определения угловой скорости вращения шестерни 7, и следовательно, и угловой скорости ведомого вала 2 воспользуемся тем, что абсолютные скорости точек шестерен 6 и 7 в точке С их зацепления равны между собой, поскольку нет относительного проскальзывания: 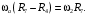 Таким образом, 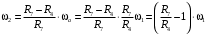 (5) (5)или учитывая, что 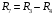 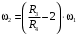 (6) (6)Передаточное число редуктора 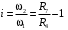 , (7) , (7)или 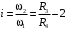 . (8) . (8)Расчет кинетической энергии системы.Кинетическая энергия редуктора вместе с барабаном складывается из энергии ведущего вала и ведущей шестерни 3 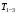 , энергии спаренной шестерни , энергии спаренной шестерни 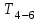 , энергии шестерни 7, вала 2 и барабана. , энергии шестерни 7, вала 2 и барабана.Водило и вал 1 вращаются вокруг неподвижной оси и их кинетическая энергия 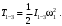 Шестерни 4-6 совершают сложное движение. Поэтому кинетическую энергию шестеренок 4 и 6 найдем как половину произведения момента инерции относительно мгновенной оси вращения и квадрата абсолютной угловой скорости (4). Момент инерции относительно мгновенной оси вращения определяется с помощью теоремы Штейнера 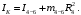 (9) (9)В итоге, 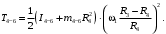 (10) (10)Шестерня 7 с ведомым валом и барабаном вращаются вокруг неподвижной оси и их кинетическая энергия равна 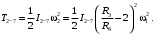 (11) (11)Суммарная кинетическая энергия лебедки 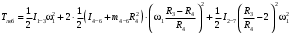 (12) (12)Кинетическая энергия груза определяется по теореме Кенига 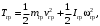 (13) (13)где 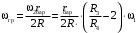 , (14) , (14)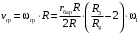 , (15) , (15)rбар – радиус барабана. барабан  R 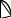 Рис. 4. Барабан и поднимаемый груз (вид сбоку) Кинетическая энергия системы равна сумме кинетических энергий лебедки и груза: 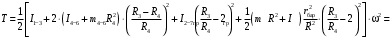 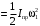 , (16) , (16)где 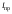 – приведенный момент инерции. – приведенный момент инерции.Вычисление элементарной работы сил, действующих на систему. Работа сил на элементарном перемещении при движении груза без проскальзывания складывается из работы момента, приложенного к барабану, 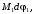 работы момента сопротивления в редукторе, условно приведенного ко второму валу, работы момента сопротивления в редукторе, условно приведенного ко второму валу,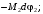 работы силы тяжести груза работы силы тяжести груза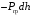 , где , где 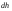 – элементарное изменение высоты центра тяжести груза, работы момента трения качения, действующего на груз, – элементарное изменение высоты центра тяжести груза, работы момента трения качения, действующего на груз,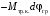 , где , где 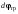 – элементарный угол поворота груза. Все элементарные перемещения, на которых совершается работа, вызваны поворотом вала 1 – элементарный угол поворота груза. Все элементарные перемещения, на которых совершается работа, вызваны поворотом вала 1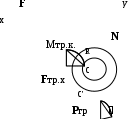 Рис. 5 Плоское движение груза Таким образом,  (17) (17)Отметим, что только работа момента 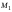 входит с положительным знаком в работу входит с положительным знаком в работу 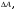 так как моменты так как моменты 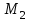 , , 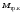 и сила и сила 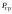 имеют отрицательную мощность. имеют отрицательную мощность.Из соотношений (6) и (14) 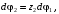 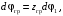 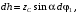 здесь 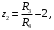 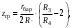 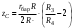 и, следовательно, 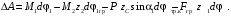 (18) (18)Формула для элементарной работы переписывается следующим образом: 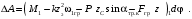 (19) (19)Момент 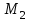 по условию пропорционален угловой скорости по условию пропорционален угловой скорости 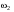 : :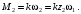 Сила трения качения 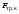 определяется по закону определяется по закону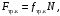 где 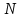 – нормальная составляющая реакции наклонной плоскости на груз. Для ее нахождения требуется рассмотреть уравнения плоскопараллельного движения груза: – нормальная составляющая реакции наклонной плоскости на груз. Для ее нахождения требуется рассмотреть уравнения плоскопараллельного движения груза: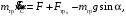 (20) (20)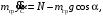 (21) (21)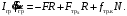 (22) (22)Так как 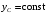 ,то ,то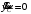 и, следовательно, из уравнения (3.9) и, следовательно, из уравнения (3.9) 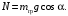 Для нахождения зависимости 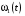 воспользуемся теоремой об изменении кинетической энергии. Cила F является внутренней силой системы и при нерастяжимости троса ее работа равна нулю. воспользуемся теоремой об изменении кинетической энергии. Cила F является внутренней силой системы и при нерастяжимости троса ее работа равна нулю.Дифференциал кинетической энергии имеет вид 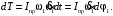 (22) (22)Подставим выражения (19) и (22) в теорему об изменении кинетической энергии 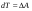 и сократим левую и правую части полученного выражения на и сократим левую и правую части полученного выражения на 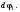 В результате этих действий записываем дифференциальное уравнение для определения угловой скорости первого вала В результате этих действий записываем дифференциальное уравнение для определения угловой скорости первого вала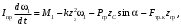 которое является дифференциальным уравнением с разделяющимися переменными и имеет аналитическое решение 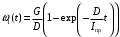 (23) (23)где 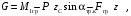 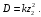 Натяжение свободного участка троса в зависимости от времени.Для нахождения силы натяжения троса F применим теорему об изменении кинетического момента для груза относительно мгновенного центра скоростей – точки 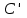 : :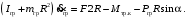 (24) (24)Здесь использовали теорему Штейнера для определения момента инерции относительно оси, проходящей через точку 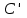 перпендикулярно плоскости рисунка. Зависимость величины перпендикулярно плоскости рисунка. Зависимость величины 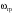 от времени известна, так как от времени известна, так как 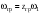 , где угловая скорость , где угловая скорость 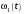 известна из формулы (23). Из формулы (24) находим величину силы F: известна из формулы (23). Из формулы (24) находим величину силы F: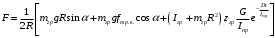 (25) (25)Задание 4 В дифференциальной передаче, расположенной в горизонтальной плоскости, к водилу O1O2 приложен постоянный вращающий момент M. Шестерня 1 весом Q и радиусом R свободно насажена на общую с водилом ось O1 и может вращаться вокруг нее независимо от водила. С шестерней 1 во внешнем зацеплении находится шестерня 2 весом Q и радиусом r. Считая водило однородным стержнем весом P, а шестерни однородными дисками и пренебрегая трением, определить угловые ускорения водила и шестерни 1. За обобщенные координаты принять углы поворота водила ψ и шестерни 1φ. 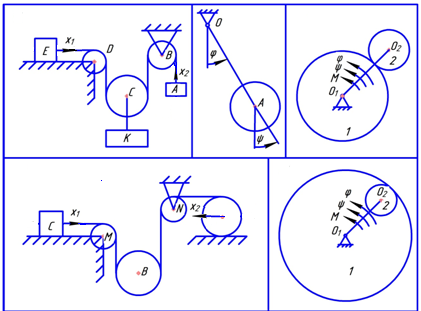 Тела, входящие в систему: шестерня 1 совершает вращательное движение вокруг оси O1, водило и шестерня 2 вращаются вокруг O1. 2. Число степеней свободы s = 2. 3. Обобщенные координаты: q1 = ψ – угол поворота водила, q2 = 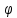 – угол поворота шестерни 1; обобщенные скорости – угол поворота шестерни 1; обобщенные скорости 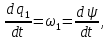 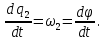 4. Уравнения Лагранжа второго рода: 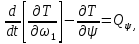 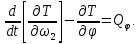 5. Кинетическая энергия системы 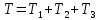 . .Кинетическая энергия водила: 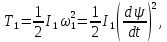 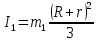 – момент инерции стержня (водила). – момент инерции стержня (водила).Кинетическая энергия шестерни 1: 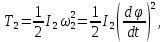 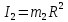 Кинетическая энергия шестерни 2: 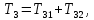 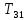 - кинетическая энергия вращения шестерни вокруг оси O1 - кинетическая энергия вращения шестерни вокруг оси O1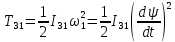 , ,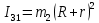 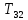 - кинетическая энергия вращения шестерни вокруг оси O2 - кинетическая энергия вращения шестерни вокруг оси O2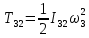 , ,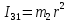 , , 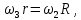 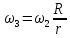 , тогда , тогда 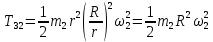 и 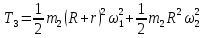 . .Кинетическая энергия системы будет определяться выражением 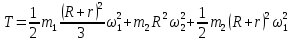 Касательная составляющая силы реакции действующей на шестерню 2 со стороны шестерни 1: 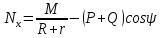 Обобщенная сила соответствующая обобщенной координате 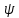 : :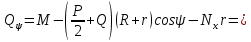 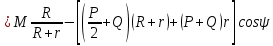 . .Обобщенная сила соответствующая обобщенной координате 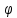 : :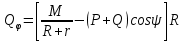 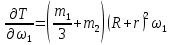 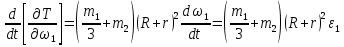 , ,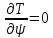 , ,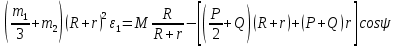 . .для углового ускорения 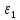 имеем: имеем: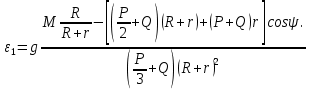 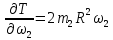 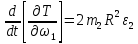 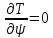 , ,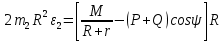 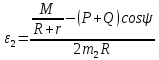 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
