Реферат по предмету Теория систем и системный анализ. Реферат по дисциплине на тему

• Название: Реферат по дисциплине на тему
• Анкор: Реферат по предмету Теория систем и системный анализ
• Дата: 11.03.2022
• Размер: 136.72 Kb.
• Имя файла: Referat.docx
• Тип: Реферат; #391749

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Владимирский государственный университет имени Александра

Григорьевича и Николая Григорьевича Столетовых»

(ВлГУ)

Кафедра «Институт информационных технологий и радиоэлектроники»

Реферат

по дисциплине «»

на тему:

«»

Выполнил:

Проверил:

Владимир 2021

Содержание

Введение.

1. Критерии устойчивости. Понятие устойчивости системы. Условие устойчивости САУ. Алгебраические критерии устойчивости. Критерий Рауса. Критерий Гурвица.

2. Частотные критерии устойчивости. Принцип аргумента. Критерий устойчивости Михайлова. Критерий устойчивости Найквиста.

Введение

Главным вопросом анализа динамических систем управления является решение вопроса об их устойчивости. Техническое понятие устойчивости систем автоматического управления отражает свойство технической системы не только постоянно действовать в нормальных режимах, но и "не отправляться вразнос" при отклонении разнообразных параметров системы от номинала и воздействии на систему дестабилизирующих воздействий, т. способности системе вернуться к равновесному состоянию, из которого она выводится возмущающими или управляющими воздействиями. Устойчивость системы - техническое правило в ряду более трудоемких требований, объединенных с признаками качества и точности САУ.

Критерии устойчивости.

Устойчивость системы.

Система находится в состоянии равновесия, если при отсутствии влияния на систему возмущающих условий ошибка регулирования (разность среди заданным и фактическим состоянием системы) стремится к нулю. Под устойчивостью подразумевается способность динамической системы возвращаться в равновесное состояние после завершения действия возмущения, нарушившего это равновесие. Неустойчивая система после воздействия возмущения удаляется от равновесного состояния или начинает выполнять вокруг него колебания с усиливающей амплитудой. рис. 1

Происхождение неустойчивых (расходящихся) колебаний в системе можно отследить на примере следящей системы с обратной связью(рис. 1). Допустим, что в установившемся состоянии равновесия при опорном сигнале u_o на регуляторе Р выходное состояние объекта управления ОУ равно y_уст . Это состояние поддерживается сигналом рассогласования е_уст , который формируется в регуляторе Р по разности основного сигнала и сигнала обратной связи у_ос-уст , т.е. е_уст = u_o -у_ос-уст. В первый момент введения системы в силу инерционности обратной связи у_ос = 0, а, следовательно, e(t) >> е_уст , что вызывает нарастание выходной величины y(t), что будет стремиться к y(t) >> у_уст по крайней мере, до тех пор, пока сигнал обратной связи не начнет уменьшать значение e(t). Впрочем основательно возросшая значение y(t) через ОС передается на вход регулятора системы и может настолько кардинально сбавить значение e(t), что это может привести к дальнейшему понижению величины выходного сигнала до значений y(t) << у_уст , т. к возникновению колебательного процесса относительно равновесного состояния. При неблагоприятном соотношении параметров системы колебательный ход может быть незатухающим и даже расходящимся. случай подобного процесса в концертной акустике хорошо знаком – свист из динамиков, когда показатель оборотной связи от динамиков на микрофоны на определенных частотах становится положительным.

Устойчивость линейной системы обусловливается не характером возмущения, а структурой самой системы. Говорят, что система устойчива "в малом", если определен факт присутствия устойчивости, но не определены ее границы. Система устойчива "в большом", когда назначены границы устойчивости и то, что реальные отклонения не выходят за эти границы. Соответственно, и задача изучения систем на устойчивость может быть поставлена двояко:

1) устойчива ли система при заданном значении ее параметров;

2) в каких диапазонах можно изменять параметры системы, не нарушая ее устойчивости.

Вторая задача изучения имеет место при наладке и эксплуатации систем автоматического управления.

В соответствии с классическим способом решение дифференциального уравнения для системы ищется в виде:

y(t) = Усв(t) + Увын(t). (Рис. 1)

Усв(t) – свободная составляющая, общее решение однородного дифференциального уравнения с нулевой правой частью:

a₀ y⁽ⁿ⁾ + a₁ y^(n-1) + ... + _an-1 y’ + a_ny=0,

т.е. когда все внешние воздействия сняты, и состояние системы определяются лишь собственной структурой.

Функция у_вын (t) представляет собой частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t). Поэтому вторая составляющая общего решения называется вынужденной. Она определяет вынужденный установившийся режим работы системы при наличии на входе определенного воздействия u(t) или f(t) после окончания переходного процесса.

Рис. 2.

Можно провести аналогию между САУ и пружиной, колебания которой описываются подобным дифференциальным уравнением (Рис.2). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии с независимой составляющей решения уравнения, характер колебаний будет определяться исключительно структурой самой пружины. Ежели подвесить к пружине груз, то на свободные колебания наложится наружная сила Р. После затухания колебаний, обрисовываемых исключительно свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей У_вын = У(t^®∞). Если внешнее воздействие само будет изменяться по синусоидальному закону P = P_o sin(wt+j), то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть у_вын = y_maxsin(wt+j).

Только стабильная система является работоспособной. Основы строгой концепции устойчивости динамических систем были разработаны акад. А.М. Ляпуновым в работе «Общая задача об устойчивости движения» (1892 г.) Понятия о устойчивости, вытекающие из этой работы, заключаются в следующем.

Когда система описывается линейным дифференциальным уравнением, то ее надежность не зависит от величины возмущения. Линейная система, стабильная при малых возмущениях, будет устойчива и при больших. Нелинейные системы могут быть устойчивы при небольших возмущениях и неустойчивы при больших.



Наглядное представление о системах, стабильных при малых и неустойчивых при больших возмущениях, дает поведение шара во впадине на рисунке сверху. При малых влияниях на шар и его малых отклонениях не выше края впадины шар возвращается в начальное положение и система шар - поверхность устойчива. При больших влияниях с отклонением за край впадины шар не возвращается в исходное положение - система неустойчива. следовательно надежность систем изучается раздельно для случая малых и больших возмущений.

Проблема стабильности обычно появляется в замкнутых системах из-за воздействия обратной связи. Потому в будущем устойчивость исследуется на примерах изолированных систем, хоть методы исследования устойчивости универсальны.

Условие устойчивости САУ.

Применительно к сигналам в САУ частное решение для вынужденной составляющей обычно имеет простой вид, не влияющий на устойчивость. Вопрос устойчивости сводится к выяснению устойчивости свободного движения системы и требует анализа характера решения уравнения свободного движения, составленного относительно отклонения выходной величины y(t) от установившегося состояния.

Как известно, передаточная функция любой линейной динамической системы может быть приведена к виду:

W(p) = K(p)/H(p) = [b₀ p^m +b₁ p^m-1 +…+b_m-1 p+b_m ] / [a₀ pⁿ +a₁ p^n-1 +…+ a_n-1 p+a_n ]

(2.1)

Где a и b - постоянные коэффициенты, которые представляют собой вещественные числа и выражаются через конкретные физические параметры элементов системы. Полином К(р) может не содержать членов с оператором р и представлять собой произведение коэффициентов передачи звеньев, образующих систему.

Важнейшим свойством выражения (2.1) является условие n≥m, т. е. порядок полинома Н(р) знаменателя передаточной функции не ниже порядка полинома К(р) ее числителя. Это условие вытекает из физических свойств звеньев реальных динамических систем.

Из выражения (2.1) передаточной функции системы можно получить дифференциальное уравнение системы в целом, как в разомкнутом, так и в замкнутом состоянии.

Уравнения разомкнутых систем.

Если выражение (2.1) является передаточной функцией разомкнутой системы, то выражение

u(р) К(р) = y(p) Н(р). (2.2)

будет представлять собой операторное уравнение разомкнутой системы (уравнение в изображениях переменных). Положив в (2.2) u(p)=0, получим операторное уравнение свободного движения в разомкнутой линейной динамической системе:

y(p) H(p) = 0. (2.3)

Переходя в (2.3) к оригиналам, т. е. от операторного уравнения к дифференциальному, и обозначив y(t) = х, получаем дифференциальное уравнение свободного движения в разомкнутой линейной динамической системе

a₀dⁿx/dtⁿ + a₁d^n-1x/dt^n-1+…+a_n-1dx/dt +a_n = 0 (2.4)

Характеристическим уравнением, соответствующим дифференциальному уравнению (2.4), будет

Н(р) = 0, a₀pⁿ +a₁p^n-1+…+a_n-1p+a_n = 0. (2.5)

Отсюда следует: приравненный нулю знаменатель передаточной функции разомкнутой линейной динамической системы является характеристическим уравнением, соответствующим дифференциальному уравнению разомкнутой системы. В связи с этим многочлен Н(р)=0 называется характеристическим оператором системы.

Уравнение замкнутых систем.

Пусть (2.1) является передаточной функцией разомкнутой системы. Для замкнутой системы в силу отрицательной главной обратной связи имеем u(t) = -y(t), и (2.2) принимает вид -К(р) y(р) = Н(р) y(р). Операторное уравнение свободного движения в замкнутой системе:

[К(р)+Н(р)]y(р) = 0, (2.6)

где К(р), Н(р) - соответственно числитель и знаменатель передаточной функции разомкнутой системы; y(р) — изображение координаты системы в точке ее замыкания.

На основании (2.6) можно записать характеристическое уравнение, соответствующее дифференциальному уравнению свободного движения в замкнутой системе:

К(р) + Н(р) = 0. (2.7)

учетом того, что W_oc(p) = 1, передаточная функция замкнутой системы:

W_зс(p) = W(p)/[1 + W(p)], (2.8)

где W(p)=K(p)/H(p) - передаточная функция разомкнутой системы.

Или:

W_зс (p) = K(p)/[K(p) + H(p)] = K(p)/H_зс (p). (2.8)

На этом основании характеристическое уравнение замкнутой системы можно записать в виде

H_зс (р) = K(p) + H(p) = 0. (2.9)

Следовательно, приравненная нулю сумма полинома числителя и полинома знаменателя передаточной функции разомкнутой системы или приравненный нулю полином знаменателя передаточной функции замкнутой системы являются характеристическим уравнением, соответствующим дифференциальному уравнению свободного движения в замкнутой системе.

Корни характеристических уравнений систем могут быть либо вещественными, либо попарно комплексно сопряженными. Решение однородного уравнения выражается через корни характеристического уравнения и коэффициенты перед экспонентами, которые могут быть вычислены через вычеты:

у_св(t) = С_n exp(p_nt). (2.10)

Условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанного в отклонениях, должна стремиться к нулю, то есть затухать.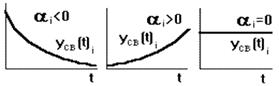

(Рис. 3)

Из формулы (2. 10) легко вывести условие устойчивости линейных динамических систем: линейная система будет устойчива, если все вещественные корни и все вещественные части единых корней характеристического уравнения, соответствующего исходному дифференциальному уравнению независимого хода системы, будут отрицательными, что приносит затухающие по экспоненте решения. Если присутствуют чисто мнимые корни, то в переходном процессе будут гармонические незатухающие составляющие.

Каждому отрицательному вещественному корню a_i соответствует экспоненциально затухающая во времени составляющая у_св(t)_i , каждому положительному - экспоненциально расходящаяся, каждому нулевому корню соответствует у_св(t)_i =const (Рис. 3).

(Рис.4)

Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой wi , при положительной вещественной части - расходящиеся колебания, при нулевой - незатухающие (рис. 4).

(Рис.5)

Исходя из положения на единой плоскости, корни с отрицательными вещественными частями именуются левыми, с положительными - правыми (Рис.5). Следовательно условие устойчивости линейной САУ можно сконструировать следующим образом: для того, чтобы система была устойчива, нужно и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хоть один корень правый, то система неустойчива. Если один из корней равен нулю, а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система располагается на границе колебательной устойчивости. Таким образом, исследование устойчивости системы сводится к определению знаков вещественных частей корней характеристического уравнения системы. Но решение уравнений четвертой и более высоких степеней может встречать затруднения. Поэтому применяются косвенные методы анализа устойчивости без определения корней характеристического уравнения, по определенным критериям устойчивости.

Проверку факта отрицательности вещественных частей корней можно выполнять тремя способами:

- вычислив корни непосредственно, с использованием готовых программ;

- связав расположение корней с коэффициентами характеристического уравнения для последующего аналитического исследования;

- судить об устойчивости по частотным характеристикам системы.

Первые два способа называют алгебраическими, последний - частотным. В инженерной практике необходимо иметь эффективные и удобные правила проверки устойчивости. Однако сам по себе критерий устойчивости не обязан быть необходимым и достаточным условием устойчивости системы.

1. 
   Алгебраические критерии устойчивости.
   

Необходимое условие устойчивости.

Если все корни характеристического уравнения левые (вещественные части всех корней отрицательны), то все коэффициенты уравнения имеют один знак, т.е. все значения a_n либо больше нуля, либо меньше нуля одновременно. Равенство коэффициентов нулю не позволяется (граница устойчивости). Основание очень простое и заключается в разложении полинома на простейшие множители. Они могут являться вещественные или комплексно - сопряжённые. Соединим последние в пары и перемножим, при этом в скобках нет ни одного отрицательного числа, а, следовательно, знак всех членов характеристического уравнения будет определяться знаком коэффициента a₀. В дальнейшем будем рассматривать только уравнения, где a₀ > 0. В противном случае уравнение умножается на -1.

Осмотренное условие при порядке системы более 2 является необходимым, однако не достаточным условием, и используется для отсеивания заранее неустойчивых систем. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.

Критерий Рауса.

Используется в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке – аналогично коэффициенты с нечетными индексами;

3) остальные элементы таблицы определяется по формуле:

c_k,i = c_k+1,i-2 - r_ic_k+1, _i-1, где r_i = c_1,i-2 /c_1,i-1

i ≥3 - номер строки, k - номер столбца.

4) Число строк таблицы на единицу больше порядка характеристического уравнения.

r	i\k	1	2	3	4
-	1	c11=a0	c21=a2	c31=a4	…
-	2	c12=a1	c22=a3	c32=a5	…
r3=c11\c12	3	c13=c21-r3c22	c23=c31-r3c32	c13=c21-r3c22	…
r4=c12\c13	4	c14=c22-r4c23	c24=c32-r4c33	c13=c21-r3c22	…
…	…	…	…	…	…

Чтобы система была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса c₁₁ , c₁₂ , c₁₃ ,... были положительными. Если это не выполняется, то система неустойчива, а количество правых корней равно числу перемен знака в первом столбце.

Достоинство - критерий прост в использовании независимо от порядка характеристического уравнения. Он удобен для использования на ЭВМ. Его недостаток - маленькая наглядность, нелегко рассуждать о степени стабильности системы, насколько далеко отстоит она от рубежа устойчивости.

(Рис. 6)

Критерий Гурвица.

 Гурвиц порекомендовал непохожий критерий устойчивости. Из коэффициентов характеристического уравнения основывается опознаватель Гурвица D по алгоритму:

1) по основной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an ;

2) от каждого элемента диагонали вверх и вниз достраиваются столбики определителя так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.

Чтобы система была устойчива, нужно и достаточно, чтобы все коэффициенты характеристического уравнения и все n основных диагональных миноров матрицы Гурвица были положительны. количество определителей Гурвица равно порядку характеристического уравнения п.

Критерий Гурвица используют при n ≤ 5. При больших порядках увеличивается число определителей, и процесс становится трудоемким. Недостаток критерия Гурвица - малая наглядность. преимущество - комфортен для реализации на ЭВМ.

ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ

Частотные способы изучения стабильности основаны на связи местоположения корней характеристического полинома (обозначим его функцией D(р) для каждого типа систем) с годографом данного полинома на комплексной плоскости, т. с графиком комплексной функции D(jw) при изменении w от 0 до ∞. Это графоаналитические методы, позволяющие по виду частотных характеристик систем рассуждать об их устойчивости. Их достоинство - в несложной геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.

Принцип аргумента.

Запишем характеристический полином в виде

D(p) = a₀ (p-p₁ ) (p-p₂ )… (p-p_n ) = 0,

Его корни: p_i = a_i + jw_i = |p_i | exp(j arg(p_i )), где arg(p_i ) = arctg(w_i /a_i ) + kp, |p_i | - значения модулей корней.

(Рис 7.)

Каждый корень можно представить вектором на комплексной плоскости (рис. 7а), дальше отличие p - p_i представится разностью векторов (рис. 7), где p - любое число.

Ежели менять значение p случайным образом, то конец вектора p - p_i будет передвигаться по комплексной плоскости, а его начало будет оставаться неподвижным, так как p_i - это четкое постоянное значение. В частном случае, если на вход системы давать гармонические колебания с различной частотой w, то p = jw, а характеристический полином воспринимает вид:

D(jw) = a₀ (jw - p₁ ) (jw - p₂ ) ... (jw - p_n ).

При этом концы векторов jw - p_i будут пребывать на мнимой оси (рис. 7в). Если изменять w от -∞ до +∞, то любой вектор jw - p_i будет вращаться относительно своего основания p_i на угол +p для левых и -p для правых корней (рис. 7г).

Характеристический полином можно представить в виде

D(jw) = |D(jw)| exp(j arg(D(jw))),

где |D(jw)| = a₀ |jw-p₁ | |jw-p₂ | ... |jw-p_n |, arg(D(jw)) = arg(jw-p₁ ) + arg(jw-p₂ ) + ... + arg(jw-p_n ).

Пусть из n корней m - правые, а n-m - левые, тогда угол поворота вектора D(jw) при изменении w от -∞ до ∞ равен

=(n-m)p - mp,(3.1)

или при изменении w от 0 до +∞:

 = (n - 2m) (p/2) (3.2)

Отсюда выливается правило: изменение аргумента вектора D при изменении частоты от -∞ до +∞ равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на p, а при изменении частоты от 0 до +∞ эта разность умножается на p/2.

Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее известных критерия: критерий Михайлова и критерий Найквиста.

Критерий устойчивости Михайлова

Так как для устойчивой системы число правых корней m = 0, то угол поворота вектора D(jw) составит

= np/2 (3.3)

(Рис 8.)

Концепция будет устойчива, когда вектор D(jw) при изменении частоты от 0 до +∞ обернется на угол np/2. При этом конец вектора опишет кривую, именуемую годографом Михайлова. Для построения годографа выражение (4.1.6) заносится с заменой p на jw в форме:

a₀ pⁿ +a₁ p^n-1 +…+ a_n-1 p+a_n = D(jw ) = P(w) + jQ(w),

где P(w) - вещественная часть, как сумма всех членов характеристического уравнения, сохрняющих j в четных степенях, Q - мнимая часть выражения. Годограф начинается на положительной полуоси при D(0) = a_n , и, при изменении частоты от 0 до ∞, последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, с уходом в бескрайность в n-ом квадранте (рис. 8а).

Если такое правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается очередь прохождения квадрантов (рис. 8б)), то подобная система неустойчива - это и есть важное и достаточное условие устойчивости по критерию Михайлова.

Критерий кофмортен своей наглядностью и используется, когда известно уравнение изолированной системы. Если кривая проходит поблизости начала координат, то система располагается вблизи границы устойчивости и наоборот.

(Рис 9.)

Критерий устойчивости Найквиста.

Данный критерий устроен на связи свойства устойчивости замкнутой системы с формой АФЧХ разомкнутой устойчивой системы. Разомкнутой системой являются все поочередно объединенные блоки от входа системы до точки замыкания возвратной связи (рис.9) Исследование разомкнутой системы проще, чем замкнутой, и его возможно производить экспериментально.

Передаточная функция W_pc разомкнутой системы:

W_pс (jw) = K_p c (jw)/H_pc (jw),

с углом поворота фазы в соответствии с выражением (3.2):

D arg H_рс (jw) = np/2, 0 ≤ w ≤ ∞. (3.3)

АФЧХ замкнутой системы описывается выражением:

W_зс (jw)= W_pc (jw) /[1+ W_pc (jw)]. (3.4)

Обозначим знаменатель этого выражения через W₁ (jw):

W₁ (jw)=1+W_pc (jw)=1+K_p c (jw)/H_pc (jw)=H(jw)/H_pc (jw), (3.5)

где H(jw) = K_pc (jw) + H_pc (jw), характеристический полином замкнутой системы при р=jw.

В соответствии со свойствами передаточных функций порядок полинома Н(р) не превышает порядка полинома H_pc (p), т.к. H(p)=K_pc (p)+H_pc (p), а порядок полинома K_pc (p) меньше порядка полинома H_pc (p). Поэтому критерий Михайлова для замкнутой системы соответствует выражению:

D arg H(jw) = (n - 2m) (p/2), 0 ≤ w ≤ ∞. (3.6)

где m - число правых корней системы, имеющей в замкнутом состоянии характеристический полином Н(р)=0.

Из следует:

D arg W₁ (jw) = D arg H(jw) - D arg H_pc (jw).

D arg W₁ (jw) = (n - 2m) (p/2) - np/2 = -mp. (3.7)

В устойчивой замкнутой системе правых корней в характеристическом уравнении нет, т. е. m=0, а, следовательно, условием устойчивости замкнутой системы будет:

D arg W₁ (jw) = 0. (3.8)

Условие (3.8) проделавается только тогда, когда кривая W₁ (jw) при изменении частоты от 0 до ∞ не охватывает начала координат комплексной плоскости. Действительно, исключительно в этом случае результирующий поворот вектора W₁ (jw) при изменении w от 0 до ∞ будет равен нулю, так как увеличение угла j(w), обусловленное ходом вектора W₁ (jw) в положительном направлении (против часовой стрелки), будет компенсироваться таким же убыванием j(w), обусловленным ходом вектора W₁ (jw) в отрицательном направлении (по часовой стрелке).

Как видно из (3.5), переход на комплексной плоскости от годографа вектора W₁ (jw) к годографу вектора АФЧХ разомкнутой системы W_pс (jw) исполняется сдвигом искривленной W₁ (jw) влево на -1, так как W_pc (jw) = W₁ (jw) -1. С учетом этой операции, приобретаем следующую формулировку амплитудно-фазового аспекта устойчивости Найквиста: линейная динамическая система, стабильна в разомкнутом состоянии, устойчива и в замкнутом состоянии, если АФЧХ разомкнутой системы W_pс (jw) при изменении частоты от 0 до ∞ не обхватывает на комплексной плоскости точку с координатами (-1; j0) (рис. 109, годограф 2).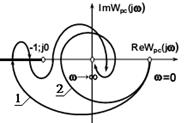

(Рис.9)

Более общая формулировка аспекта Найквиста причисляется к системам, имеющим так нарекаемую АФЧХ второго рода (рис. 4, годограф 1), когда W_pс (jw) пересекает (неограниченное множество раз) вещественную ось левее точки Re W_pc (w) = -1. Будем думать положительным переход годографа сквозь вещественную ось, если он совершается сверху вниз, и отрицательным, если он совершается снизу вверх. Для таких годографов критерий Найквиста формулируется в следующем виде: линейная динамическая система, стабильная в разомкнутом состоянии, устойчива и в замкнутом состоянии, если при изменении частоты от 0 до +∞ отличие среди положительных переходов годографа АФЧХ разомкнутой системы через участок вещественной оси (-1; -∞) и числом отрицательных переходов равна нулю. Из этого условия видно, что система, устойчивая в разомкнутом состоянии и имеющая АФЧХ в форме кривой 1 на рис. 10, устойчива и в замкнутом состоянии.

(Рис.10)

На рис. 10а приведены АФЧХ разомкнутых САУ, устойчивых в замкнутом состоянии, на рис. 10б - замкнутая САУ неустойчива.

На рис. 10в и 10г показаны АФЧХ разомкнутых астатических САУ, соответственно устойчивых и неустойчивых в замкнутом состоянии. Их особенность в том, что АФЧХ при w ® 0 уходит в бесконечность. В этом случае при использовании критерия Найквиста ее мысленно замыкают на вещественную ось по дуге окружности бесконечно большого радиуса.

Критерий Найквиста нагляден. Он позволяет не только выявить, устойчива ли система, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.