физика. Физика. Решение 81. По прямому проводнику длиной 1 м течет ток I100 А. Определить индукцию. В магнитном поле в точке

Название	Решение 81. По прямому проводнику длиной 1 м течет ток I100 А. Определить индукцию. В магнитном поле в точке
Анкор	физика
Дата	15.03.2023
Размер	0.62 Mb.
Формат файла
Имя файла	Физика.docx
Тип	Решение #991983

81. По прямому проводнику длиной ι=1 м течет ток I=100

А. Определить индукцию. В магнитном поле в точке,

равноудаленной от концов проводника и находящейся на

расстоянии b=0,5 м от него.

Решение:

механический момент N=I*S*B*sin(a), где S=a*a*=a^2.

Для потенциальной энергии W=I*S*B*cos(a).

Выразим из первой формулы sin(a): sin(a)=N/(I*a^2*B).
Теперь выразим cos(a): cos(a)=(1-sin(a)^2)^0.5=( 1-( N/(I*a^2*B) )^2 )^0.5.

Подставим cos(a) в формулу для потенциальной энергии:
W=I*a^2*B*cos(a)=I*a^2*B*cos(a)=( (I*a^2*B)^2-N^2)^0.5.

Размерность выражения выше (А*м^2*Тл)=А*м^2*Н/(А*м)=Н*м=Дж. Для момента — та же размерность, поэтому выражение для W имеет размерность энергии и равно

W= ((50*0.01*1) ^2-0.25^2) ^0.5=0.43 Дж.

92. Плоский проводящий контур с площадью S=50 см2

помещен в однородное магнитное поле, индукция которого

В=4 Тл. Сопротивление контура R=1 Ом. Плоскость контура

составляет угол α=30° с линиями магнитной индукции.

Определить величину заряда q, который пройдет по контуру

при включении магнитного поля.

Решение:

S = 50 см^2 = 0,005 м^2.

B1 = 4 мТл = 4 * 10^-3 Тл.

B2 = 0 Тл.

R = 1 Ом.

∠γ = 30°.

q - ?

Запишем закон электромагнитной индукции Фарадея: ЭДС = - ΔФ/t, где ЭДС - электродвижущая сила, ΔФ - изменение магнитного потока, t - время изменения магнитного потока.

ΔФ = Ф2 - Ф1.

Ф1 = В1 * S * cosα.

Ф2 = В2 * S * cosα.

∠α = 90° - ∠γ = 60°.

ЭДС = - ΔФ/t = - (Ф2 - Ф1) / t = (В1 * S * cosα - В2 * S * cosα) / t = (В1 - В2) * S * cosα/t.

Запишем закон Ома: I = ЭДС/R = (В1 - В2) * S * cosα/t * R.

I = q/t.

q/t = (В1 - В2) * S * cosα/t * R.

q = (В1 - В2) * S * cosα/R.

q = (4 * 10^-3 Тл - 0 Тл) * 0,005 м^2 * cos60°/1 Ом = 1 * 10^-5 Кл.

Ответ: q = 1 * 10^-5 Кл.

100. На дифракционную решетку, содержащею N=250 штрихов

на миллиметр, падает нормально белый свет, а затем

проецируется помещенной внутри решетки линзой на экран.

Расстояние от линзы до экрана L=1,2 м. Границы видимого

спектра: λкр=0,780 мкм и λф=0,400 мкм. Определить ширину

спектра первого порядка на экране.

Решение:__106'>Решение:

N=600

1=1

L=1.2m

Λф=400нм

Λк=780нм

х=?

103. Пучок естественного света, последовательно проходя через

два николя, ослабляется в 6 раз. Принимая, что коэффициент

поглощения каждого николя R=0,1, найти угол φ между

плоскостями пропускания николей.

Решение: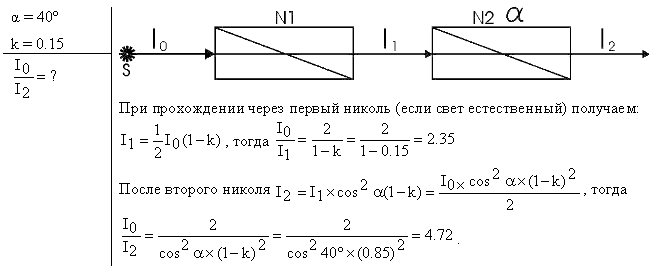

106. Вычислить энергию W, изучаемую в поверхности S=1 м2

абсолютно черного тела за время t=10 мин, если известно, что

максимум спектральной плоскости энергетической

светимости приходиться на длину волны λmax=460 нм.

Решение:

114. На серебряную пластинку падает монохроматический свет.

Фототок прекращается при минимальной задерживающей

разности потенциалов Umin=0,75 В. Определить длину волны

падающего излучения, если работа выхода электронов из

серебра А вых =4,7 эВ

Решение:

Подставляем числа λ =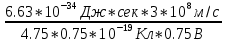

=0.00000000000992*10^-7=992м

117. Свет падает нормально на зеркальную поверхность,

находящуюся на расстоянии r=0,2 м от точечного

монохроматического источника мощностью P=220 Вт.

Определить давление, оказываемое светом на зеркальную

поверхность. Считать, что вся мощность источника

расходуется на излучение.

Решение:

Подставляем числа P=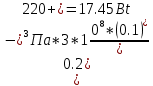

121. Найдите длину волны фотона, который испускается при

переходе атома водорода из состояния n=9 в основное

состояние.

Решение:

132. Одновременно определяется положение и импульс

электрона с образованной энергией 2,00 кэВ. Если его

положение определяли с точностью 1,00Å, то с какой

точностью (в процентах) можно определить при этом его

импульс?

Решение:

Δp

Δх=2pih/2

Δр=pih/Δ х=3.14*6.62е-34/1е-10=5.27е-25 кг м/с

p=mv=(2Em).^0.5=(2*4.81е.^-16*9.11e-31).^0.5=2.41e-23 кг м/с=241.46e-24 кг м/с

Относительная погрешность равна:

n=(Δр/р)*100=(5.27/241.46)*100=2.18%

140. Определить расстояние между атомными плоскостями

кристалла, если при дифракции на нем пучок электронов дает

второй дифракционный максимум под углом Θ=65°

Решение: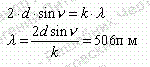

154. Покажите, что э. д. с. Холла дается формулой ξн= υgBb, где

υg=-скорость дрейфа относительных зарядов в плоском

проводнике шириной b.

Решение:

В=В₁+В

Магнитная индукция полей, создаваемых бесконечно длинными прямыми проводниками с током I₁ и I₂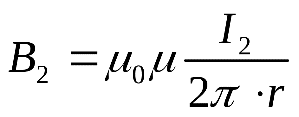

где μ₀ – магнитная постоянная; μ- магнитная проницаемость среды.

Подставив выражение (2) в формулу (1) и учитывая, что I₁=I₂=I и μ=1 (для вакуума), получим искомое выражение для магнитной индукции в точке А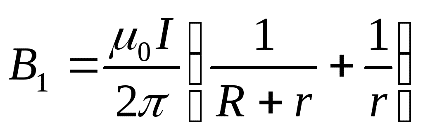

157. Во сколько раз возрастает сопротивление из чистого

германия, если его температуру понизить с 300К до30 К?

Решение:

Удельная проводимость собственных полупроводников
γ=γ0e-∆W2kT
k – постоянная Больцмана;
T – термодинамическая температура.
Тогда
ρ1ρ2=γ2γ1=e-∆W2kT2e-∆W2kT1=e-∆W2k1T2-1T1
Следовательно
ρ1ρ2=e-1,300∙10-192∙0.30∙10-23Ответ: 586
Сопротивление образца уменьшится в 586раз

146. Определить, какую минимальную энергию должен иметь нейтрон, чтобы пошла реакция

¹₀n + ¹⁶₈O + 2,2 МэВ à ¹³₆C + ⁴₂He.

Решение:

(Tn )min ≈ |Q| 1 +=M16 O939,57МэВ ≈= 2,216 1 +8 · 939,57 + 8 · 938,27 − 28,30≈ 2,216 (1 + 0,063) МэВ ≈ 2,36 МэВ

Период полураспада ¹³⁸₉₂U (относительно β-распада) T_1/2 = 4, 50·10⁹ лет. Сколько распадов в 1 секунду происходит в 1,00 г²³⁸₉₂U?

Решение:

При

< (45

49) Е_акт = 0 и самопроизвольное деление возможно только за счет туннельного эффекта. Это явление назвали спонтанным делением.

Активность спонтанного деления: