лополлоп. контр физ. Решение а заполнение конденсатора диэлектриком производится до отключения конденсатора от источника напряжения
 Скачать 3.33 Mb. Скачать 3.33 Mb.
|
|
Тема 1 задача 6 На пластины плоского конденсатора, расстояние между которыми d = 3 см, подана разность потенциалов U = 1 кВ. Пространство между пластинами заполняется диэлектриком (ε= 7). Найти поверхностную плотность связанных зарядов. Задачу решить, если заполнение конденсатора диэлектриком производится: а) до отключения конденсатора от источника напряжения; б) после отключения. Дано: d = 3 см = 0,03м ε = 7 ε0= 8,85 *10-12Ф/м U = 1 кВ = 1000 В Найти: σ - ? Решение. а) заполнение конденсатора диэлектриком производится до отключения конденсатора от источника напряжения. Напряженность поля в диэлектрике Е уменьшается в Е раз по сравнению с напряженностью поля в вакууме Е0: Е = Е0/ε , (30) Напряженность поля между пластинами плоского конденсатора в вакууме равна: E0 = U/d (31) где U - разность потенциалов; d - расстояние между пластинами. Следовательно, напряженность поля в дизлектряке^ E = U/εd (32) Напряженность этого поля определит вектор поляризацяи P: P= (ε -1)ε0 E (33) В однородном и изотропном диэлектрике вектора и совпадают по направлению, а нормальная составляющая вектора поляризации равна модулю вектора Р. Следовательно: Pn = (ε -1)ε0 E (34) Используя выражение (32) и лодставляя его в выражение (34), получим: Pn = (ε -1)ε0 U/ εd (35) С другой стороны нормальная составляющая вектора поляризации равна поверхностной плотности связанных зарядов σ, т.е. σ = Pn = (ε -1)ε0 U/ εd (36) Вычислелния: σ = (7-1)*8,85 *10-12* 1000/7*0,03 = 2,53*10-7Кл/м2 а) заполнение конденсатора диэлектриком производится после отключения конденсатора от источника напряжения. На пластинах конденсатора будет накоплен заряд, равный: q=CU, (37) где C– емкость конденсатора,U– напряжение, подаваемое на его пластины. Поверхностная плотность харяда в этом случае будет вычислятся по формуле: σ = q/S, (38) где q– заряд,S– площадь пластин. Выразим площадь пластин из формулы электроемкости плоского конденсатора: С = εε0 S/d ==> S = Cd/ εε0 (39) Подставляя выражения (37) и (39) в (38), получим: σ = СUεε0/Cd=Uεε0/d(40) Вычисления: σ = 1000*7*8,85 *10-12/0,03 = 2,065*10-6Кл/м2 Ответ: а) σ 2,53*10-7Кл/м2 б)σ =2,065*10-6Кл/м2 Тема 2 задача 1 Задача 2 КАК ПРИМЕР Дано:t1=2000∘ C, R1=204 Ом, t2=20∘ C, R2−? Решение задачи:Известно, что зависимость сопротивления проводника от температуры описывается следующей формулой: R=R0(1+αt) Здесь R – искомое сопротивление при температуре t, R0 – сопротивление при температуре t0 (в данном случае t0=0∘ C), α – температурный коэффициент сопротивления, равный для вольфрама 0,0046 1/°C, t – температура (в градусах Цельсия), при которой нужно найти сопротивление проводника Известно, что сопротивление вольфрамового проводника при температуре t1 равно R1, а при температуре t2 равно R2, поэтому можем получить такую систему: {R1=R0(1+αt1)R2=R0(1+αt2) Нижнее равенство поделим на верхнее, тогда: R2R1=1+αt21+αt1 Откуда получим искомое сопротивление R2: R2=R11+αt21+αt1 Посчитаем численный ответ этой задачи: R2=204⋅1+0,0046⋅201+0,0046⋅2000=21,8Ом формулу напишу словами: искомое сопр. равно дроби, в числителе 260, в знаменателе единица плюс альфа, умноженная на дельта Т, у вас дельта Т= 2900-20=2880. ЗАДАЧА 3 Дано: R1=10 Ом, R2=20 Ом, R3=30 Ом, U1=20 В, U−? Решение задачи: 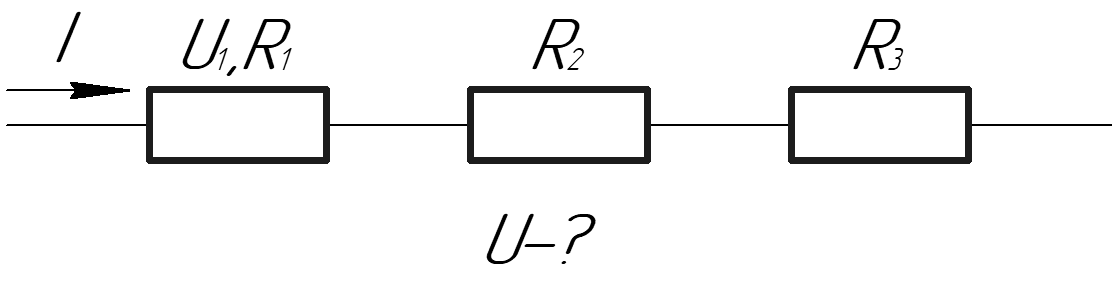 Напряжение на концах цепи можно найти из закона Ома: U=IR(1) Здесь R – общее сопротивление цепи, которое в случае трёх последовательно соединенных сопротивлений R1, R2 и R3 можно определить по формуле: R=R1+R2+R3(2) Зная падение напряжения U1 на первом сопротивлении R1, используя тот же закон Ома для участка цепи, легко найти ток I в цепи: I=U1/R1(3) Подставим (2) и (3) в формулу (1), тогда: U=U1(R1+R2+R3)/R1 Численный ответ равен: U=20⋅(10+20+30)/10=120В РЕКЛАМА Ответ: 120 В. Задача 4 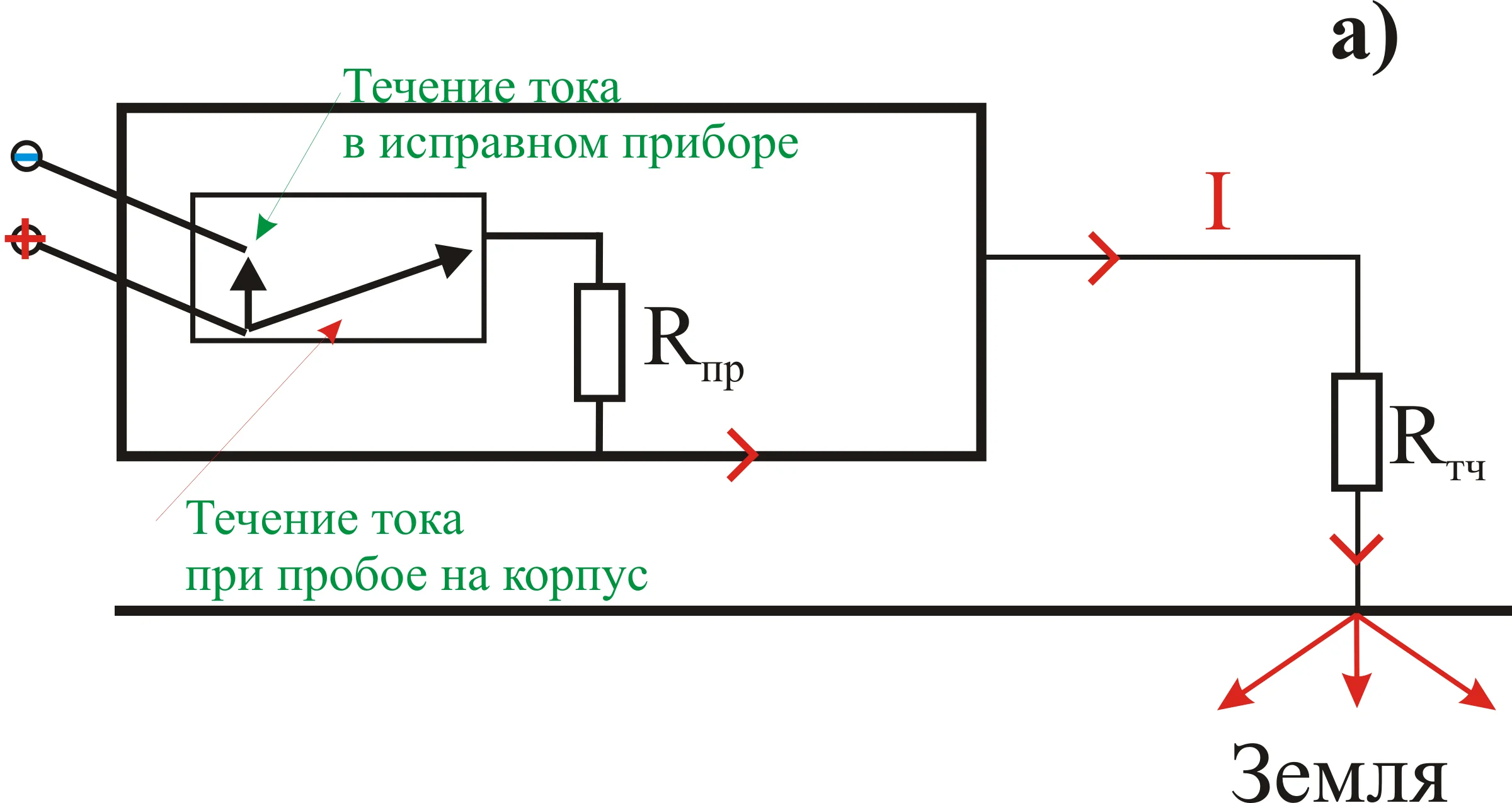  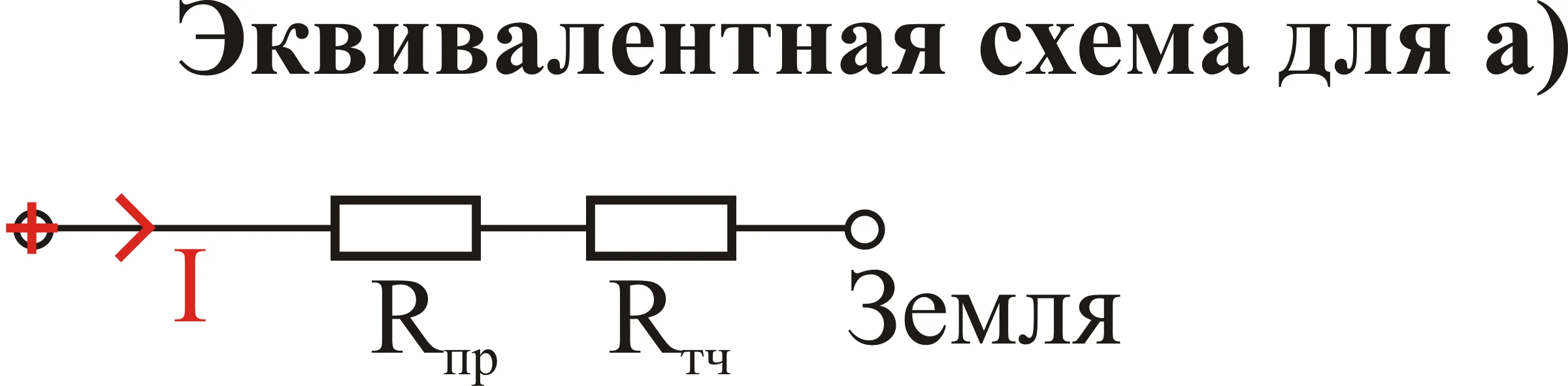     Задача 5 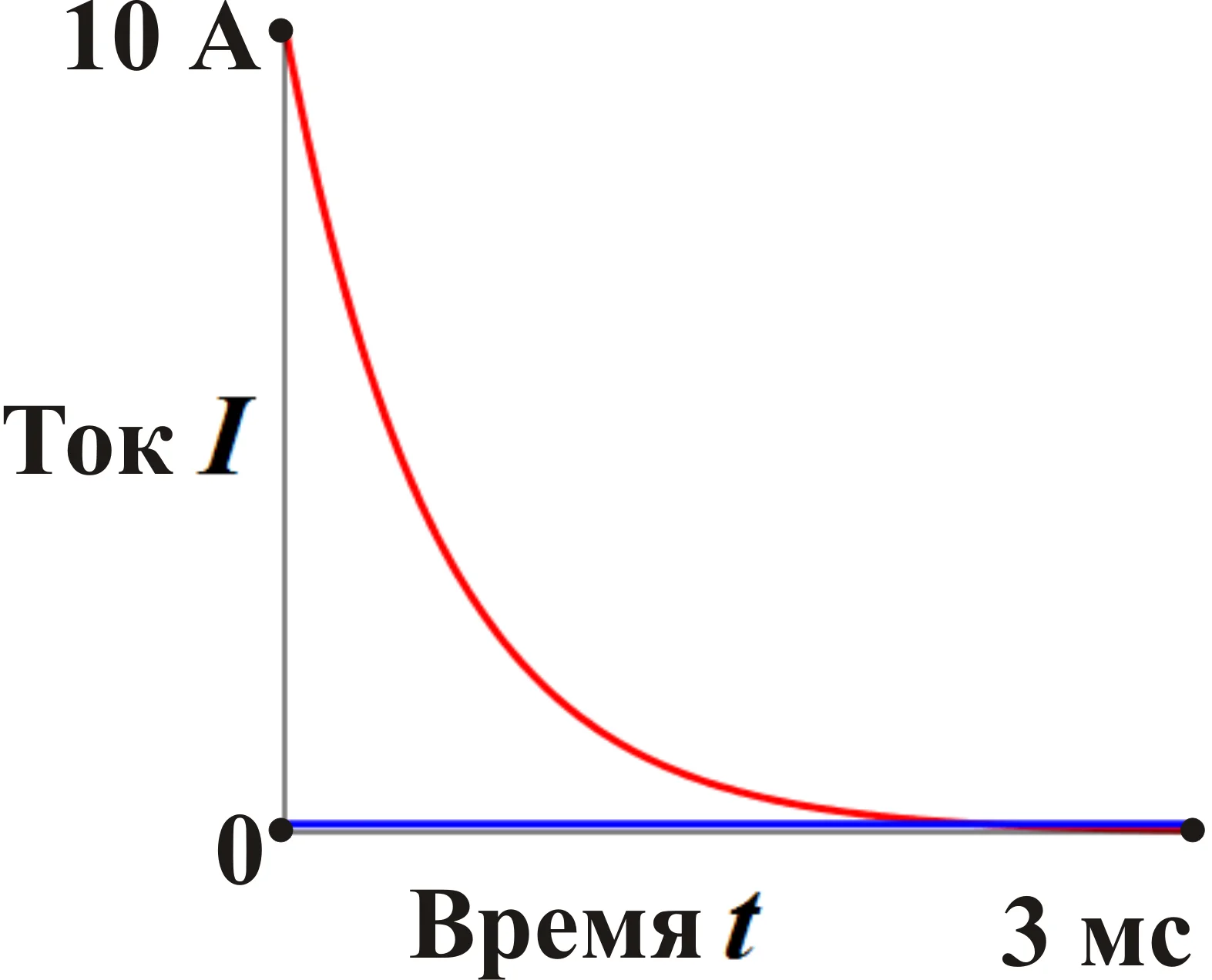    Задача 6 Задача 7 Задача 8 Задача 9  Тема 3 задача 1 По закону Кулона F=E*q q - точечный заряд, Кл; E - напряженность в точке (см. рисунок) Складываем вектора E и E1+E2 По теореме Пифагора: E= где, E1=q/4piE0r^2 E2+E3=2q'tg(a)^2/4piE0(r)^2=2q'/4piE0(r)^2 r - расстояние между диполем и зарядом (перпендикуляр), E0 - электрическая постоянная = 8,85*10^(-12) Ф/м; pi = 3,14, q1=q2=q'- заряд частиц (т.к. электрический диполь - система из 2х равных по величине зарядов); a - угол p=q'l (формула дипольного момента). Отсюда находим q' = p/l и поставляем в первую формулу. l=2*r/tg(a) - расстояние между зарядами в диполе. Задача 2 Задача 3  Задача 4  Тема 4 задача1 Задача 2  Задача3 Задача №8.3.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ» Дано: S=5 см2, B=0,5 Тл, Mmax=0,25 мН·м, I−? Решение задачи: Если в однородное магнитное поле внести рамку (или плоский контур, что то же самое), по которой течет ток, то в общем случае на стороны рамки будут действовать силы Ампера. Эти силы создадут вращающий момент сил M, который можно найти по следующей формуле: M=BISsinα В этой формуле B – индукция магнитного поля, I – сила текущего в рамке (контуре) тока, S – площадь рамки (контура), α – угол между нормалью к плоскости контура и вектором магнитной индукции. Очевидно, что максимальный магнитный момент будет наблюдаться тогда, когда угол α между нормалью к плоскости контура и вектором магнитной индукции будет равен 90°, то есть плоскость контура будет параллельна линиям магнитной индукции (смотрите рисунок к задаче). Поэтому: Mmax=BIS Откуда искомая сила I равна: I=Mmax/BS Задача решена в общем, подставим данные задачи в формулу, переведя их в систему СИ, и посчитаем ответ: I=0,25⋅10–3/0,5⋅5⋅10–4=1А Ответ: 1 А. Задача4  Задача5 Задача6  Задача7 Дано: Δt=5 мс, N=500, Φ1=7 мВб, Φ2=3 мВб, Ei−? Решение задачи: Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока. Поэтому: Ei=ΔΦ/Δt(1) Следует отметить, что для определения мгновенного значения ЭДС индукции по этой формуле интервал времени Δt должен стремиться к нулю, в противном случае Вы получите среднее значение ЭДС индукции. Будем считать, что в нашем случае магнитный поток изменялся равномерно, поэтому интервал времени Δt может быть каким угодно – среднее и мгновенное значения ЭДС индукции в таком случае будут одинаков Также учтем, что соленоид имеет N витков, тогда формула (1) запишется в таком виде: Ei=NΔΦ/Δt(2) Понятно, что модуль изменения магнитного потока ΔΦ равен разности потоков Φ1 и Φ2: ΔΦ=Φ1–Φ2 С учётом этого выражения, формула (2) примет вид: Ei=N(Φ1–Φ2)/Δt Задача решена в общем виде, подставим данные задачи в полученную формулу и произведем расчёт численного ответа: Ei=500⋅(7⋅10–3–3⋅10–3)/5⋅10–3=400В=0,4кВ Ответ: 0,4 кВ. Задача8 Ответ: 21,8 Ом. |
