Решение дифференциальных уравнений
 Скачать 125.5 Kb. Скачать 125.5 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра РАПС отчет по лабораторной работе №9 по дисциплине «Информатика» Тема: Решение дифференциальных уравнений
Санкт-Петербург 2022 Цель работы. Изучение возможностей, предоставляемых MatLab, для численного решения обыкновенных дифференциальных уравнений произвольного порядка и систем с начальными условиями, т. е. задачи Коши. Основные теоретические положения. Функциями решения дифференциальных уравнений являются ode23(), ode45() и другие, имеющие вид: [t, x] = ode23('fun', t0, tf, x0) [t, x] = ode45('fun', t0, tf, x0) [t, x] = ode23('fun', t0.tf.x0, tol, trace) [t, x] = ode45('fun', t0.tf.x0, tol, trace) где: 'fun' – имя m-файла, в котором содержатся правые части системы дифференциальных уравнений; t0 – начальное значение аргумента; tf – конечное значение аргумента; х0 – вектор начальных условий; tol – задаваемая точность решения дифференциальных уравнений; trace – выдача промежуточных результатов. Схема решения задач с начальными условиями Задача Коши для дифференциального уравнения состоит в нахождении функции, удовлетворяющей дифференциальному уравнению произвольного порядка y(n) = f(t, y, y′, …, y(n– 1) и начальным условиям при t= t0 y(t0) = u0, y′(t0) = u1, …, y(n– 1)(t0) = un– 1. Схема решения состоит из следующих этапов: 1. Приведение дифференциального уравнения к системе дифференциальных уравнений первого порядка. 2. Написание специальной файл - функции для системы уравнений. 3. Вызов подходящего солвера. 4. Визуализация результата. Пример 1 Уравнение, описывающее движение, имеет вид y′′ + 2·y′ + 10·y = sin t. 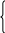  =  у1′ = y2 ; у1(0) 0 у1′ = y2 ; у1(0) 0 у2′ = –2·y2 – 10·yl + sin t у2(0) 1 . F= @[y(2); –2*y(2) – 10*y(l) + sin(t)]; % формирование вектора начальных условий »Y0 = [1; 0]; % вызов солвера от файл-функции diff1, начального и конечного % момента времени и вектора начальных условий »[Т, Y] = ode45('F', [0 15], Y0) ; % вывод графика решения исходного дифференциального уравнения »plot(T, Y(:, l), 'r') % вывод графика производной от решения исходного % дифференциального уравнения »hold on »plot(T, Y(:, 2), 'k--') %вывод пояснений на график »title(' Solve {\ity} \prime\prime+2{\ity} \prime+10{\ity} = sin{\itt}') »xlabel('\itt') »ylabel('{\ity}, {\ity} \prime ') »legend('coordinates', 'speed') »grid on »hold off 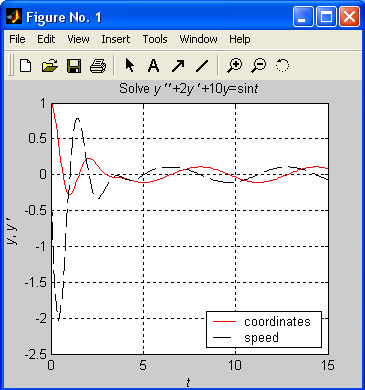 Из графика видно, что приближенное решение и его производная удовлетворяют начальным условиям, колебание происходит в установившемся режиме, начиная с t = 5. Пример 2. Решите систему дифференциальных уравнений у 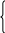 1′ = y2 ; 1′ = y2 ;у2′ = –1/t2 на отрезке [а, 100] при начальных условиях у1(а) = ln а, у2(а) = 1/а,взяв а = 0.001. Легко проверить, что точным решением этой системы является у1= ln t, у2 = 1/t.Надо уменьшить относительную погрешность вычислений при помощи формирования options с использованием odeset и включении options дополнительным четвертым аргументом в солвер. Для задания относительной погрешности служит аргумент ' RelTol ', например options = odeset(' RelTol ', 1.0е–04) Только точность 10–6 обеспечивает получение приближенного решения, график которого почти совпадает с графиком точного решения. »а = 0.001; f=@(t,y)[y(2);-1/t.^2]; % задание начальных условий »Y0 = [log (а); 1/а]; % вызов солвера ode45 при различных погрешностях %и вывод графиков приближенных решений % точность 0.001 »options = odeset('RelTol', 1.0e–3); »[T, Y] = ode45(f, [a 100], Y0, options); »plot(T, Y(:, 1), 'k:') % точность 0.0001 »options = odeset('RelTol', 1.0e–4); »[T, Y] = ode45(f, [a 100], Y0, options); »hold on »plot(T, Y(:, 1), 'k--') % точность 0.000001 »options = odeset('RelTol', 1.0e–6); »[T, Y] = ode45('f', [a 100], Y0, options); »hold on »plot(T, Y(:, 1), 'k-') % вывод графика точного решения »t = [a:4:100]; »у = log(t) ; »hold on »plot(t, y, 'ko') % нанесение информации на график »xlabel('\itt') »ylabel('\ity') »title('Comparison of the decision at various errors') »legend('10^{-3}', '10^{-4}', '10^{-6}', 'The exact decision',) »grid on »hold off Ход работы. Пример 1: >> F=@(t,y)[y(2);-2*y(2)-10*y(1)+sin(t)]; >> % формирование вектора начальных условий >> Y0=[1;0]; >> % вызов солвера от файл-функции diff1, начального и конечного >> % момента времени и вектора начальных условий >> [T, Y] = ode45(F, [0 15], Y0) ; >> % вывод графика производной от решения исходного >> plot(T, Y(:, 1), 'r') >> % вывод графика производной от решения исходного >> % дифференциального уравнения >> hold on >> plot(T, Y(:, 2), 'k--') >> % вывод пояснений на график >> title(' Solve {\ity} \prime\prime+2{\ity} \prime+10{\ity} = sin{\itt}') >> xlabel('\itt') >> ylabel('{\ity}, {\ity} \prime ') >> legend('coordinates', 'speed') >> grid on >> hold off  Пример 2: >> a = 0.001; >> f=@(t,y)[y(2);-1/t.^2]; >> % задание начальных условий >> Y0 = [log (a); 1/a]; Error using log Not enough input arguments. >> Y0 = [log(a); 1/a]; >> % вызов солвера ode45 при различных погрешностях >> % и вывод графиков приближенных решений >> % точность 0.001 >> options = odeset('RelTol', 1.0e-3); >> [T, Y] = ode45(f, [a 100], Y0, options); >> plot(T, Y(:, 1), 'k:') >> % точность 0.0001 >> options = odeset('RelTol', 1.0e-4); >> [T, Y] = ode45(f, [a 100], Y0, options); >> hold on >> plot(T, Y(:, 1), 'k--') >> % точность 0.000001 >> options = odeset('RelTol', 1.0e-6); >> [T, Y] = ode45(f, [a 100], Y0, options); >> hold on >> plot(T, Y(:, 1), 'k-') >> % вывод графика точного решения >> t = [a:4:100]; >> y = log(t) ; >> hold on >> plot(t, y, 'ko') >> % нанесение информации на график >> xlabel('\itt') >> ylabel('\ity') >> title('Comparison of the decision at various errors') >> legend('10^{-3}', '10^{-4}', '10^{-6}', 'The exact decision') >> grid on >> hold off 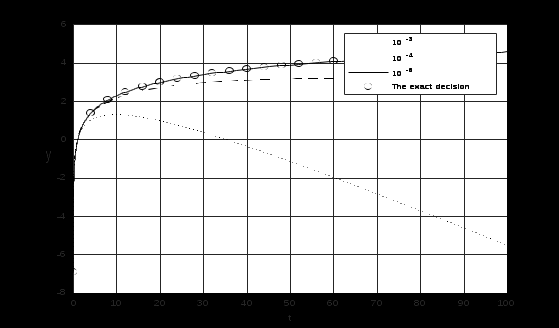 Вывод. Численные решения обыкновенных дифференциальных уравнений произвольного порядка и систем с начальными условиями, т. е. задачи Коши-с ними MatLab способен справиться и показать всё наглядно. |
