практическая математика. Решение Если принять y k, то уравнение изоклины для заданного уравнения k 2

• Название: Решение Если принять y k, то уравнение изоклины для заданного уравнения k 2
• Анкор: ghfrnbxtcrfz
• Дата: 22.05.2023
• Размер: 318.93 Kb.
• Имя файла: практическая математика.docx
• Тип: Решение; #1150633

1. Методом изоклин построить интегральные кривые уравнения

1.1.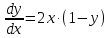

Решение

Если принять y’=k, то уравнение изоклины для заданного уравнения:

k=2x(1-y) или y=1-(k/2x) – уравнение гипербол.

Для примера ограничимся значениями: k₁=1, k₂=2, k₃=10.

Построим интегральные кривые, пересекающие каждую из гипербол-изоклин под определённым углом: первую под углом, определяемым угловым коэффициентом k₁ , вторую под углом, определяемым угловым коэффициентом k₂ и третью под углом, определяемым угловым коэффициентом k₃.

Сделаем чертеж: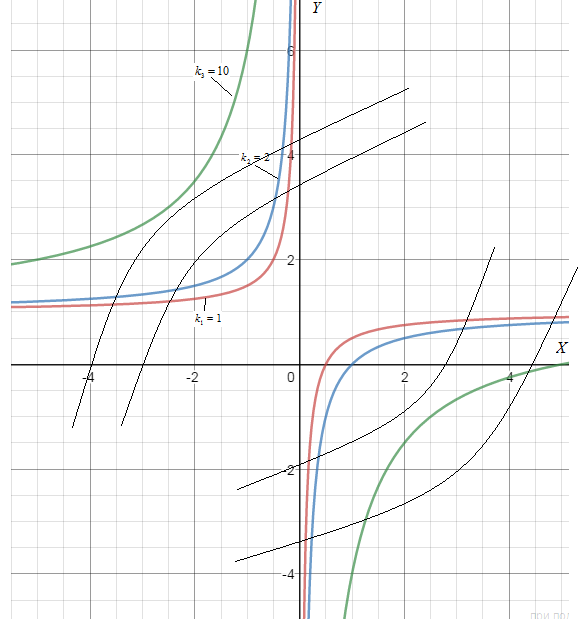



Ответ: на рисунке показаны интегральные кривые.

2. Решить уравнение, допускающее понижения порядка

2.1.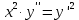

Решение

Замена: P=y’ , тогда P’=y’’ , где P - некоторая функция от x.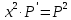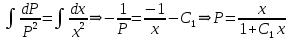





Найдем y :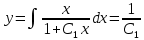



,

- некоторые постоянные.

3. Решить систему уравнений

3.1.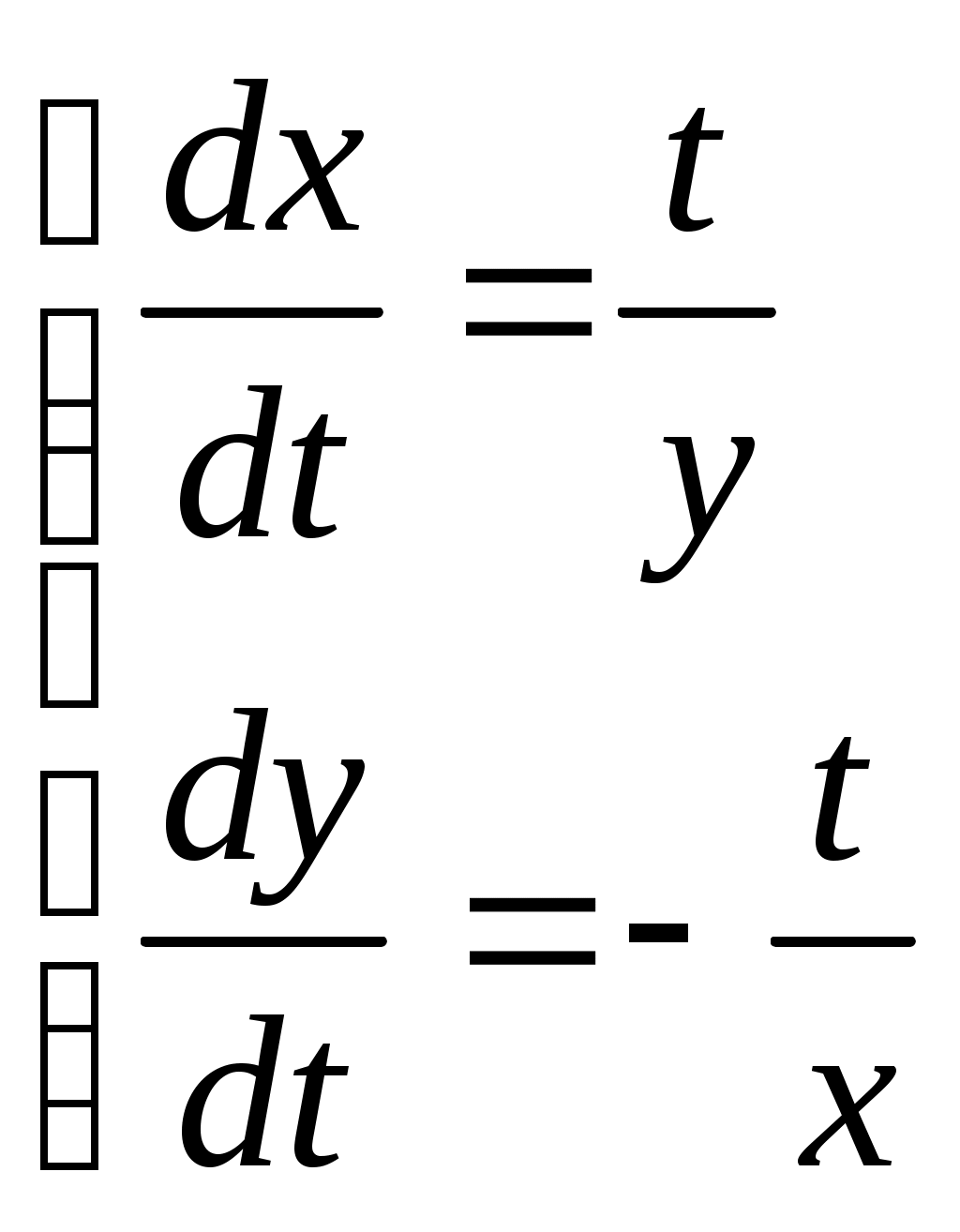

Решение

Имеем 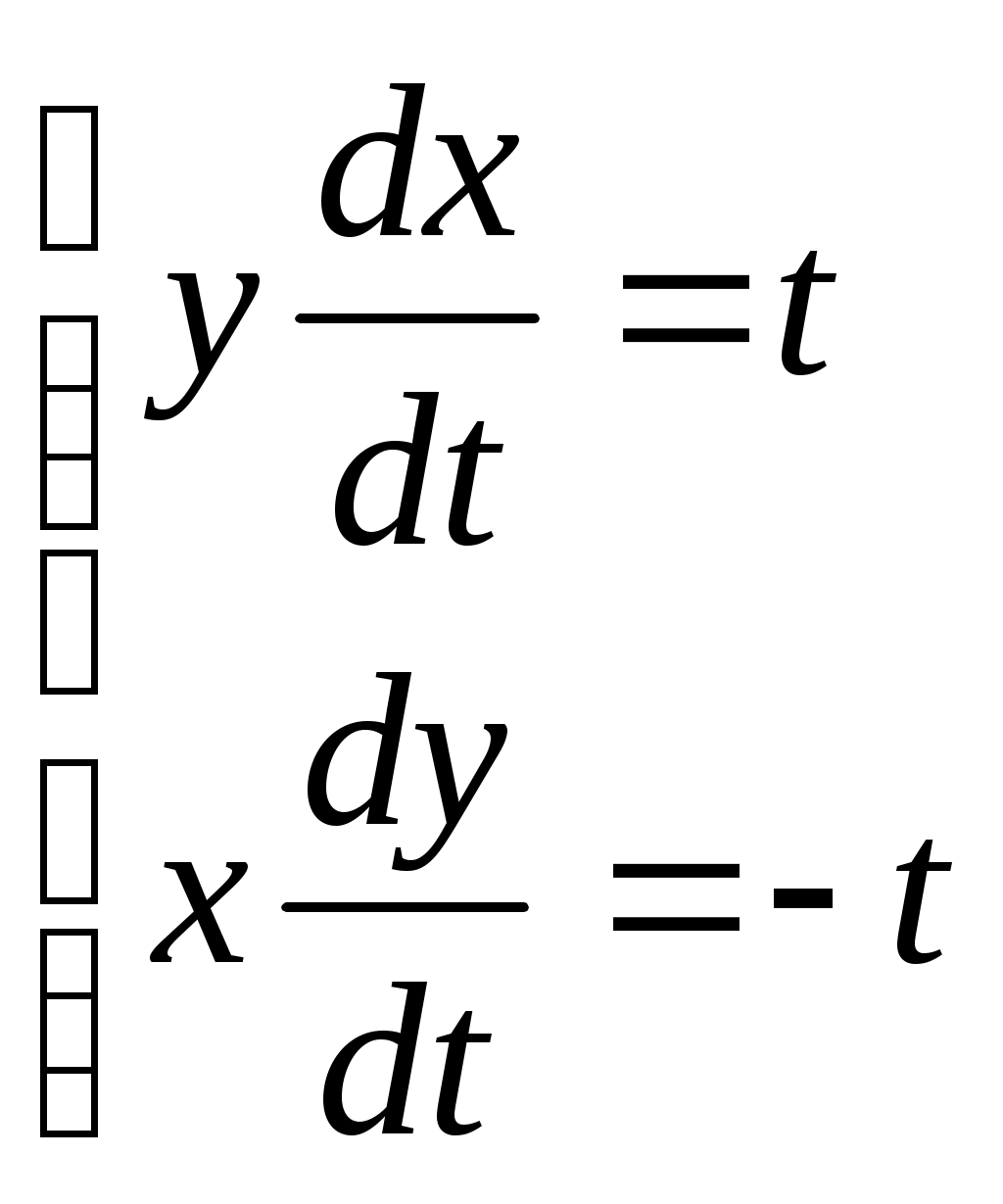, складываем оба уравнения: .

или .

Следовательно, . Делаем 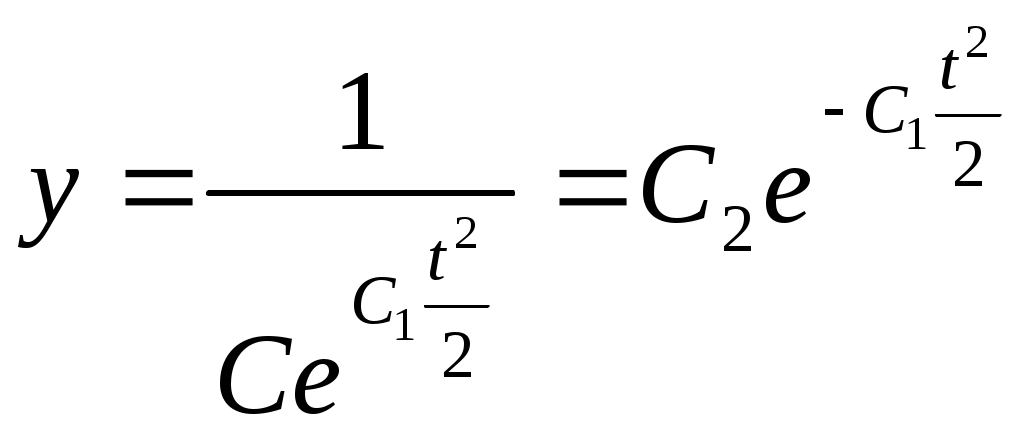подстановку в первое уравнение системы.

или .

Найдем : .

В итоге: 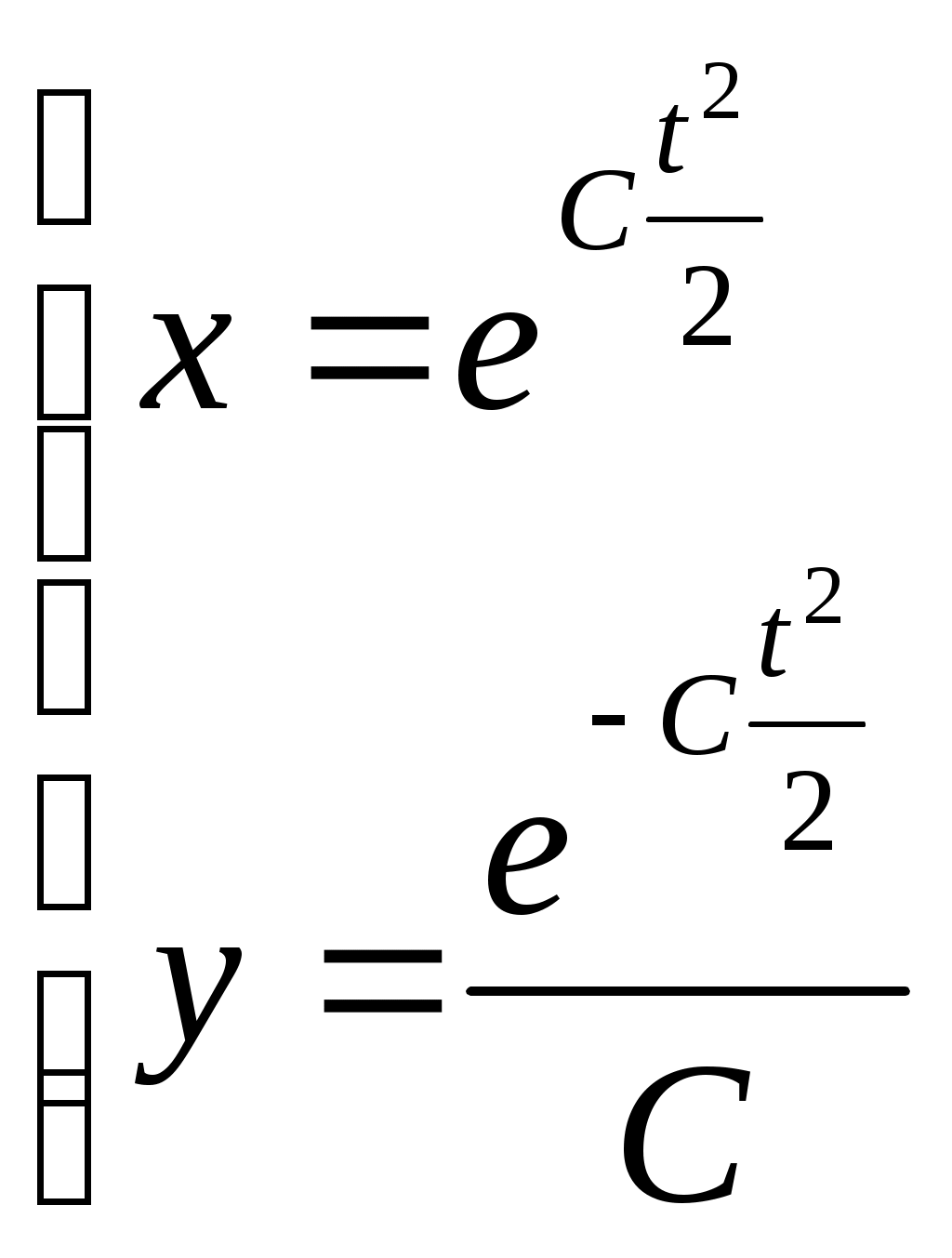, - некоторые постоянные.

Ответ: .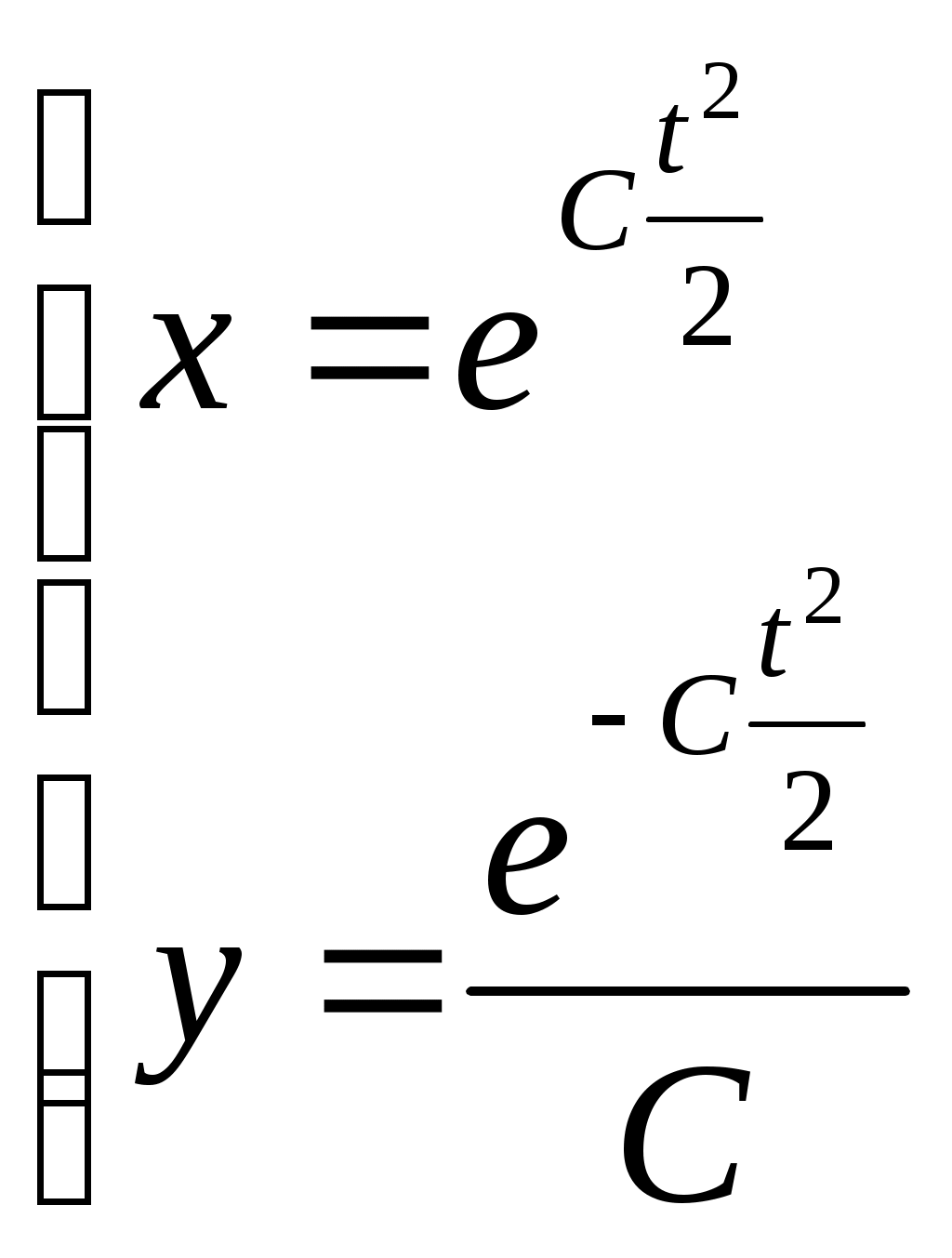

4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?

Решение

Наивероятнейшее число k₀ определяют из двойного неравенства , причем:

1) если число np – q дробное, то существует одно наивероятнейшее число k₀;

2) если число np – q целое, то существует два наивероятнейших числа, а именно: k₀ и k₀ + 1;

3) если число np целое, то наивероятнейшее число k₀ = np.

пусть провели испыт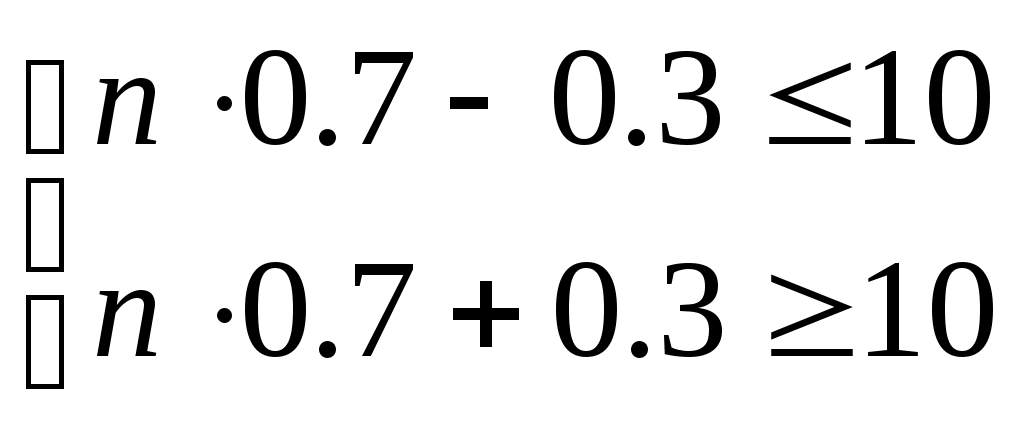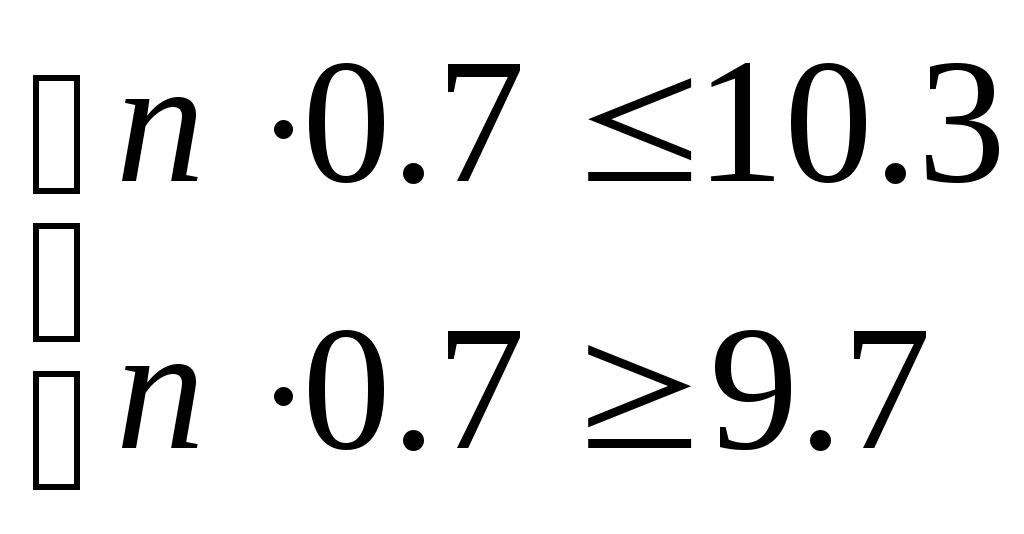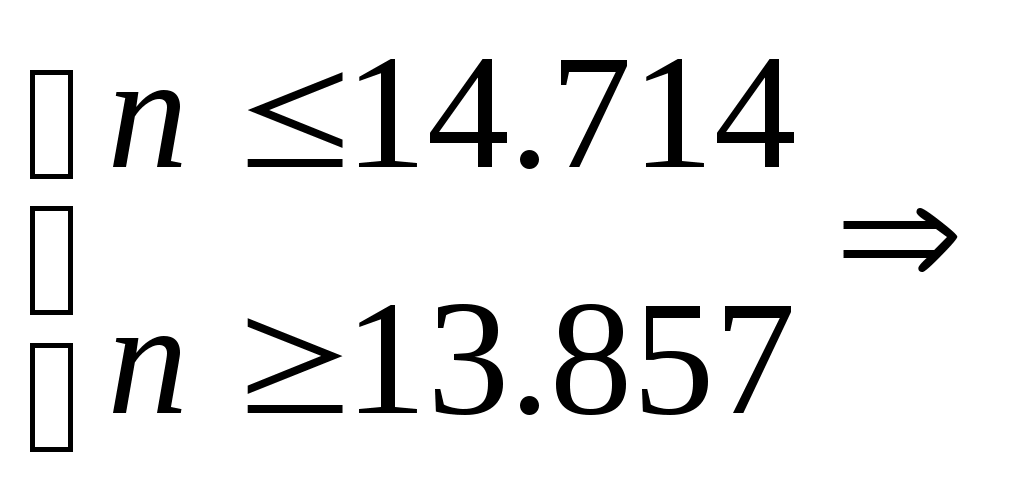аний.

Имеем:







.

Ответ: .