Лабораторная работа 1,2,3. Решение. Определим параметр Коши по формуле 12) Давление столба жидкости над плунжером

• Название: Решение. Определим параметр Коши по формуле 12) Давление столба жидкости над плунжером
• Дата: 29.05.2022
• Размер: 94.3 Kb.
• Имя файла: Лабораторная работа 1,2,3.docx
• Тип: Решение; #555787

Лабораторная работа 1

Определить длину хода плунжера по статической теории.

Исходные данные: диаметр плунжера Dпл = 43 мм, диаметр насосных штанг d = 22 мм, диаметр НКТ dт = 73 х 5,5 мм, глубина спуска насоса L = 1500 м, длина хода сальникого штока S = 2,1 м, динамический уровень hд = 1450 м, число качаний в минуту n = 9, плотность жидкости ρж =900 кг/м³, сила сопротивления движению плунжера Рс = 9 кН, буферное давление в выкидной линии - 1,0 МПа, кинематическая вязкость нефти ν = 0,1 см²/с при 80°С.

Решение. Определим параметр Коши по формуле (2.12):

.

Давление столба жидкости над плунжером



Потери давления за счет сопротивления потоку жидкости в трубах определим по соотношению

,

где средняя скорость в подъемных трубах



Число Рейнольдса

.

Коэффициент гидравлического сопротивления

.

.

Давление под плунжером (сопротивлением клапанов пренебрегаем)

.

Тогда вес столба жидкости над плунжером (формула (2.27))

.

Удлинение штанг (формула (2.26))

,

где площадь поперечного сечения штанг

.

Удлинение труб при ходе штанг вниз (формула (2.28))

,



Деформация штанг за счет силы сопротивления при ходе штанг вниз (формула (2.25))



Потери хода за счет изгиба штанг определим по формуле (2.32), так как Рс < 10 кН. Предварительно определим:



Осевой момент инерции для штанг

.

.

Длина хода плунжера при действии статических сил Pпл

.

Задача 11. Определить длину хода плунжера по статической и динамической теориям.

Исходные данные: диаметр плунжера Dпл = 43 мм, диаметр насосных штанг dш = 22 мм, диаметр НКТ - dт = 73 x 5,5 мм, глубина спуска насоса L = 1500 м, длина хода сальникого што­ка S = 2,1 м, динамический уровень hд = 1450 м, число качаний в минуту n = 15, плотность жидкости ρж = 900 кг/м³, сила сопротивления движению плунжера Рс = 4 кН, буферное давление в выкидной линии - 1,0 МПа, кинематическая вязкость нефти ν = 0,1 см²/с при 80°С.

Решение. Определим параметр Коши по формуле (2.12):





Следовательно, режим откачки находится в области динамических режимов.

Определим среднюю скорость в подъемных трубах:



Число Рейнольдса

.

Коэффициент гидравлического сопротивления

.

Потери давления за счет сопротивления потоку жидкости в трубах определим по соотношению



.

Вес столба жидкости над плунжером (формула (2.27))

.

Удлинение штанг (формула (2.26))

.

Удлинение труб при ходе штанг вниз (формула (2.28))

,



Сжатие штанг за счет силы сопротивления при ходе штанг вниз (формула (2.29))

.

Потери хода за счет изгиба штанг определим по формуле (2.32), так как Рс < 10 кН. Предварительно определим:





Длина хода плунжера при действии статических сил

.

Так как колонна штанг одноступенчатая, а жидкость вязкая, то за расчетную формулу выбираем (2.35). Определим параметр β1, выбирая b = 0,6:





Параметр μ в градусах



Длина хода плунжера по формуле (2.35)

Лабораторная работа 2

Задача 13

Выбрать и рассчитать на прочность одноступенчатую колонну штанг для СК согласно варианту в журнале.

Дано:

глубина спуска насоса	м	800
динамический уровень	м	780
буферное давление	МПа	0,5
диаметр плунжера D	мм	40
диаметр штанг dш	мм	22
плотность жидкости  ρж	кг/м3	870

Решение

Выберем предварительно штанги диаметром мм и определим параметр Коши: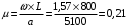

, (1)

где: а - скорость звука в штангах = 5100 м/с;

ω - угловая скорость в 1/с, ω = π·n / 30;

Режим статический (динамический).

Определим перепад давления над плунжером из формулы: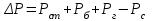

(2)

Полагаем, что гидравлическое сопротивление движению жидкости в трубах мало (Рг = 0). Найдем статическое давление над плунжером:

, Н/м² (МПа) (3)

Давление под плунжером

, Н/м² (МПа) (4)

Перепад давления над плунжером

МПа

Кинематический показатель совершенства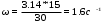

;



Амплитуда напряжения цикла по формуле(2.35)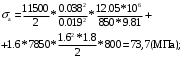



Среднее напряжение в штангах по формуле (2.17)



по формуле (2.18)



Максимальное напряжение



Приведенное напряжение



Допустимы штанги из ст.40 =120 МПа.

Нормализация с поверхностным упрочнением ТВЧ 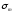=320 МПа.

Задача 16

Лабораторная работа 3

Дано: глубина подвески насоса L = 1870 м, динамический уровень hд = 1800м, Dпл = 32 мм, dтр = 60мм, диаметры штанг: dш1 = 22 мм, L1 = 560 м (30%); dш2 = 19 мм, L2 = 1310 м (70%); плотность жидкости ρж = 880 кг/м³, станок-качалка СК-12-2,5-4000.

Решение. По формуле (2.12) определим параметр Коши, а = 4900 м/с; α = 1,26 с-1;

.

Режим динамический, следовательно, формулы динамической теории дадут наиболее правильную нагрузку.

1. 
   1.       Статическая теория, формулы (2.13), (2.17).
   

По формуле (2.14) определим Рж, учитывая, что Рб = 0:

;

.

Для СК-12 S_А = 2,5 м, nmax = 12 мин^-1. Тогда

.

Вес штанг в воздухе

;

;

.

2. 
   2.       Формулы А. С. Вирновского (2.18) - (2.20).
   

;

;

;

.

Тогда

;

;

;

;

;

.

Для С К-12-2,5- 4000 при S_А = 2,5 м [15]

.

Исходя из вычисленных коэффициентов по формуле (2.18)



 

По формуле (2.19)

3. 
   3.       Упрощенные формулы А. С. Вирновского (2.21)
   

;

.

4. 
   4.       Формула И. А. Чарного
   

;

;



5. Формула А. Н. Адонина

;



Таким образом, принимая за основу нагрузку, рассчитанную по формулам А. С. Вирновского, можно сказать, что наиболее близкие значения по Рmax дают формулы А. Н. Адонина (+809) и упрощенная формула А. С. Вирновского ( - 3428); по Рmin наиболее близкие значения дают упрощенная формула А. С. Вирновского (+2400 Н) и формула И. М. Муравьева (+3670 Н).