математика. Практические задачи математика— копия. Решение Положим, тогда,

• Название: Решение Положим, тогда,
• Анкор: математика
• Дата: 18.02.2022
• Размер: 133.5 Kb.
• Имя файла: Практические задачи математика— копия.doc
• Тип: Документы; #366075

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» Кафедра экономики и управления Форма обучения: заочная/очно-заочная
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКЕ
Группа Пм20ГУ191
Студент		Елена Александровна Алимова

МОСКВА 2022

1. Методом изоклин построить интегральные кривые уравнения

1.1.
Решение:

Положим , тогда ,  .

Если k=0, то получаем прямую 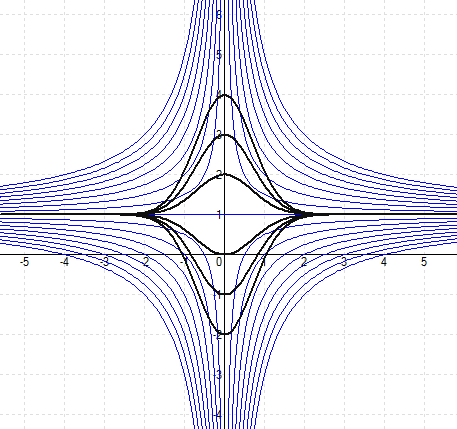, т.е. экстремумы функции находятся на прямой . Построим семейство изоклин.



2. Решить уравнение, допускающее понижения порядка

2.1.
Решение:

Пусть , тогда . Подставим эти выражения в исходное уравнение:













3. Решить систему уравнений

3.1.
Решение:













Пусть , тогда . Подставим эти выражения в уравнение:



















4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?
Решение:

Наивероятнейшее число появления события задается неравенством: .

По условию p=0,7, q=1-p=1-0,7=0,3, k₀=10. Подставим известные данные в неравенство:





Поскольку n целое, то n=14. Т.е. нужно провести 14 испытаний.