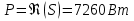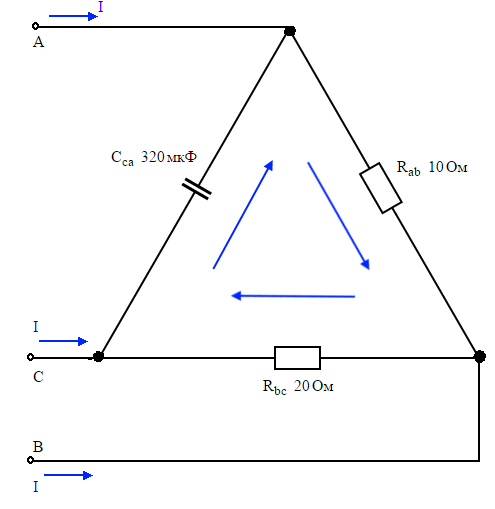
Задача 2. Решение. Составим расчетную схему цепи, с указанием номиналов элементов и условноположительных направлений токов

• Название: Решение. Составим расчетную схему цепи, с указанием номиналов элементов и условноположительных направлений токов
• Дата: 16.01.2019
• Размер: 131.29 Kb.
• Имя файла: Задача 2.docx
• Тип: Решение; #63923

Вариант 23

В трехфазную сеть включили «треугольником» несимметричную нагрузку: в фазу АВ резистивный элемент R_АВ = 10 Ом , в фазу ВС – резистор с сопротивлением R_BC = 20 Ом; в фазу СА – емкостной элемент с емкостью Сса = 320 мкФ.
Линейное напряжение Uном = 220 В, частота сети f = 50 Гц. 
Определить фазные токи I_AB , I_BC, I_CA , активную, реактивную и полную мощности трехфазной цепи. 
Расчетное значение Xс округлить до целого числа. 
Построить векторную диаграмму и по ней определить линейные токи I_A, I_В, I_С



Решение.

Составим расчетную схему цепи, с указанием номиналов элементов и условно-положительных направлений токов



Предполагая источник напряжения стандартным, найдем фазы питающего напряжения:

UAB = 220, В

UBC = (220) × e-j120 = -110-j190.526, В

UCA = (220) × ej120 = -110+j190.526, В

Циклическая частота сети:

ω = 2πf = 2π × (50) = 314.159

Сопротивления в комплексной форме:

Xca	=	1	=	1	= -j10, Ом
		ωCca		(314.159) × (320 × 10-6)

ZAB = Rab = (10) = 10, Ом

ZBC = Rbc = (20) = 20, Ом

ZCA = Xca = -j10, Ом

Фазные токи:

IAB	=	UAB	=	(220)	= 22, А
		ZAB		(10)

IBC	=	UBC	=	(-110-j190.526)	= -5.500-j9.526, А
		ZBC		(20)

ICA	=	UCA	=	(-110+j190.526)	= -19.053-j11, А
		ZCA		(-j10)

Модули фазных токов:

|IAB| = √(Re2+Im2) = √(222 + 02) = 22, А

|IBC| = √(Re2+Im2) = √((-5.5)2 + (-9.526)2) = 11, А

|ICA| = √(Re2+Im2) = √((-19.053)2 + (-11)2) = 22, А

Полная мощность, потребляемая в фазах:

SAB = PAB + QAB  = |IAB|2 (Rab) = (22)2 × (10) = 4840, ВА

SBC = PBC + QBC  = |IBC|2 (Rbc) = (11)2 × (20) = 2420, ВА

SCA = PCA + QCA = |ICA|2 (XCca) = (22)2 × (-j10) = -j4840, ВА

Общая мощность, потребляемая нагрузкой, равна сумме мощностей фаз:

Sн = SAB + SBC + SCA = (4840) + (2420) + (-j4840) = 7260-j4840, ВА

При этом действительная часть полной мощности представляет из себя активную мощность, а мнимая часть – реактивную:





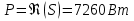
Векторная диаграмма фазных токов:



Определим линейные токи как разность или сумма соответствующих фазных токов, согласно первому закону Кирхгофа:

IA = IAB - ICA

IB = IBC - IAB

IC = ICA - IBC

Измерив величины векторов по диаграмме, получаем:

I_A = 41+j11, A

I_B = -27-j9, A

I_C = -13+j1, A
Проверим найденные значения аналитически:

IA = IAB - ICA  = (22)- (-19.053-j11) = 41.053+j11, А

IB = IBC -IAB = (-5.500-j9.526)- (22) = -27.500-j9.526, А

IC = ICA - IBC = (-19.053-j11) -(-5.500-j9.526) = -13.553-j1.474, А