Решение Вычисляем степень статической неопределимости балки
 Скачать 0.93 Mb.
|
|
Задача 1 Для заданной статически неопределимой стальной балки требуется: 1) раскрыть статическую неопределимость; 2) построить эпюру изгибающих моментов; 3) подобрать двутавровое сечение по условию прочности балки; 4) определить угол поворота сечения L и прогиб в сечении К. Дано: Р = 7 кН; Р1 = 6 кН; а = 1 м; R = 160 МПа; E = 2·105 МПа 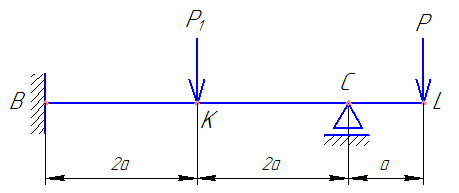 Решение: 1. Вычисляем степень статической неопределимости балки. По условиям закрепления имеем четыре опорных реакции: три на опоре В и одну на опоре С. Для плоской системы сил можно составить только три уравнения равновесия, поэтому степень статической неопределимости балки n = 4 – 3 = 1, т.е. система один раз статически неопределима. Выбор основной системы. Основная система (ОС) получается из заданной (ЗС) отбрасыванием «лишних» связей и заменой их неизвестными обобщенными силами. ОС должна быть геометрически неизменяемой и статически определимой. Отбросим связь в опоре С. Соответствующая обобщенная реакция – Х1. Получаем эквивалентную систему. Построим эпюры от действия единичной нагрузки Х1 и внешней нагрузки. Запишем каноническое уравнение метода сил.  δ11 – перемещение в ОС по направлению Х1 от действия единичной нагрузки Х1; Δ1Р – перемещение от внешней нагрузки.   – изгибающий момент от единичной нагрузки Х1.  – изгибающий момент от внешней нагрузки.Определим коэффициенты канонических уравнений путем перемножения единичных и грузовых эпюр.   Подставим найденные значения коэффициентов в каноническое уравнение и решим его.   2. Построение эпюры M. Окончательная эпюра M строится с использованием принципа суперпозиции.   Эпюру М строим по суммарным значениям  в характерных сечениях.Выполним деформационную проверку. Для проверки правильности расчётов и построения эпюры изгибающих моментов используем условие равенства нулю угла поворота смежных сечений балки над опорой С (перемещение по направлению отброшенной связи). Этот угол вычисляется перемножением эпюры моментов от единичной нагрузки и окончательной эпюры изгибающих моментов. 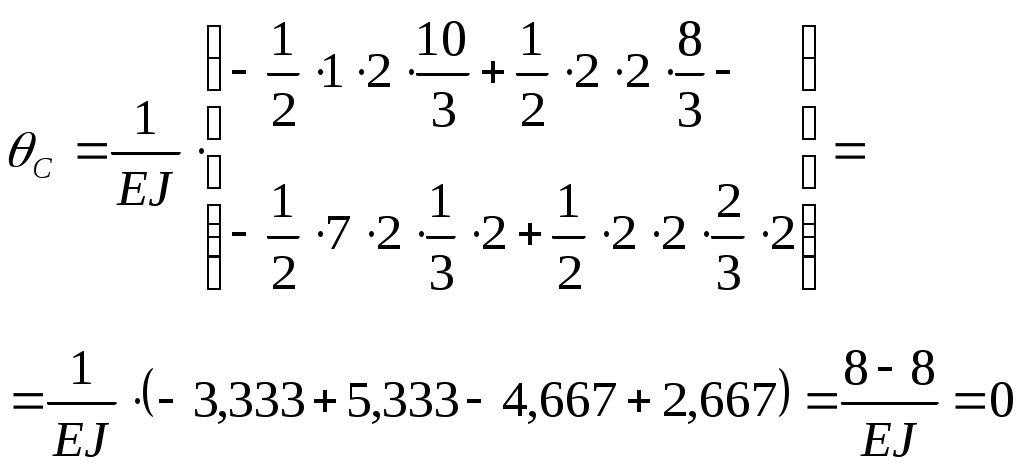 Деформационная проверка выполняется. Расчеты проведены верно. 3. Расчет на прочность. Запишем условие прочности   Опасное сечение С, где действует максимальный изгибающий момент.  Определим требуемый момент сопротивления сечения  По сортаменту выбираем двутавр №12 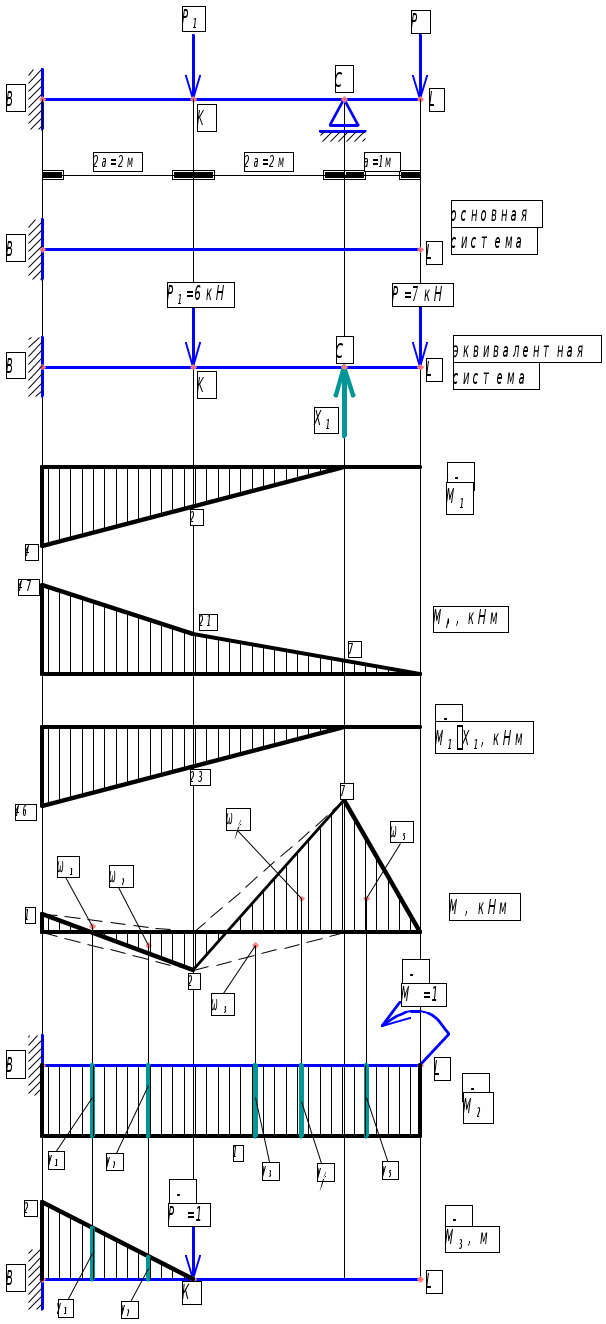 ,   4. Определим угол поворота сечения L и прогиб в сечении К. Определим угол поворота в сечении L. Приложим в этом сечении единичный момент  . Построим эпюру моментов от единичной нагрузки  . Для определения угла поворота в сечении L воспользуемся интегралом Мора, который вычислим методом Верещагина. ωi– площадь грузовой эпюры yi– значение на единичной эпюре под центром тяжести ωi Разобьем грузовую эпюру на простые фигуры и определим площади фигур и ординаты их центров тяжести на единичной эпюре.           Определим угол поворота в сечении L: 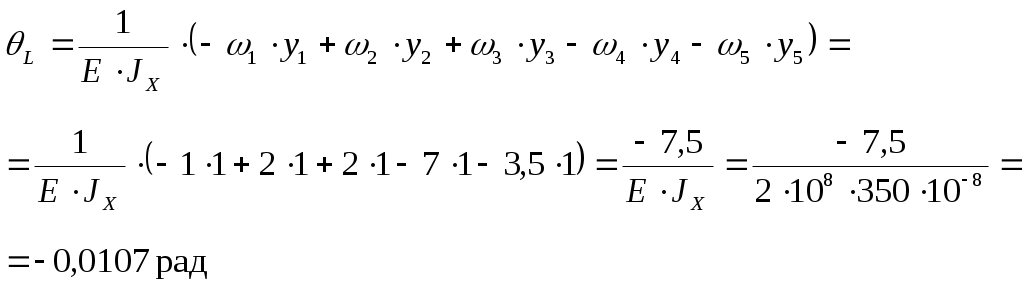 Отрицательный знак угла поворота говорит о том, что точка L повернется против направления заданного момента  , т.е. по часовой стрелке.Определим прогиб в сечении K. Приложим в этом сечении единичную силу  по направлению искомого перемещения. Построим эпюру моментов от единичной нагрузки  . Для определения прогиба в сечении К воспользуемся интегралом Мора, который вычислим методом Верещагина. Разобьем грузовую эпюру на простые фигуры и определим площади фигур и ординаты их центров тяжести на единичной эпюре.   Определим прогиб в сечении K:  Задача 2 Стальной валделает n оборотов в минуту и передает мощность N, кВт. Требуется подобрать диаметр вала из условия его прочности при совместном действии изгиба и кручения. Дано: n = 120 об/мин; N = 12 кВт; D1 = 0,2 м; D2 = 0,6 м; а = 0,4 м; b = 0,3 м; с = 0,3 м; n = 3; сталь 45 схема 2 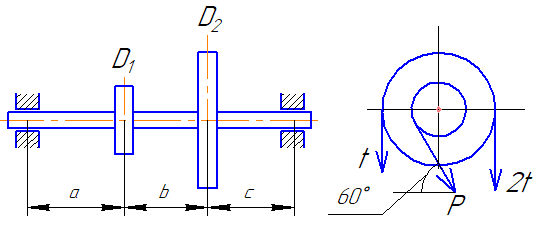 Решение: Определим вращающий момент, передаваемый ведущим валом:  Строим эпюру крутящих моментов. Найдем окружные усилия на шкивах. 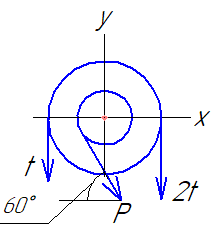   Найдем проекции сил    Определим изгибающие моменты в характерных сечениях. – горизонтальная плоскость Составим расчетную схему, определим реакции в подшипниках.  ;    ;   Проверка:  Опорные реакции найдены верно. Определим изгибающие моменты в характерных сечениях.   Н∙м Н∙м Строим эпюру изгибающих моментов MГОР. – вертикальная плоскость Составим расчетную схему, определим реакции в подшипниках. ;   ;   Проверка:  Опорные реакции найдены верно. Определим изгибающие моменты в характерных сечениях.   Н∙м Н∙м Строим эпюру изгибающих моментов MВЕРТ. Определим эквивалентные моменты в характерных сечениях вала.      Опасным является сечение C. Определим диаметр вала, используя условие прочности.     преде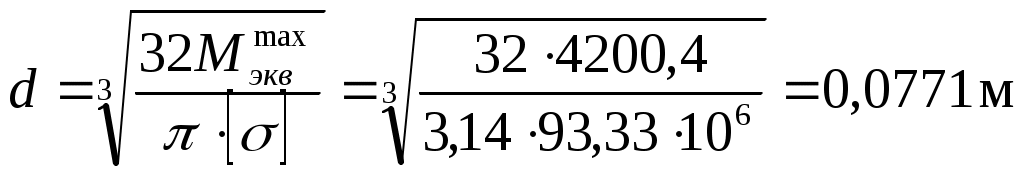л текучести для стали 45 Тогда  Принимаем 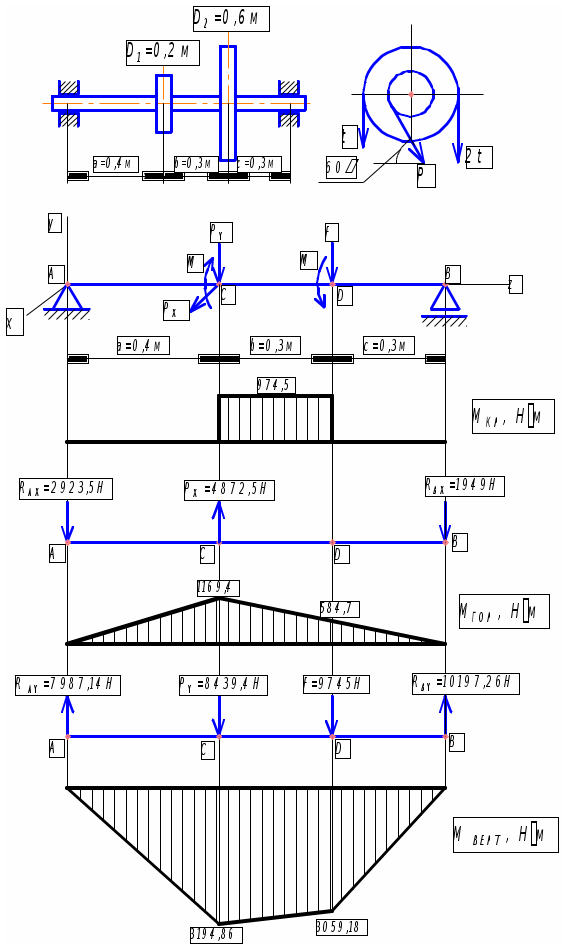 . Задача 3 Произвести проверку на усталостную прочность вала, рассчитанного в задаче 2. В расчетах принять, что нормальные напряжения изменяются по симметричному циклу, а касательные – по пульсационному. Обработка поверхности вала – тонкая обточка. Нормативный коэффициент запаса усталостной прочности равен 1,5. Дано: d= 80 мм;  ; ; ;тонкая обточка; σВ= 560 МПа; σТ= 280 МПа; σ-1= 250 МПа; τ-1= 150 МПа; [n]= 1,5 Решение: По результатам расчетов предыдущей задачи определили, что опасным является сечение С и вычислили требуемый диаметр вала. Определим характеристики циклов переменных напряжений от изгиба и кручения. Вычислим геометрические характеристики поперечного сечения вала. – осевой момент сопротивления  – полярный момент сопротивления  Наибольшие нормальные напряжения от изгиба в двух плоскостях 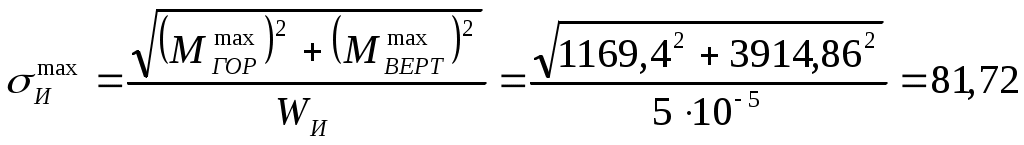 МПаНаименьшие нормальные напряжения от изгиб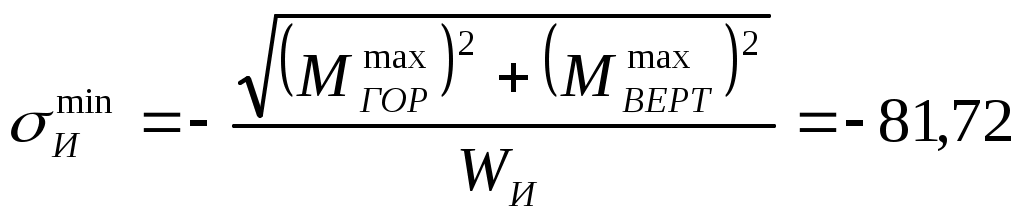а  МПа– среднее напряжение цикла  – амплитудное напряжение цикла  Коэффициент асимметрии равен: 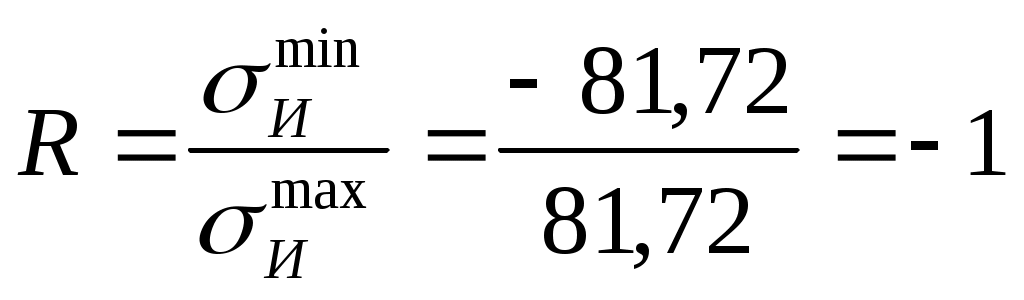 Наибольшие касательные напряжения  Наименьшие касательные напряжения  – среднее напряжение цикла  – амплитудное напряжение цикла  – коэффициент асимметрии цикла  Таким образом, нормальные напряжения от изгиба изменяются по симметричному циклу Rσ = –1, касательные напряжения от кручения – по отнулевому циклу Rτ = 0. Определим коэффициенты, учитывающие влияние конструктивно-технологических факторов и асимметрии циклов на предел выносливости по изгибу и кручению. Концентратором напряжений является шпоночный паз в месте посадки шкива. По таблицам для d = 80 мм и σВ = 560 МПа определяем коэффициенты предела выносливости вала при наличии шпоночного паза.  ,  Значение масштабного коэффициента при d = 80 мм  Коэффициент качества поверхности при тонкой обточке  .Примем коэффициенты чувствительности материала марки сталь 45 к асимметрии цикла по нормальным и касательным напряжениям ψσ = 0,1 ψτ = 0,05 Коэффициенты снижения предела выносливости с учетом всех факторов имеют следующие значения:   Определяем частные коэффициенты запаса прочности по выносливости   Общий коэффициент запаса прочности по выносливости равен:  Запас усталостной прочности вала не обеспечен, так как он меньше нормативного. Диаметр вала необходимо увеличить или ввести упрочняющую обработку. Задача 4 С заданной точкой М детали связана система декартовых координат x, y, z. Расчётом определены координатные напряжения в этой точке: σX,σY, σZ, τXY, τYZ, τXZ. Провести исследование напряжённо-деформированного состояния окрестности точки М. Материал детали считать упругим и изотропным, с модулем упругости E = 2·105 МПа и коэффициентом Пуассона = 0,3. Исследование напряжённо-деформированного состояния окрестности точки М детали выполнить в следующей последовательности. 1) Изобразить в аксонометрии единичный элемент, выделенный в окрестности точки М координатными сечениями, и показать напряжения, действующие на гранях этого элемента. 2) Записать тензор напряжений в этой точке в осях x, y, z. 3) Определить алгебраические инварианты тензора напряжений I1, I2, I3. 4) Записать алгебраические уравнения для определения главных напряжений и главных осей тензора напряжений. Вычислить главные напряжения σ1,σ2, σ3. 5) Вычислить направляющие косинусы главных осей напряжений I, II, III и изобразить в пространстве x, y, z оси главных напряжений I, II, III. 6) Записать тензор напряжений в точке М в главных осях I, II, III. Определить алгебраические инварианты этого тензора  . Проверить правильность вычисления главных напряжений, сравнив величины алгебраических инвариантов с величинами I1, I2, I3 соответственно.7) Определить нормальное σокти касательное τоктоктаэдрические напряжения. В пространстве главных осей I, II, III изобразить одну из октадрических площадок и показать нормальное и касательное напряжения, действующие на этой площадке. 8) Определить величину наибольшего касательного напряжения τmax . В пространстве главных осей I, II, III изобразить площадку, на которой действует наибольшее касательное напряжение и показать это напряжение. 9) Воспользовавшись соотношениями обобщённого закона Гука, определить величины главных деформаций ε1, ε2 , ε3. 10) Вычислить относительное изменение объема Δ. 11) Определить удельную потенциальную энергию упругой деформации окрестности точки М: - энергию изменения объёма WV, - энергию формоизменения WФ, - полную удельную энергию W . 12) Определить расчётное напряжение в точке М по гипотезе наибольших касательных напряжений  .13) Определить расчётное напряжение в точке М по гипотезе удельной потенциальной энергии формоизменения  .14) Определить расчётное напряжение в точке М по гипотезе прочности Мора  .Дано: σX = 60 МПа; σY = – 12 МПа; σZ = 19 МПа; τXY = 0; τYZ = 23 МПа; τXZ = 0; E = 2·105 МПа; = 0,3;  Решение: 1. Изображаем единичный элемент, выделенный в окрестности точки М координатными сечениями и показываем напряжения, действующие на гранях этого элемента. 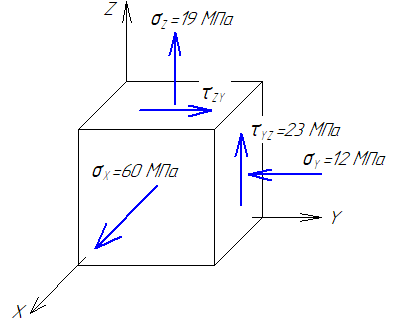 2. Записываем тензор напряжений. 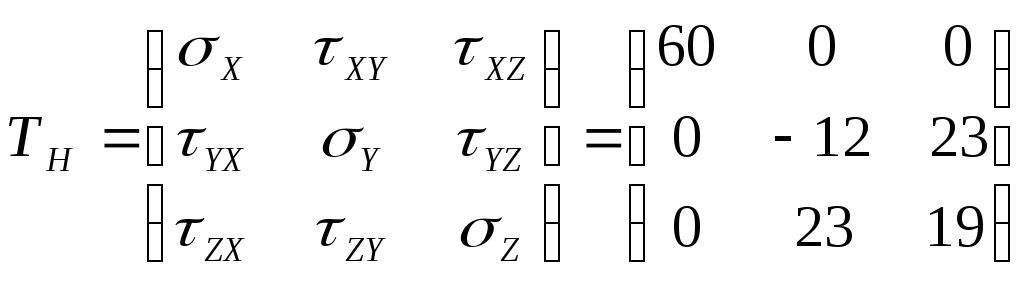 3. Определим алгебраические инварианты тензора напряжений    Так как второй и третий инварианты отличны от нуля, то рассматриваемое напряженное состояние является объемным. 4. Определяем главные напряжения и главные оси напряжений. Для этого записываем систему алгебраических уравнений относительно главных напряжений σ и направляющих косинусов l , m, n главных направлений. 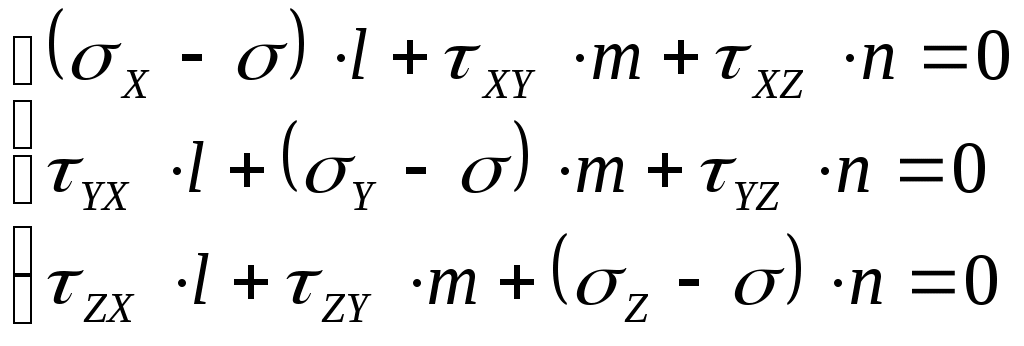 (1)которую дополняем условием:  (2)С учётом заданных величин компонентов тензора напряжений, отличных от нуля, приведём эту систему к виду 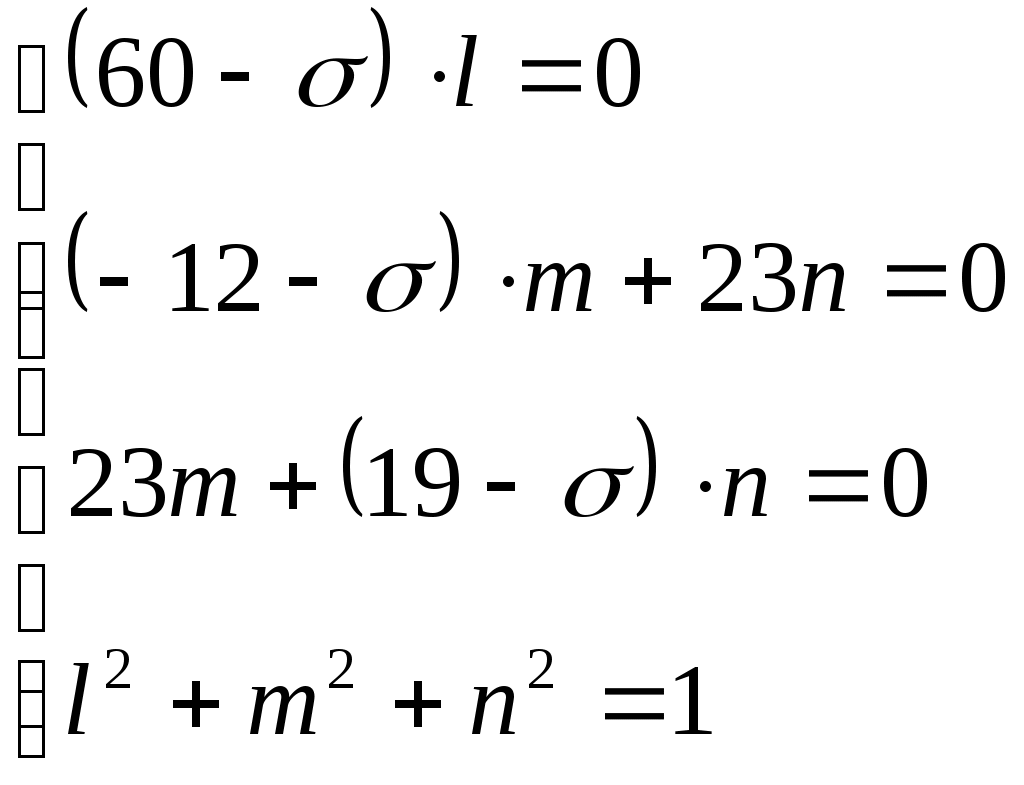 (3)Т.к. τXY = τXZ = 0, заключаем, что ось Xявляется одной из трёх главных осей напряжений, а напряжение σ = σX= 60 МПа– главным напряжением. Направляющие косинусы его направления, т.е. главной оси X l = 1; m = 0; n = 0. Главные оси напряжений взаимно перпендикулярны, поэтому следующие две главные оси напряжений располагаются в плоскости y, z. Для этих направлений n ≠ 0; l = 0; m ≠ 0. С учётом l= 0 систему разрешающих алгебраических уравнений (3) перепишем в виде 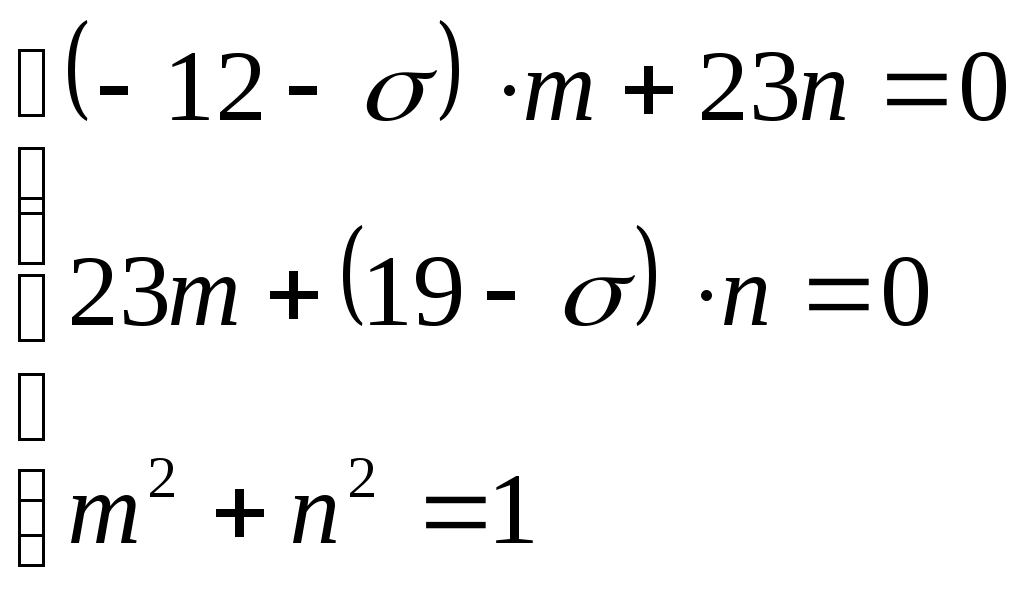 (4)Определим главные напряжения. Запишем определитель  Решим квадратное уравнение    5. Вычислим направляющие косинусы главных осей напряжений. Подставим в первое уравнение системы (4) 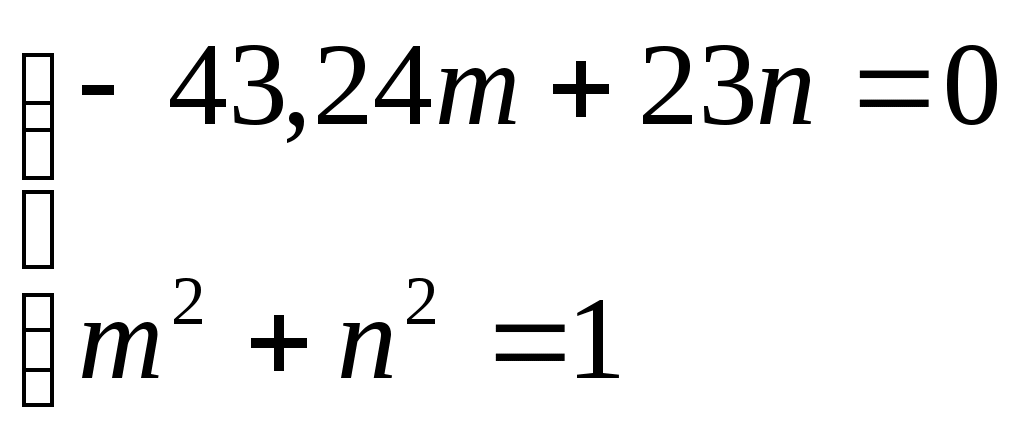, тогда уравнения примут вид: Получим    Подставим во второе уравнение системы (4) 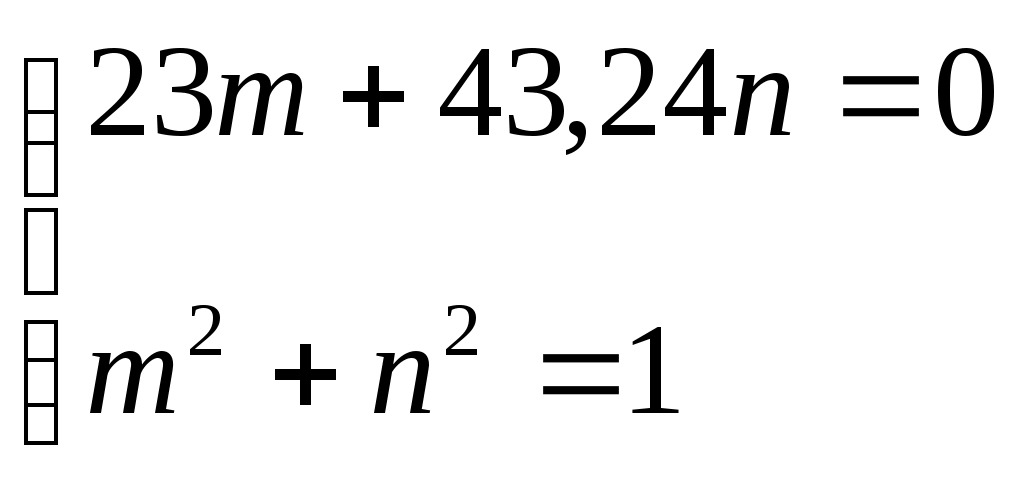, тогда уравнения примут вид: Получим    Выписываем найденные величины главных напряжений и соответствующие им направляюще косинусы главных напряжений. При этом для нумерации главных напряжений пользуемся принятым условием  .            В пространстве x, y, z по направляющим косинусам строим главные оси напряжений I, II, III. Изобразим элемент, выделенный главными площадками (главные оси повернуты). 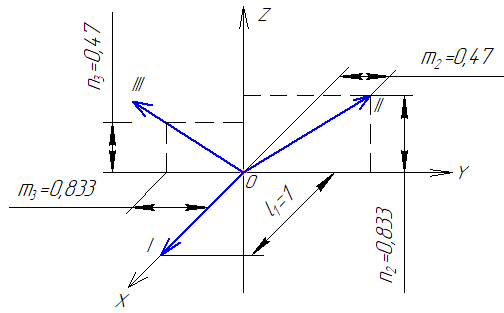 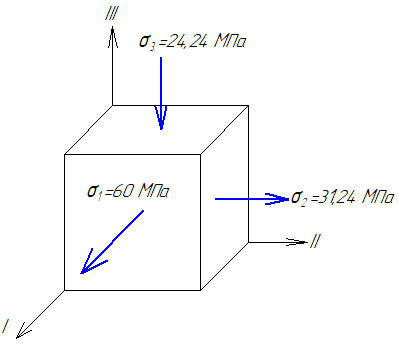 6. Записываем тензор напряжений в точке М в главных осях I, II, III и определяем алгебраические инварианты этого тензора 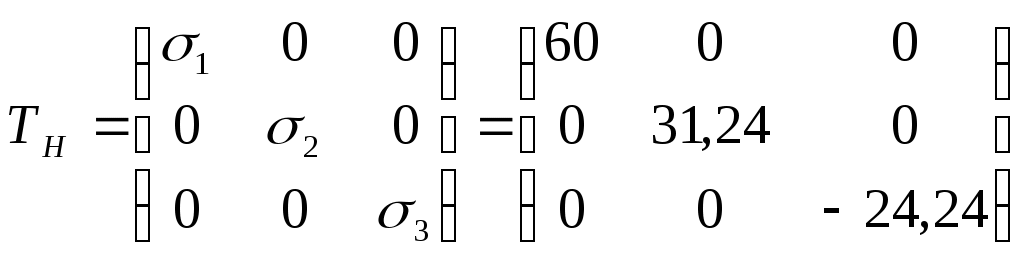    Сравнивая величины алгебраических инвариантов с инвариантами I1, I2, I3 соответственно, отмечаем их тождественность и, следовательно, достоверность величин главных напряжений. Незначительные расхождения вызваны результатом округления.7. Определяем величины нормального и касательного напряжений, действующих на октаэдрических площадках. 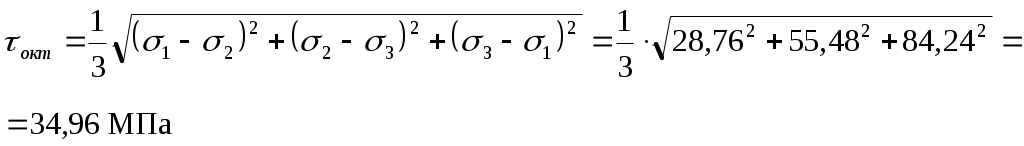  В пространстве главных направлений I, II, III изображаем одну из октаэдрических площадок и показываем напряжения, действующие на этой площадке (для октаэдрической площадки l = m = n = 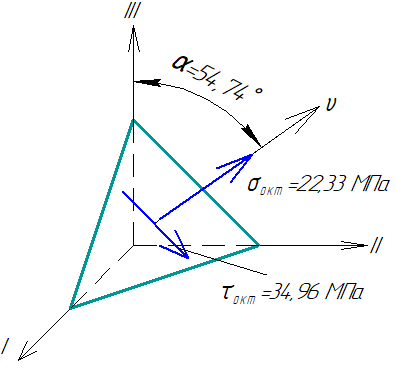 ). 8. Вычислим наибольшие касательные напряжения.  Напряжение τmax действует на площадке, параллельной главному направлению I и равнонаклонной к главным направлениям IIи III. Изображаем площадку, на которой действует напряжение τmax и показываем это напряжение. 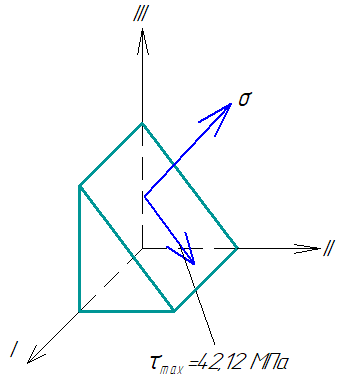 9. Определяем величины главных деформаций окрестности точки М. Считаем материал детали линейно-упругим и воспользуемся соотношениями обобщённого закона Гука.    10. Определяем относительное изменение объёма окрестности точки М.  11. Вычисляем удельную потенциальную энергию упругой деформации окрестности точки М. Удельная потенциальная энергия изменения объёма 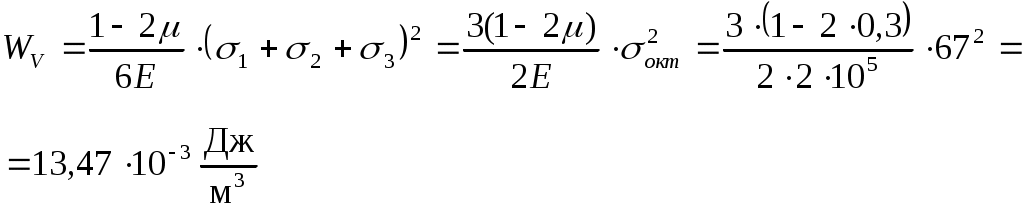 Удельная потенциальная энергия формоизменения 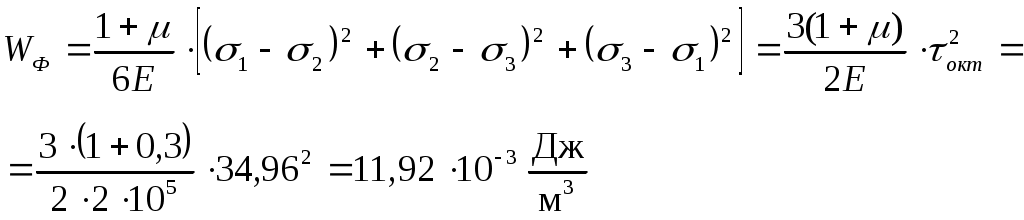 Полная удельная потенциальная энергия  12. Определяем расчётное напряжение в точке М по гипотезе наибольших касательных напряжений  13. Вычисляем расчётное напряжение в точке М по гипотезе удельной потенциальной энергии формоизменения 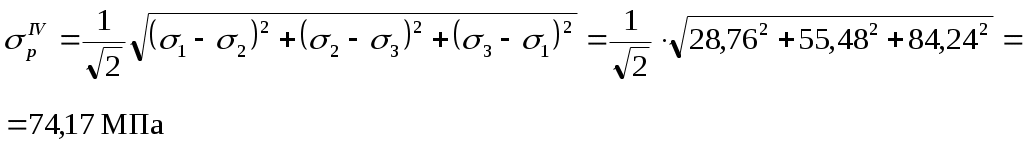 14. Вычисляем расчётное напряжение в точке М в соответствии с теорией прочности Мора  где  |