Домашнее задание СМ6-103 Зубарев Д.Б. Решение задач, определяющих надёжность изделий

• Название: Решение задач, определяющих надёжность изделий
• Дата: 11.05.2023
• Размер: 64.8 Kb.
• Имя файла: Домашнее задание СМ6-103 Зубарев Д.Б.docx
• Тип: Решение; #1121045

Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)» (МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ «СПЕЦИАЛЬНОЕ МАШИНОСТРОЕНИЕ»
КАФЕДРА «РАКЕТНЫЕ И ИМПУЛЬСНЫЕ СИСТЕМЫ» (СМ-6)


ДОМАШНЕЕ ЗАДАНИЕ

ПО ДИСЦИПЛИНЕ:

Надёжность ракетного оружия

НА ТЕМУ:

Решение задач, определяющих надёжность изделий

ВАРИАНТ №

25

Выполнил: студент группы	СМ6-103				Зубарев Д. Б.
			(подпись, дата)		(И.О. Фамилия)

Проверил					Кондратьев И. М.
			(подпись, дата)		(И.О. Фамилия)

Москва, 2023 г.

ЗАДАЧА 1

Частота отказов изделий при испытании их в течение 1000 ч составила 5 ·10^-5 1/ч, а наблюдаемое число отказов – 50. Найти число изделий, поставленных на испытания.

Решение:

Частота отказов изделий при испытании вычисляется по формуле:



где – число отказавших изделий в интервале наработки ; – длительность интервала наработки; общее число изделий, поставленных на испытания.

Отсюда число изделий , поставленных на испытания, находится по формуле:



ЗАДАЧА 2

Схема расчета надежности системы приведена на рис. 1 (А, Б, В, Г − блоки системы). Определить вероятность безотказной работы P_c(t) системы.



Рис. 1. Схема расчета надежности системы

Решение:

Вероятность безотказной работы системы равна:



где вероятность безотказной работы блока А; вероятность безотказной работы блока Б; вероятность безотказной работы блока В; вероятность безотказной работы блока Г.

Блок А – без резервирования ( );

Блок Б – резервирование замещением в режиме ненагруженного резерва;

Блок В – без резервирования ( );

Блок Г – режим постоянного резервирования ( ).

Для блока А вероятность безотказной работы равна:



где вероятность безотказной работы -го элемента блока А, .



Тогда .

Для блока Б вероятность безотказной работы равна:



где по условию и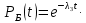

Тогда (1+ .

Для блока В вероятность безотказной работы равна:



где вероятность безотказной работы -го элемента блока В.

Так как то

Для блока Г вероятность безотказной работы равна:



где вероятность безотказной работы -го элемента блока Г, .



Тогда .

Найдем вероятность безотказной работы системы:



ЗАДАЧА 3

Вероятность отказов стартерного механизма двигателя должна быть менее 0,08. Найти браковочное число A₁ с риском заказчика β≈ 0,10 при 1000 запусков двигателя.

Решение:

При контроле больших партий со сравнительно невысокой надежностью риск заказчика определяется по приближенной формуле:



где – верхняя граница вероятности отказа; браковочное число; число выбранных экземпляров для контроля надежности из партии объемом , в данном случае, это число запусков двигателя; функция Лапласа.

Найдем браковочное число , соответствующее верхней границе вероятности отказа :





При значении функции Лапласа 0,4 значение аргумента 1,28. Тогда имеем:





9

Так как вероятность отказов должна быть менее 0,08, то браковочное число берём .