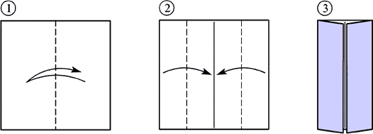
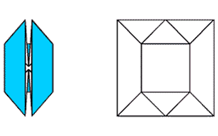
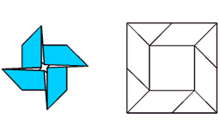
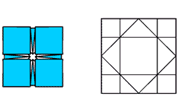
Оригами в математике. Решение задач
 Скачать 0.69 Mb.
|
|
Оглавление
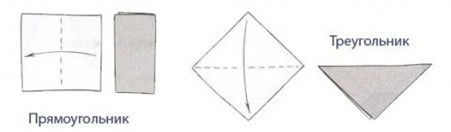
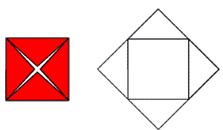
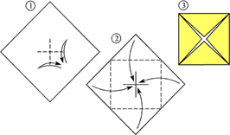
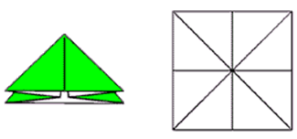
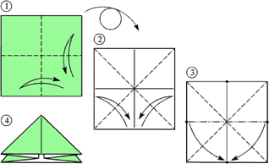
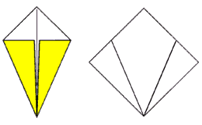
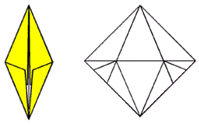
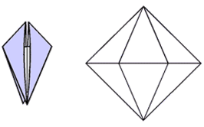
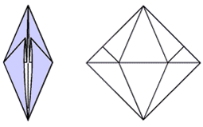
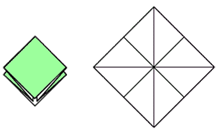
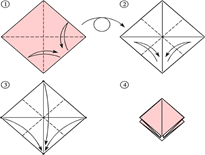
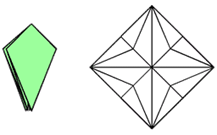
Введение. Оригами - удивительное искусство бумажной пластики. Оригами — это японское искусство складывания бумаги, образовано от японского («oru» - (складывать) и «kami» - (бумага)). Сегодня множество людей во всем мире увлекаются искусством «оригами».Складывая фигурки оригами, сталкиваешься с математическими понятиями. Мне стало интересно, как связаны искусство складывания фигурок из бумаги оригами и математика. Актуальность исследования состоит в том, что в последнее время учащиеся всё с большей неохотой относятся к учёбе, и, в частности, к математике. Своей работой я хотел показать, что математика интересная, творческая наука и при помощи оригами из листа обычной бумаги можно не только творить самые невероятные вещи, но и делать различные геометрические построения без циркуля и линейки. Во время создания нужной фигурки – работает моторика рук, развивается мышление. Новизна моей работы применение оригинальных идей решения задач с помощью листа бумаги. Цель: изучить происхождение оригами и связь искусства оригами с математикой, определить область применения техники оригами для развития пространственного мышления Задачи: 1. Определить, что называют оригами 2. Рассмотреть базовые формы и приемы оригами 3. Изучить понятие, виды, историю происхождения оригами. 4. Проанализировать связь оригами и математики. Проблема: может ли оригами помочь в решении некоторых геометрических задач? Объект исследования: оригами. Предмет исследования: свойства геометрических фигур. Методы исследования: - поиск информации из разных источников (специальная литература, интернет-ресурсы); - обработка информации; - анализ и обобщение информации по теме. Продукт: Создать «Памятку» для учителей и обучающихся по применению основ оригамидля изучения геометрии. Практическая значимость:эту работу можно использовать на уроках математики, во внеурочной деятельности. Гипотеза: Искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения. Данная работа знакомит с математическими основами оригами. Оригами развивает не только пространственное воображение, память, творчески-исследовательские способности, но и развивает любознательный интерес к предмету. Глава 1. Искусство оригами Каждый человек наверняка хоть раз в жизни создавал самое простенькое изделие из квадратного листа бумаги – кораблик или тюльпанчик. А в те времена, когда в магазинах не было соломенных шляп и панам, люди летом нередко сооружали себе «пилотку» из газеты. И бумажные кораблики, и пилотка сделаны по принципу «оригами». В наше время оригами перестало быть только игрушкой. Этим искусством заинтересовались ученые и конструкторы. Проходят научные симпозиумы по оригами. Но детей, конечно, больше всего интересует оригами как возможность создать новую игрушку. А можно создать новые, свои собственные объемные фигурки из бумаги. Итак, оригами – это искусство складывания из бумаги. 1.1. История оригами В переводе с японского «оригами» означает «сложенная бумага», в стране восходящего солнца искусство оригами называют искусством целого листа. Это одно из самых главных правил оригами — не прибавлять и не вычитать ничего лишнего. Первые очерки о фигурках из бумаги появились в еще в эпохе Хэйан. Самураи, которые жили в то время, делая подарки крепили к ним отделку из бумажных ленточек - носи.Хотя, в противовес этим фактам, многие ученые считают, что искусство оригами появилось задолго до появления бумаги. Есть предположения, что сперва техника оригами использовалась для украшения национальных японских костюмов разнообразными драпировками из тканей. И до нас дошли только самые изысканные фигурки, истории о которых передавались из уст в уста. Так как японцы считают оригами одним из видов искусства, они создали для него специальные каноны: оригами может рождаться только при помощи сгибания листа. Если бумага подвергается нарезанию или склеиванию, то это не оригами. Автором этих канонов является Акира Йошизава. 1.2. Виды и техники оригами Простое оригами — стиль оригами, придуманный британским оригамистом Джоном Смитом. Целью оригами является облегчение занятий неопытным оригамистам, а также людям с ограниченными двигательными навыками. Модульное оригами- оригами, в котором целая фигура собирается из многих одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга, появляющаяся при этом сила трения не даёт конструкции распасться. Одним из наиболее часто встречающихся объектов модульного оригами является кусудама, объёмное тело шарообразной формы. Складывание по развёртке. Развёртка— один из видов диаграмм оригами, представляющий собой чертёж, на котором изображены все складки готовой модели. Мокрое оригами. Бумага смачивается водой, от этого она становится более пластичной. В результате работы со смоченной бумагой получаются плавные формы. Изделия похожи на папье-маше. Киригами. Вид работы с бумагой при помощи ножниц. Ножницы дают большую свободу действий и более чёткие формы. Наноригами. Сложная разновидность оригами. Это трёхмерный конструктор с малюсенькими элементами. Фигуры в оригами выполняются из геометрических фигур: квадрата, треугольника, прямоугольника, пяти-, шести-, восьмиугольников, и даже круга. То есть все фигуры в оригами выполняются из геометрических фигур, значит это одна из точек прикосновения оригами с математикой. 1.3. Базовые формы оригами. С древних времён в японском оригами существуют некоторые формы, которые принято считать базовыми. Это стандартные, легко распознаваемые заготовки, из которых впоследствии можно получить сотни вариаций. На самых первых этапах работы квадратный лист можно сложить несколькими способами. Их немного — одиннадцать, и у каждой своё имя. (Приложение № 1) Глава 2. Оригами – это математика! Как связано искусство оригами и точная наука математика. Этот вопрос я решил изучить. Я проанализировал базовые формы оригами и заметил, что уже при первом знакомстве с этим искусством мы узнаем о таких простых формах, как прямоугольник и треугольник. Когда складываем простую форму, то знакомимся с квадратом, согнув углы которого к центру можно увидеть, что квадрат может состоять из четырёх одинаковых треугольников. Складывая форму «Воздушный змей», знакомимся с ромбом. Азбука оригами включает в себя такие геометрические понятия, как точка и линия.(Приложение №2) Таким образом, оригами и математика, а именно геометрия, неразрывно связаны. Множество понятий из математики, такие как точка, линия, квадрат, прямоугольник, треугольник используем мы при изготовлении оригами. 2.1. Некоторые примеры связи математики и оригами. Согласно классическому оригами, объектом складывания являетсянеразмеченный квадратный лист бумаги, без разрезов. С точки зрения математики, целью оригамиста является точное определение местоположения одной или более точек листа, задающих складки, необходимые для формирования окончательного объекта. Процесс складывания подразумевает выполнение последовательности точно определенных действий по следующим правилам: - линия определяется либо краем листа, либо линией сгиба бумаги. - точки определяются пересечениями линий. - все складки определяются единственным образом путем совмещения различных элементов листа - линий или точек. - сгиб формируется единственной складкой, причем в результатескладывания фигура остается плоской. В процессе складывания фигур оригами мы знакомимся с различными геометрическими фигурами: треугольником, квадратом, трапецией и т.д., учимся легко ориентироваться в пространстве и на листе бумаги, делить целое на части, находить вертикаль, горизонталь, диагональ, узнаём многое другое, что относится к геометрии и математике. 2.2. Оригаметрия в математике Оригаметрия — это новая наука на стыке двух: оригами и геометрии. Это оригинальный подход к решению геометрических задач. Основные понятия оригаметрии: точка; линия сгиба; квадратный лист бумаги. Основные отношения: линия сгиба проходит через точку; точка принадлежит линии сгиба. Возможности построения при помощи перегибания квадратного листа бумаги намного больше, чем при использовании классических чертёжных инструментов. В оригаметрии роль прямых будут играть края листа и линии сгибов, образующиеся при его перегибании.Роль точек - вершины углов листа и точки пересечения линий сгибов друг с другом или с краями листов Любая оригамская задачасостоит из:постановки задачи, оригамского решения, проверки или способа построения, математического обоснования, то есть доказательства того, что в результате действительно получается фигура с требуемыми свойствами. Математика — это одна из сторон оригами и наоборот оригами является одной из направляющих математики. Большинство классических моделей в оригами выполняются из квадрата. В процессе изготовления простых моделей мы знакомимся с очень нужными понятиями. 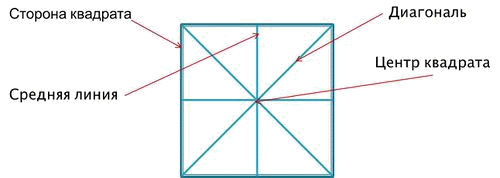 Деление на части является основами раздела математики - геометрии!!! П  осмотрим на обычный лист бумаги, как на средство обучения одному из сложных предметов - геометрии. Проведем исследование листа бумаги. - Какую он имеет форму- прямоугольник, квадрат - Каждая вершина угла этого листа -вершина прямоугольника - Край листа -сторона, отрезок. 2.3. Доказательство некоторых теорем с помощью оригами. Теорема 1. В прямоугольном треугольнике катет, лежащий напротив угла в 30 градусов равен половине гипотенузы (свойство прямоугольного треугольника)  Доказательство: 1) Можно найти середину гипотенузы, простым сгибом пополам. 2) Сравним длину катета, лежащего напротив угла в 30 градусов с длиной гипотенузы, простым наложением. И у нас получится, что мы попали в середину.  Теорема 2. Сумма острых углов прямоугольного треугольника равна 900 Доказательство: 1) Согните треугольник.   Острые углы при наложении составляют прямой угол, который равен 900. 2.4. Решение задач Существует много типов задач, к которым можно применить метод сгибов. Среди них задачи на построение, на доказательство, на нахождение линейных размеров искомых фигур, их площадей, периметров и т. д. Чтобы проиллюстрировать красоту и возможности указанного метода, рассмотрим несколько задач. З 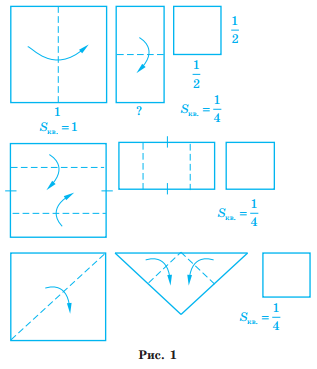 адача 1. Из данного квадрата получите квадрат, площадь которого в 4 раза меньше площади данного. Решение. Из одного квадрата получили четыре равных квадрата (они совпадают при наложении), а значит, и площадь каждого равна четвертой части исходного квадрата. З 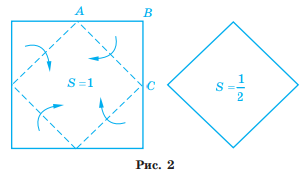 адача 2. Из данного квадрата получите квадрат, площадь которого в 2 раза меньше площади данного. Решение. Оригами-решение можно предложить следующее (рис. 2): Это решение также очевидно С помощью сгибов из квадрата можно получить другие правильныемногоугольники. С помощью оригами решаются геометрические задачи на плоскости. Складывание многоугольников – увлекательнейшее занятие, но вместе с тем и не простое. Оно требует аккуратности, точности и высокого сосредоточения внимания. Существует пять правильных многогранников, которые называют Платоновыми телами.(Приложение №2).Они составлены из правильных многоугольников (тетраэдр – 4 треугольника, октаэдр – 8 треугольников, икосаэдр – 20 треугольников, куб – 6 квадратов, додекаэдр – 12 пятиугольников). Неоценимую помощь в изготовлении многогранников может принести оригами. Вы можете изготовить многогранник любого размера без всякой выкройки. Нужно только выбрать размер листа бумаги. Кроме того,оригамный многогранник всегда можно разобрать, а его модули при этом не займут много места. Оригами можно использовать на занятиях по математике в таких заданиях, как: а) найти горизонтальные, вертикальные, наклонные линии; б) найти все квадраты; в) найти все треугольники; г) дать название изображениям; д) складывание квадрата, смежные стороны, диагональ. Заключение. Таинственный мир превращенья бумаги… Здесь все чародеи, волшебники, маги. Творят они сказки своими руками. И мир тот чудесный зовут ОРИГАМИ Марданова Е.У. Так для чего же нужно оригами? Оригами, прежде всего, – искусство, призванное дарить людям радость. Все фигуры в оригами выполняются из геометрических фигур, значит это одна из точек прикосновения оригами с математикой. Но в оригами фигуры можно построить без чертежных инструментов, используя несколько сгибов. При работе с квадратом знакомимся с понятиями: угол, сторона, диагональ, центр, средняя линия, вершина, деление отрезка на части, угла на части, со способами складывания квадрата и складывания из квадрата других геометрических фигур. Таким образом, с помощью оригами решаются геометрические задачи на плоскости. По результатам моего исследования можно сделать вывод, что гипотеза подтвердилась. В заключение выделим наиболее существенные моменты. Оригами как основа различных направлений искусства является наиболее логичной и гармоничной формой изучения геометрии. Логика здесь выступает как средство подтверждения наглядности и практической значимости. Выполняя геометрические фигуры в технике оригами, обучающиеся знакомятся с новыми геометрическими понятиями, основными определениями и наглядно изучают закономерности поведения двухмерной плоскости в трехмерном пространстве. Правильно гласит великая китайская мудрость: я слышу и забываю, я вижу и запоминаю, я делаю и понимаю. В голове удерживаются только те знания, которые применяются на практике. Список используемых источников и литературы Афонькин, С. Ю., Капитонова, И. В. Оригами и геометрия – Чебоксары: ЧГУ, 1993. Белим, С. Н. Задачи по геометрии, решаемые методами складывания (оригами). – М.: Аким, 1997. Ильин И.С., Ильин С.Д. «Оригами. Лучшие модели.- М. ООО ТД «Издательство . Мир книги», 2010г. С. Н. Белим Задачи по геометрии, решаемые методами оригами. – М.: изд. «Аким», 1998г., Ткачева М.В. Домашняя математика. М.: Просвещение, 1994. Уроки оригами в школе и дома: учебное пособие. Шеремет Г. Оригами помогает изучать математику. / Математика. – 2007. № 19. Ресурсы интернета http://origamis.ru http://www.vlasta-idea.ru http://bebi.lv http://www.origami.kulichki.ru/modules.php?name=Pages&go=page&pid=2 http://www.origami.ru Приложение № 1 Базовые формы
Приложение № 2 Правильные многоугольники и способы их изготовления из квадрата с помощью оригаметрии Треугольник Пятиугольник 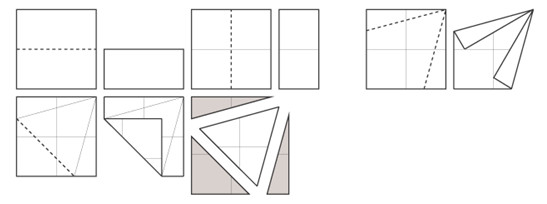 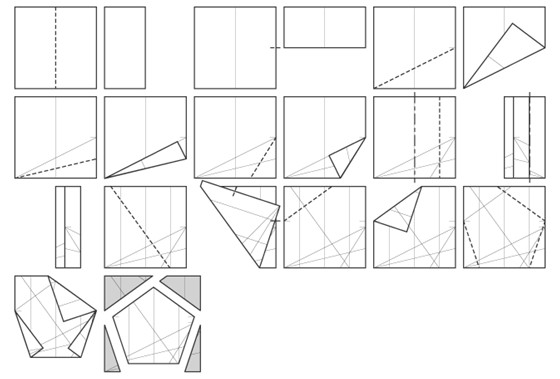 Шестиугольник Восьмиугольник     |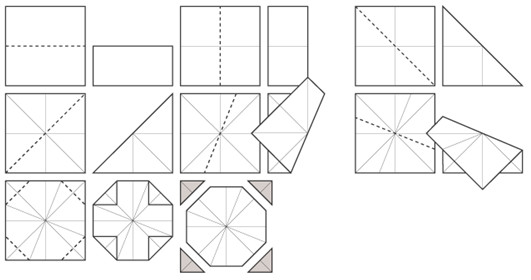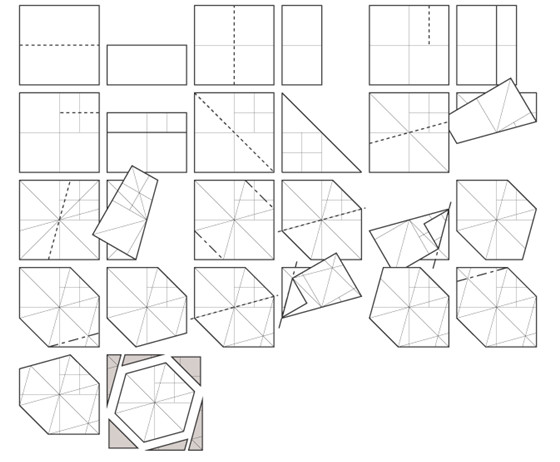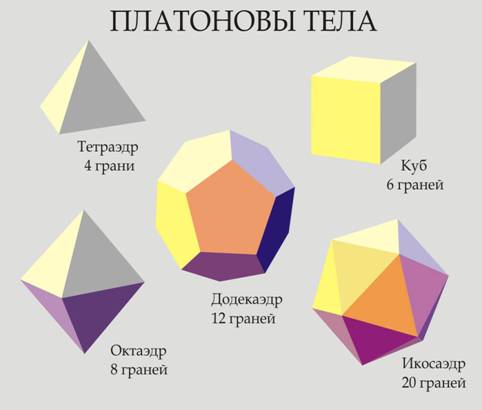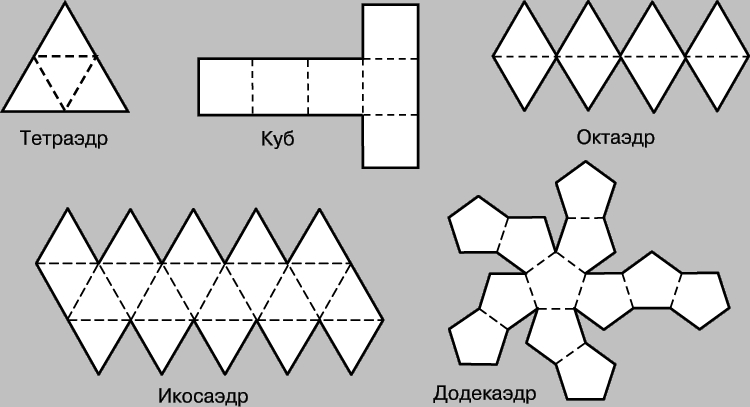
