Задачи статистика. Решение. Значит, 75% из всего количества старых вагонов на ремонте
 Скачать 32.18 Kb. Скачать 32.18 Kb.
|
Вариант 1В двух пеналах находятся ручки двух цветов. В первом пенале – 6 красных и 4 черных ручки, во втором – 7 красных и 3 черных ручки. Из каждого пенала взяли по одной ручке, а потом из этих двух ручек наудачу взяли одну. Какова вероятность того, что выбрана красная ручка? Ответ: Вероятность,что обе красные Р1=6/10 * 7/10= 42/100 Вероятность,что обе черные Р2=4/10 * 3/10= 12//100 Вероятность, что одна-красная Р3= 1 - 42/100 - 12/100=46/100 Вероятность того, что в случае Р3 вытащат красную Р4=1/2 * 46/100=23/100 Искомая вероятность Р= Р1+Р4= 42/100 + 23/100 = 65/100 Вероятность попадания в цель стрелком при одном выстреле равна 0,7. Сделано 10 выстрелов. Какова вероятность того, что стрелок промахнулся не более двух раз? Ответ: P(В) = 0,3 * 0,7 = 0,21.Осталось найти сумму вероятностей:P(А) + P(В) =0,7 + 0,21 = 0,91. На линиях метро курсируют 25% вагонов старого образца. Найти вероятность того, что среди тысячи вагонов, находящихся в ремонте, больше 130 старого образца? Решение. Значит, 75% из всего количества старых вагонов на ремонте. Всего на ремонте 1000 вагонов. Среди них, 130 старого образца. 1000-130=870 (вагонов нового образца на ремонте) n=1000 p=0,75 q=0,25 k= 870 Справедлива формула,   P(870,1000)=1/13,69•ϕ(870-750/13,69)=1/13,69•8,77=0,64 1-0,64=0,36 Дискретная случайная величина 𝜉 задана рядом распределения:
Найти: а) неизвестную вероятность 𝑝; б) функцию распределения𝐹(𝑥) и построить её график; в) математическое ожидание𝑀[𝜉]; г) дисперсию𝐷[𝜉]; д) 𝑃 (0 <𝜉≤ 5). P=1-0.7=0.3
Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. M[x] = (-3)*0.1 + (-1)*0.2 + 2*0.3 + 5*0.3 + 8*0.1 = 2.4 Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]. D[X] = 32*0.1 + 12*0.2 + 22*0.3 + 52*0.3 + 82*0.1 - 2.42 = 10.44 Среднее квадратическое отклонение σ(x). Функция распределения F(X). F(x≤-3) = 0 F(-3< x ≤-1) = 0.1 F(-1< x ≤2) = 0.2 + 0.1 = 0.3 F(2< x ≤5) = 0.3 + 0.3 = 0.6 F(5< x ≤8) = 0.3 + 0.6 = 0.9 F(x>8) = 1  Вероятность. Вероятность попадания СВ в тот ли иной интервал находится по формуле: P(a ≤ X < b) = F(b) - F(a) Найдем вероятность того, что СВ будет находиться в интервале X < 0 P(X < 0) = F(0) = 0.3 В коробке 10 маркеров, из которых два маркера уже не пишут. Наудачу берут три маркера. Случайная величина 𝜉 – число пишущих маркеров среди взятых. Построить вероятностный ряд для 𝜉. Найти ее 𝑀[𝜉] и 𝐷[𝜉]. С103 = 10!/(3!*7!)= 10*9*8/6=120 - количество способов выбрать 3 карандаша из 10 p(x0) - вер., что извлекли 3 карандаша, среди них нет красного. С83 - кол-во способов выбрать 3 не красных карандаша. С83 = 8!/(3!*5!) = 8*7*6/6=56 р(х0)= С83 /С103 = 56/120 = 7/15 р(х1) = 2*С82 / С103 = 2*8*7/2 /120 = 14/30 - вер, что 1 красный 2 - нет Р(х2) = С22*С81/120 = 1*8/120 = 1/15 - вер, что 2 красных, 1 - нет Математическое ожидание 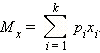 Мх= 0*7/15 + 1*21/30 + 2*1/15 = 25/30 = 5/6 Дисперсия случайной величины  Dx= p0(x0-Mx)2+ p1(x1-Mx)2+ p2(x2-Mx)2 Dx = 7/15*(0 - 5/6)2 + 21/30*(1-5/6)2 + 1/15*(2- 5/6)2 =0,324+0,01944+0,091=0,4344 Непрерывная случайная величина 𝜉 задана с помощью функции плотности распределения вероятностей𝑓(𝑥):  Найти: а) параметр 𝐶; б) функцию распределения 𝐹(𝑥) и построить ее график. в) математическое ожидание𝑀[𝜉]и дисперсию 𝐷[𝜉]. г) 𝑃 (0 <𝜉≤ 5). Случайная величина 𝜉 распределена равномерно на [2; 7]. Написать𝑓(𝑥) и 𝐹(𝑥). Найти 𝑀[𝜉] и 𝐷[𝜉]. Вычислить 𝑃 (−4 ≤ 𝜉 ≤ 5). Случайная величина 𝜉 распределена нормально с математическим ожиданием 𝑀[𝜉] = 2 и дисперсией 𝐷 𝜉 = 100. Написать ее функцию плотности распределения вероятностей 𝑓(𝑥)и вычислить 𝑃 (−5 ≤ 𝜉 ≤ 16). |
