Контрольная Работа ЭЛЕКТРОТЕХ. Решение Зная напряжение и мощность, найдем общую силу тока. PUi iPU2001002A
 Скачать 285.38 Kb. Скачать 285.38 Kb.
|
|
1. Линейные цепи постоянного тока Задание 1.1. В цепи, показанной на схеме, известны сопротивления R1 и R1. Напряжение на зажимах цепи равно U. Мощность, измеряемая ваттметром, равна P. Определить сопротивление R3 и токи во всех ветвях цепи. Составить баланс мощностей. 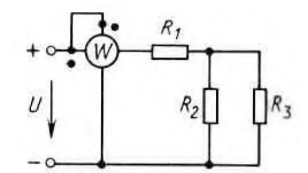 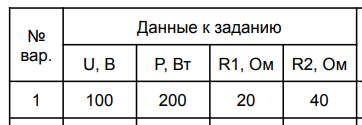 Решение Зная напряжение и мощность, найдем общую силу тока. P=U*I I=P/U=200/100=2A Сила тока на первом сопротивление равна общему току. Найдем напряжение на первом сопротивлении с помощью Закона Ома. I=U/R U1=I*R1=2*20=40В Найдем напряжение на втором и третьем сопротивлении. U=U1+U2 U2=U-U1=100-40=60В Найдем силу тока на втором сопротивлении I2=U2/R2=60/40=1.25A I3=I-I2=2-1.25=0.75A Найдем сопротивление R3 R3=U2/I3=60/0.75=80 Ом Проверим баланс мощностей: Мощность на входе равна сумме мощностей на каждом потребителе: P=P1+P2+P3=40*2+1.25*60+0.75*60=200 Вт Баланс мощностей совпадает. Задание 1.2. В цепи, показанной на схеме, э.д.с. источников питания равны E1, Е2, Е3, а сопротивления ветвей соответственно R1, R2, R3, R4 (включая внутренние сопротивления источников питания). Используя метод узловых потенциалов, определить токи в ветвях цепи и режим работы каждого из источников. Составить баланс мощностей. 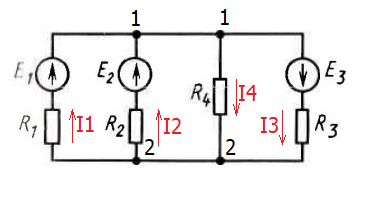  Решение 1. Находим напряжение между двумя узлами по методу двух узлов.  При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус — если направлена от узла a к узлу b. 2. Находим токи по закону Ома (по закону Ома для ветви с ЭДС) 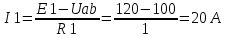   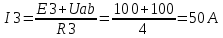 Правильность решения проверим по первому закону Кирхгофа I1+I2-I3-I4=0 20+50−20-50=0. Проверим баланс мощностей. E1*R1+E2*R2+E3*R3=I12R1+ I22R2+ I32R3+ I42R4 120*20+200*50+100*50=202*1+502*2+502*4+202*5 17400Вт=17400Вт Баланс совпадает. 2. Линейные цепи гармонического тока Задание 2.1. В цепи, показанной на схеме, активные и реактивные сопротивления ветвей соответственно равны R1, X1, R2, X2. Ток, измеренный амперметром А, равен I1. Используя метод комплексных амплитуд, определить: а) показания вольтметра и ваттметра; б) коэффициент мощности на зажимах цепи. Построить топологическую диаграмму векторов токов и напряжения цепи. 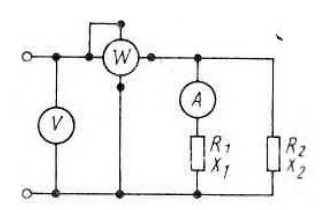  Согласно исходных данных: 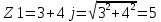 Ом Ом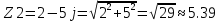 Ом ОмНайдем напряжение в параллельных ветвях: I1=U/Z1; U=Z1*I1=3*5=15 В Найдем ток в параллельной ветви: I2=U/Z2=15/5.39=2.78A Найдём углы сдвига фаз между токами I1 и I2 и напряжением U. φ1=arctg[XL/R1]=arctg[4/3]=53° φ2=arctg[-XC/R2]=arctg[-5/2]=-68° Находим активные составляющие токов I1, I2 и I. Ia1=I1cosφ1=3×cos(53°)=1,81 A ; Ia2=I2cosφ2=2.78×cos(-68°)=1.04 A ; Ia=Ia1+Ia2=1.81+1.04=2.85 A Находим реактивные составляющие токов I1 , I2 и I. Ip1=I1sinφ1=3×sin(53°)=2.4 A ; Ip2=I2sinφ2=2.78×sin(-68°)=-2.58 A Ip=Ip1+Ip2=2.4-2.58=-0,18 А Полный ток в неразветвленной части цепи : 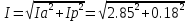 =2.86 A. =2.86 A.Найдём коэффициент мощности цепи : cosφ=Ia/I=2.85/2.86=1 В цепи имеет место резонанс токов. Найдём активную P, реактивную Q и полную S мощности цепи. P=I12R1+I22R2=1.812×3+1.042×2=11.99 Вт Q=I12XL-I22XC=1.812×4-1.042×5=7.69 вар 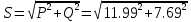 =4045 В∙А. =4045 В∙А.Для построения векторной диаграммы найдём длины векторов : Для удобства берем за 1 см отрезка 1А. Построение векторной диаграммы начинаем с построения вектора напряжения U , который откладываем горизонтально. Вектор тока Ia1 откладываем параллельно вектору напряжения U. От конца вектора Ia1 откладываем вектор тока Ip1 перпендикулярно вектору U в сторону отставания от него. Геометрическая сумма векторов Ia1 и Ip1 дают вектор I1. Вектор тока Ia2 откладываем параллельно вектору напряжения U. От конца вектора Ia2 откладываем вектор тока Ip2 перпендикулярно вектору напряжения U в сторону его опережения. Геометрическая сумма векторов Ia2 и Ip2 дают вектор I2. Вектор I строим как геометрическая сумма векторов I1 и I2 , или как геометрическую сумму векторов Ia и Ip. 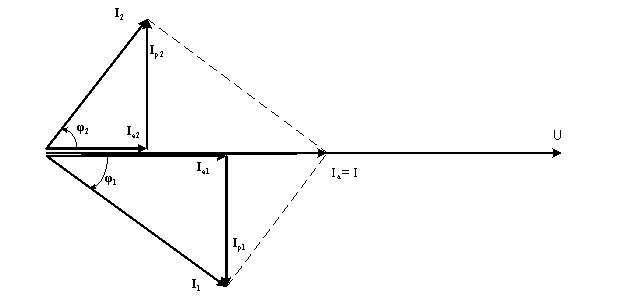 Задание 2.2. В цепи, показанной на схеме, напряжения на зажимах цепи и конденсатора соответственно равны I, U, UC. В цепи имеет место режим резонанса напряжений. Частота f = 50 Гц. Определить: а) напряжение на зажимах катушки UК; б) емкость C конденсатора, активное сопротивление RК и индуктивность LК катушки. Построить топологическую диаграмму векторов тока и напряжений цепи. 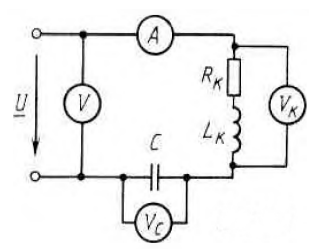 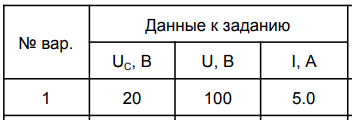 Полное сопротивление цепи: I=U/Z, откуда Z=U/I=100/5=20 Ом Напряжение на катушке Uk=U-Uc=100-20=80 В Найдём индуктивность катушки, которую нужно включить в сеть с конденсатором, чтобы в цепи возник резонанс напряжений. Условие резонанса: XL0=XC=Uc/I=20/5=4 Ом Индуктивность катушки: L0=XL0/(2πf)=4/(2×3.14×50)=0.013 Гн=13 мГн. Находим ёмкость конденсатора : C=1/(2πfXC)=1/(2×50×3.14×4)=796×10-6 Ф=796 мкФ. Полное сопротивление цепи в режиме резонанса напряжений равно активному сопротивлению: z0=R=20 Ом. Для построения векторной диаграммы найдём длины векторов : ℓUa=100/5=20 см ; ℓUc0=20/5=4 см. Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua0 откладываем параллельно вектору тока I. От конца вектора Ua0 откладываем вектор напряжение UC0 перпендикулярно вектору тока I в сторону отставания от него. От конца вектора UC0 откладываем вектор напряжения UL0 перпендикулярно вектору тока I в сторону его опережения (по модулю вектора UC0 и UL0 равны). Геометрическая сумма векторов Ua0 , UC0 и UL0 даёт вектор напряжения U, приложенного к цепи (U=Ua0).  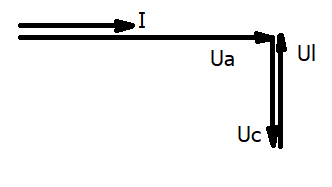 3. Трёхфазные цепи Задание 3.1. К трехфазной линии с линейным напряжением UЛ подключены три одинаковых приёмника, соединённых звездой. Активное и реактивное сопротивления каждого приемника равны R и X. Определить токи в фазах нагрузки и линейных проводах, а также потребляемую нагрузкой активную мощность в режимах: а) симметричном трехфазном; б) при обрыве одной фазы нагрузки; в) при коротком замыкании той же фазы нагрузки. Построить для всех трёх режимов топографические диаграммы напряжений и показать на них векторы токов. 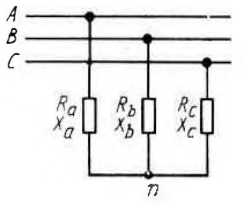 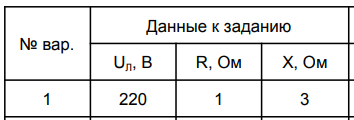 Так как приёмник симметричный, то полное сопротивление фаз : Z=ZA=ZB=ZC= 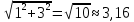 Ом ОмФазное напряжение : Uф= 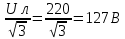 Так как приёмник соединён звездой, то фазные и линейные токи равны : Так как приёмник соединён звездой, то фазные и линейные токи равны :Iф=Iл=Uф/Z=127/3,16=40,19 А. Коэффициент мощности цепи : cosφ=R/Z=1/3,16=0.3 ; угол сдвига фаз между током Iф и напряжением Uф : φ=arccos(0.3)=72° Активная мощность цепи : P=3Iф2R=3×40,192×1=4846 Вт. Реактивная мощность цепи : Q=3Iф2X=3×40,192×3=14537 вар Полная мощность цепи : 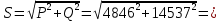 15323 В∙А. 15323 В∙А.Для построения векторной диаграммы найдём длины векторов : ℓUф=Uф/mu=127/40=3.2 см ; ℓIф=Iф/mI=40.19/10=4 см. Построение диаграммы начинаем с построения векторов фазных напряжений UA, UB и UC , которые откладываем под углом 120° относительно друг – друга, предварительно отложив вектор UA вдоль вещественной оси. Вектора фазных токов откладываем под углом φ=53° от соответствующих фазных напряжений. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений.  б) Решение Ток в линейных проводах А и С при обрыве линейного провода В. Так как сопротивление фазы Zb = ¥ (IВ = 0), а Za =Zc включены последовательно на линейное напряжение UCA = UЛ = 220 B; IA = IC = I = UCA/(Za + Zc) = 220/(3.16 + 3.16) = 34.8 А. Напряжение на фазах потребителя при обрыве линейного провода В (нейтральная точка п в этом случае соответствует середине вектора линейного напряжения UCA): Ua = Uc = UCA/2 = 220/2 = 110 B. 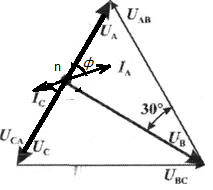 Напряжение между проводом фазы В и нейтральной точкой п определяют из векторной диаграммы: Uc = Uл cos p/6 = 220 × 0.866 = 190,5 B. Активная мощность цепи : P=2Iф2R=2×34.82×1=2422.08 Вт. Реактивная мощность цепи : Q=2Iф2X=2×34.82×3=7266.24 вар Полная мощность цепи : 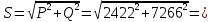 7659 В∙А. 7659 В∙А.в) при коротком замыкании Zb = 0 и Ub = 0, нейтральная точка п переместится в точку В, при этом фазные напряжения Uc = UBC, Uа = UАВ, т.е. фазные напряжения равны линейным напряжениям (Uф = UЛ). При этом фазные токи: IA = IC = Uл/R = 220/3,16 = 69,62 А. Ток IВ при коротком замыкании в соответствии с первым законом Кирхгофа для нейтральной точки п: IA + IB + IC = 0 или - IB = IA + IC. Из прямоугольного треугольника на векторной диаграмме рис. 3.19 имеем: (-IB/2)2 + (IA/2)2 = I2 А, откуда IB =  IA = IA =  × 69,62 ≅ 120,59 А. × 69,62 ≅ 120,59 А. Активная мощность цепи : P=2Iф2R=2×69,622×1=9694 Вт. Реактивная мощность цепи : Q=2Iф2X=2×69,622×3=29082 вар Полная мощность цепи : 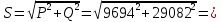 30655 В∙А. 30655 В∙А.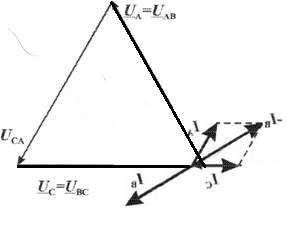 |
