|
|
Геометрия. Резюме теоретической части
Наименование и номер (уникальный номер)
|
Текст Т-2
|
Общая информация об элементе (название элемента, КЭС)
|
Резюме теоретической части (конспект)
Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений
|
Материалы задания
Резюме теоретической части (конспект)
|
Тема: Теорема о пересечении высот треугольника
Содержание модуля (краткое изложение модуля):
Вспомним определение:
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
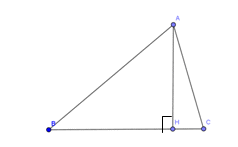
AH – высота треугольника ABC.
Из курса 7 класса, мы знаем, что в любом треугольнике можно провести три высоты.
Теорема: высоты треугольника (или их продолжения) пересекаются в одной точке
Дано: ∆ABC, AA1, BB1, CC1 – высоты треугольника
Доказать: AA1 ∩ BB1 ∩ CC1 = O
Доказательство:
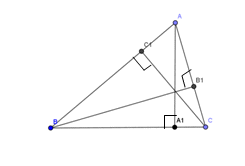
Рассмотрим треугольник, в котором проведены высоты.
Через каждую вершину треугольника AВС проведем прямую, параллельную противоположной стороне.
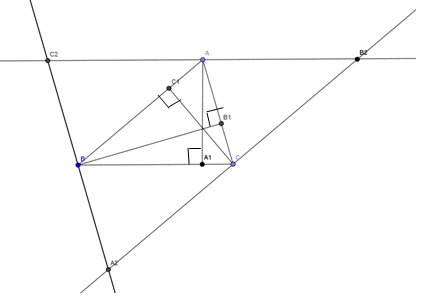
A2B2 ⃦ AB, A2C2 ⃦ AC, B2C2 ⃦ BC
ABCA2 – параллелограмм, значит AC = BA2, AB = CA2
ACBC2 – параллелограмм, значит AC = BC2, BC = AC2
CBAB2 – параллелограмм, значит BC = AB2, AB = CB2
Таким образом
AB = A2C = CB2, значит C – середина отрезка A2B2.
B – середина С2A2
A – середина B2C2
Следовательно
CC1 ⊥ A2B2,
AA1 ⊥ B2C2,
BB1 ⊥ A2C2
Получаем
AA1, CC1, BB1 – серединные перпендикуляры к сторонам ∆A2B2C2 значит
AA1 ∩ BB1 ∩ CC1 = O.
Что и требовалось доказать.
Обратим внимание на формулировку теоремы: высоты треугольника (или их продолжения) пересекаются в одной точке.

Для тупоугольного треугольника пересекаются в одной точке именно продолжения высот.

Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.
|
Опишите, как элемент должен отображаться и располагаться в рамках конкретной сцены
|
Отображение и расположение элемента в соответствии с дизайном портала РЭШ.
| |
|
|
 Скачать 0.49 Mb.
Скачать 0.49 Mb.