расчетно-графическое задание по физике. ргз физ. Шифр группы) (подпись) (Ф. И. О
 Скачать 396.78 Kb. Скачать 396.78 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА По дисциплине Физика (наименование учебной дисциплины согласно учебному плану) Выполнил: студент гр. ГНГ-22 Подопригорова А.А. (шифр группы) (подпись) (Ф.И.О.) Оценка: Дата: Проверил руководитель работы: доцент Мацкевич Е.Е. (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 Колеса радиуса R вращается с угловым ускорением . Найти для точек на ободе колеса к концу n-ой секунды после начала движения: угловую и линейную скорости, тангенциальное, нормальное и полное ускорения, угол, составляемый вектором полного ускорения с радиусом колеса.
 ; ; , так как колесо начинает движение из состояния покоя - , так как колесо начинает движение из состояния покоя -  => => ; ;  ; ;  ; ; и  з рисунка видно, что угол образованный вектором полного ускорения колеса и его радиусом, равен углу между вектором полного ускорения и вектором нормального ускорения, значит, его можно найти из треугольника ускорений: з рисунка видно, что угол образованный вектором полного ускорения колеса и его радиусом, равен углу между вектором полного ускорения и вектором нормального ускорения, значит, его можно найти из треугольника ускорений:  Ответ: 6 рад/с; 5,76 м/с2; 0,48 рад/с2; 5,78 м/с2; 0,96м/с; 5 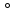 . .Зависимость пройденного телом пути от времени дается уравнением: 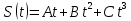 , где A, B, C - некоторые постоянные. Найти зависимость скорости и ускорения от времени; расстояние, пройденное телом, скорость и ускорение тела через время t после начала движения. , где A, B, C - некоторые постоянные. Найти зависимость скорости и ускорения от времени; расстояние, пройденное телом, скорость и ускорение тела через время t после начала движения.
 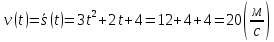  Ответ:  ; ;  . .Груз массой m, привязанный к резиновому шнуру длиной 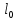 , отклоняют на угол 90 градусов и отпускают. Найти длину резинового шнура , отклоняют на угол 90 градусов и отпускают. Найти длину резинового шнура  в момент прохождения грузом положения равновесия. Жесткость шнура k. в момент прохождения грузом положения равновесия. Жесткость шнура k.
В процессе движения на шарик действует сила тяжести, которая является консервативной и сила упругости. Рассмотрим работу силы упругости на всей траектории движения шарика: во время движения по дуге окружности вектор силы, направленный к центру окружности (против направления деформации), перпендикулярен вектору скорости, который направлен по касательной к окружности, значит, работа силы упругости на этом промежутке равна нулю. Однако по условию шнур растягивается, следовательно, будет происходить перемещение по вертикали на некую величину  , модуль работы силы упругости станет равен: , модуль работы силы упругости станет равен:  . .  Тогда запишем закон сохранения механической энергии с учётом работы неконсервативных сил: 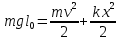 В момент прохождения шариком положения равновесия на него действует сила тяжести и сила упругости, центростремительное ускорение направлено к центру. Запишем второй закон Ньютона:  Мы имеем систему двух уравнений с двумя неизвестными, так как  . Решим её: . Решим её:       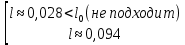 Ответ: 9,4 см. Карандаш длины l, поставленный вертикально, падает на стол. Какую угловую и линейную скорости будет иметь середина и верхний конец карандаша в момент падения?
Центр тяжести карандаша находится на высоте  => => 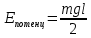 . . , так как карандаш вращается вокруг неподвижной оси, момент инерции найдём по теореме Штейнера: , так как карандаш вращается вокруг неподвижной оси, момент инерции найдём по теореме Штейнера: где момент инерции стержня: где момент инерции стержня:  , , 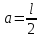 => =>  По закону сохранения механической энергии:  => =>  так как так как 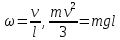 . .Отсюда:  Угловая скорость по определению есть:  , в обоих случаях точки на карандаше проходят одинаковый угол ( , в обоих случаях точки на карандаше проходят одинаковый угол ( ) за одинаковое время ( ) за одинаковое время ( ), значит: ), значит: , соответственно , соответственно  . .Ответ:  . .Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m1 и m2 (m1 > m2). Масса блока m. Найти ускорение грузов  . .
 ешение: ешение: Момент инерции диска:  Двигаться диск с угловым ускорением заставляют моменты сил натяжения нити: 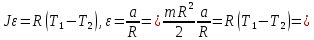  Запишем 2-ой закон Ньютона для каждого из грузов и выразим  : :    Подставим полученное выражение в уравнение для момента инерции диска:  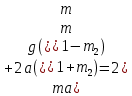   Ответ: 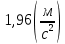 . .На краю платформы массы M, имеющей форму диска, вращающейся вокруг вертикальной оси с частотой 1 , стоит человек массой m. Когда человек перешел в центр платформы, она стала вращаться с частотой 2 . Момент инерции человека рассчитывается как момент инерции материальной точки.
Запишем закон сохранения момента импульса,   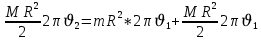   Ответ:  Идеальная тепловая машина работает по циклу Карно. Воздух при давлении p1 и температуре T1 занимает объем V1. После изотермического расширения воздух занял объем V2, после адиабатического расширения объем возрос до V3. Найти: параметры пересечения изотерм и адиабат; работу, совершаемую на каждом участке цикла; полную работу за цикл; КПД цикла; количество теплоты, полученное в цикле от нагревателя, и количество теплоты, отданное холодильнику.
Координаты пересечения изотерм и адиабат: Из уравнения Бойля-Мариотта для изотермического процесса:  Из..уравнения Пуассона для адиабатического процесса:   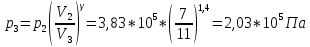 Температура холодильника:  Объём в конце изотермического сжатия: 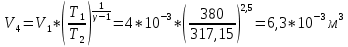 Давление в конце изометрического сжатия:  Параметры пересечения изотерм и изобар: 1) p1 = 6,7  Па; V1 = 4 Па; V1 = 4  ; T1 = 380 К ; T1 = 380 К 2)  ; V2=7 ; V2=7 T1 = 380 К T1 = 380 К3)  ; V3 = 11 ; V3 = 11  ; ;  4)  ; V4 = 6,3 ; V4 = 6,3  ; ;  Работа на участке 1-2 при изометрическом расширении:  Работа на участке 2-3 при адиабатическом расширении (равно противоположному по знаку изменению внутренней энергии):  Работа на участке 3-4 при изотермическом сжатии:  Работа на участке 4-1 при адиабатическом сжатии (равна изменению внутренней энергии):  Полная работа:  КПД цикла:  Кол-во теплоты, полученное от нагревателя:  Кол-во теплоты, отданное холодильнику (из закона сохранения энергии):  Ответ:  Найти изменение энтропии при превращении массы m льда ( Tл ) в пар ( Tп ).
1)Нагревание льда:  2)Плавление льда:  3) Нагревание воды:  4) Испарение воды: 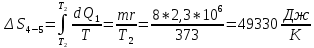 5) Нагревание пара:   Ответ:  . . |



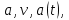

 кг
кг