парадоксы и софизмы. Содержание Введение 3 Глава I. Парадоксы
 Скачать 333.61 Kb. Скачать 333.61 Kb.
|
|
Содержание Введение 3 Глава I. Парадоксы 4 1.1. Понятие парадокс 4 1.2. Парадоксы в математике 4 1.3. Примеры математических парадоксов 5 Глава II. Софизмы 6 2.1. Понятие софизм 6 2.2. Актуальность изучения софизмов 7 2.3. Причины появления софизмов 7 2.4. История возникновения софизмов 8 2.5. Практическое применение и польза софизмов 9 2.6. Софизмы в математике 10 2.6.1. Алгебраические и арифметические софизмы. Примеры. 10 2.6.2. Геометрические софизмы. Примеры 10 2.7. Софизмы, на которые до сих пор нет ответов 11 2.8. Основные ошибки в софизмах 12 Глава III. Исследовательская часть 13 Заключение 14 Источники 15 Приложение 16 Введение История математики полна неожиданных и интересных софизмов и парадоксов. И зачастую именно их разрешение служило толчком к новым открытиям, из которых в свою очередь произрастали новые софизмы и парадоксы. В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости в математических рассуждениях и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играли непреднамеренные ошибки в математических доказательствах, допускаемые даже выдающимися математиками. Большинство софизмов известно очень давно, и можно найти в различных сборниках, журналах. Некоторые из них передаются устно из поколения в поколение. История парадоксов столь же древняя, как история логики, софистики и философии. Но, возможно, наибольшее их количество и разнообразие обнаружено в XX веке. Роль парадоксов столь значительна в познании, что, например, В.С.Библер назвал всю философскую логику логикой парадокса. Цели: - Изучить данную тему, а именно, узнать, что такое софизмы и парадоксы. - В чем причины возникновения софизмов? - Какие различают виды софизмов и парадоксов? - Как их распознать и для чего это нужно? Задачи: Познакомиться с парадоксами и софизмами; узнать, в чем их отличие. Понять, как найти ошибку во внешне безошибочных рассуждениях? Узнать, как проклассифицировать «парадоксы» и «софизмы», по каким критериям? Найти математические парадоксы и софизмы; Обобщить найденный материал. Глава I. Парадоксы 1.1. Понятие парадокс Парадоксы (логики и теории множеств) — (греч. — неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики. Классификация парадоксов: логические (парадокс крокодила, парадокс кучи) математические (парадокс лжеца) вероятноственые парадоксы (парадокс дней рождений) биологические (французский парадокс) И многие другие. Парадокс – это противоречие, которое возникает в ходе рассуждений, важно отметить, что появляется оно само собой, то есть непреднамеренно 1.2. Парадоксы в математике Парадоксы были типичными способами постановки проблем в античном мышлении. Сначала парадоксы рассматривались только как продукт философских измышлений, теперь наука признала их полноправными членами сообщества научных проблем. Парадоксы возникают в современных прикладных науках также часто, как и в древних. В VII в. до н. э. вавилонские жрецы-астрологи заметили, что некоторые планеты временами замедляют движение, пятятся назад, а затем снова продолжают движение в обычном направлении. ГераклидПантийский смог объяснить "явление блуждающих светил" с помощью математической теории эпицикла. Но при этом оставались другие проблемы - не все светила вели себя по этой схеме. Долгое время ученые с помощью своих теорий (геометрическая, механическая) не могли объяснить "дуализм света" (XVIII-XIX вв.), только предположение Д.К. Максвелла о электромагнитной природе света разрешило эту проблему. Таким образом, можно считать, что парадоксы возникают в науке там, где теория не описывает процессы должным образом. Разрешение таких парадоксальных явлений ведет в свою очередь к возникновению новых теорий. 1.3. Примеры математических парадоксов Парадокс лжеца Если утверждение на картинке истинно, значит, исходя из его содержания, верно то, что оно — ложно; но если оно — ложно, тогда то, что оно утверждает, неверно; значит, неверно, что утверждение на картинке — ложно, и, значит, это утверждение истинно. Парадокс лжеца демонстрирует расхождение разговорной речи с формальной логикой, вводя высказывание, которое одновременно и истинно и ложно. В рамках формальной логики данное утверждение не доказуемо и неопровержимо, поэтому решения данного парадокса не существует, но существуют различные варианты его устранения. Для этого можно применить такие рассуждения: положим, что утверждение истинно на 0,5, тогда оно и ложно на 0,5, то есть не всякую фразу можно назвать целиком ложной или целиком истинной — «в чем-то высказывание на картинке лжет, а в чем-то — говорит правду» К такому же выводу можно прийти с помощью тройственной логики. В ней есть три степени истинности: «истина», «ложь» и «неопределенно». Под «неопределенно» понимается промежуточное по смыслу значение между истиной и ложью. К данной степени истинности и относят парадокс лжеца. Как уже говорилось это не решения парадокса лжеца, а всего лишь объяснения, почему данный парадокс возникает в классической двузначной логике высказываний. Они свидетельствует, что строгое деление всех высказываний на истинные и ложные в данном случае неприменимо, поскольку ведет к парадоксу. В настоящее время многие придерживаются такой точки зрения, что данное высказывание вообще не является логическим утверждением, и применять к нему классические методы формальной логики бессмысленно. Глава II. Софизм 2.1. Понятие софизм Слово «софизм» красивое и весьма необычное, к тому же его мы не употребляем в повседневной жизни, поэтому некоторые люди не знают, что оно означает, а, порой, и впервые слышат. Углубимся в историю и выясним: что такое «софизмы»? и откуда к нам пришел этот интересный термин? Истоки софизмов лежат в Древней Греции, где они имели тесную связь с философией и мудрыми учителями, обучавшими желающих искусству логики, риторики и философии. Главной задачей любого софиста было обучить своих учеников доказывать любое своё утверждение, чтобы иметь возможность выйти из любого спора. Достижение этой цели могло осуществляться за счёт различных приёмов – логических, психологических и риторических. Также необходимо отметить, что все софисты имели одну очень интересную идею – все они считали, что в действительности вообще не существует никакой истины, то есть для каждого человека истина своя. Философ Сократ не стал поддерживать идею софистов – он считал бесспорным существование истины, но говорил о том, что она никому неизвестна. Он называл целью существования человека именно поиск единой для всех истины. Это повлекло за собой возникновение спора между софистами и Сократом, на самом деле он продолжается и сейчас. Ну так что же такое софизм? Софизм – это умозаключение, являющееся ложным, но при этом вызывающее иллюзию логичности при поверхностном рассмотрении. Причиной неправильного восприятия является неправильное понятие логических тождеств. Классификация софизмов: Алгебраические – являются ошибками в числовых выражениях, а также уравнениях. Скрыты намеренно. Арифметические – выражения чисел с ошибкой, которую нельзя заметить сразу. Геометрические – заведомо неправильный вывод о геометрических фигурах. Другие: Исторические Психологические Логические Др. Многие софизмы могут быть максимально абсурдными – в этом случае рассуждать о них гораздо проще рассуждать и разоблачать их. Кроме того, часть из них выглядит лишённой всякого смысла и цели. 2.2 Актуальность изучения софизмов Итак, софизм – что это? Прием, помогающий в споре, или бессмысленные рассуждения, не дающие никакого ответа и потому не имеющие ценности? И то, и другое. Что появилось, благодаря софистам? Абстрагирующая деятельность, объектом которой стал язык. В словесных упражнениях, какими были софистические рассуждения, неосознанно отрабатывались первые, еще не ловкие приемы логического анализа языка и мышления. А превращение языка в серьезный предмет особого анализа, в объект систематического исследования было первым шагом в направлении создания науки логика. Софизмы содействовали строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Действительно, уяснение ошибок в математическом рассуждении часто содействовало развитию математики. Особенно поучительна в этом отношении история аксиомы Евклида о параллельных прямых. Одна из формулировок этой теоремы такова: «Через данную точку, лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной». Это утверждение на протяжении более чем двух тысячелетий пытались доказать, т.е. вывести из остальных аксиом многие выдающиеся математики. Поясним, что аксиомой называется исходное положение, принимаемое без доказательств. Все попытки доказать V постулат Евклида не увенчались успехом. Однако, многочисленные «доказательства» этого постулата принесли немало пользы. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики и, кроме того, показывают, что математика – это живая наука. Понятно, что, отыскивая ошибку в «доказательстве» утверждения, что половина равна целому, мы не обязательно откроем новое направление в математике, но задуматься над законами логики и языка ведь тоже полезно? Значит, софизмы все-таки внесли свой вклад в развитие математики. 2.3. Причины появления софизмов К психологическим причинам софизмов относят интеллект человека, его эмоциональность и степень внушаемости. То есть более умному человеку достаточно завести своего оппонента в тупик, чтобы тот согласился с предложенной ему точкой зрения. Чем более убедительной будет речь человека, тем больше шанс, что окружающие не заметят ошибок в его словах. На это и рассчитывают многие из тех, кто пользуется такими приемами в споре. Развитая интеллектуальная личность имеет возможность следить не только за своей речью, но еще и за каждым аргументом собеседника, обращая при этом свое внимание на аргументы, приводимые собеседником. Такого человека отличает больший объем внимания, умение искать ответ на неизвестные вопросы вместо следования заученным шаблонам, а также большой активный словарный запас, при помощи которого мысли выражаются наиболее точно. Объем знаний тоже имеет немаловажное значение. Умелое применение такого вида нарушений, как софизмы в математике, недоступно малограмотному и не развивающемуся человеку. Во время обсуждения точек зрения происходит воздействие не только на разум и чувства, но еще и на волю. Уверенный в себе и напористый человек с большим успехом отстоит свою точку зрения, даже если та была сформулирована с нарушением логики. Особенно сильно такой прием действует на большие скопления людей, подверженных эффекту толпы и не замечающих софизм. Что это дает оратору? Возможность убедить практически в чем угодно. Еще одной особенностью поведения, позволяющей победить в споре при помощи софизма, является активность. Чем более пассивен человек, тем больше шансов убедить его в своей правоте. Какой можно из этого сделать вывод? Эффективность софистских высказываний зависит от особенностей обоих людей, задействованных в разговоре. При этом эффекты всех рассмотренных качеств личности складываются и влияют на исход обсуждения проблемы. 2.4. История возникновения софизмов Софизмы появились в Древней Греции. Они тесно связаны с философской деятельностью софистов — платных учителей мудрости, учивших всех желающих философии, логике и, особенно, риторике (науке и искусству красноречия). Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Первая в истории проба проведения "логической профилактики" в Евклид математике принадлежит гениальному древнегреческому математику - Эвклиду. Он создал удивительный сборник "Псевдарий", где помещая разнообразные ошибочные рассуждения, к которым часто приходят те, кто начинает играть в математику. Таким образом, Эвклид был автором первого из известных сборников математических софизмов и парадоксов. Софистам идейно противостоял знаменитый греческий философ Сократ. Дискуссия между софистами и Сократом о существовании объективной истины зародилась приблизительно в V в. до н.э. Наши дни: появление мысли о том, что человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искуснее замаскирована ошибка, тем больше удовлетворения приносит он тому, кто разгадал его, так как это - маленькое открытие и прекрасная школа, культура математических вычислений. 2.5. Практическое применение и польза софизмов Разбор софизмов прежде всего развивает логическое мышление, т. е. прививает навыки правильного мышления. Обнаружить ошибку в софизме - это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Когда ребенок раз притронется к горячему предмету, то впоследствии он постарается этого не делать. Он будет много осторожнее. Так изучающий математику впоследствии проявит больше осторожности. Далее, что особенно важно, разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций. Все это нужно и важно. Наконец, разбор софизмов увлекателен. Только очень сухого человека не может увлечь интересный софизм. Как приятно бывает обнаружить ошибку в математическом софизме и тем как бы восстановить истину в ее правах. И чем труднее софизм, тем большее удовлетворение доставляет его анализ. Имеется немало разных книг, в которых собраны различные софизмы. В конце XIX - начале XX в. особенно большой известностью среди учащихся пользовалась книга Обреимова "Математические софизмы". Этой книжкой зачитывались. Трудно было найти гимназиста, который не читал бы ее. Василию Ивановичу Обреимову, передовому, революционно настроенному деятелю народного образования последних десятилетий XIX и начала XX в. удалось собрать и обработать интересные софизмы. Наверное, этот сборник софизмов имел в виду В. И. Ленин, когда он в одной из своих статей писал, что такие сборники учащимся "приносят свою пользу". В. И. Ленину в борьбе, которую он вел с врагами рабочего класса, часто приходилось разбирать и разоблачать разнообразные политические софизмы своих противников. Рассуждения по вопросам политики, содержащие замаскированные ошибки, В. И. Ленин сравнивал с математическими софизмами. Он говорил, что эти рассуждения похожи, "...как две капли воды, на те рассуждения, которые математики называют математическими софизмами и в которых, - строго логичным, на первый взгляд, путем, - доказывается, что дважды два пять, что часть больше целого и т. д."*. Эти слова В. И. Ленина показывают, что он знал математические софизмы и это знание помогало ему разоблачать софизмы в политике. 2.6. Софизмы в математике 2.6.1. Алгебраические и арифметические софизмы. Примеры Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях. Всякое число равно своему удвоенному значению. Запишем очевидное для любого числа a тождество a2 - a2 = a2 - a2, вынесем a в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим a(a – a) = (a + a)(a - a).Разделив обе части на a - a, получим a = a + a, или a=2a. Итак, всякое число равно своему удвоенному значению. Разбор софизма. Здесь ошибочен переход к равенству a=2a. В самом деле, число a-a, на которое делится равенство a(a – a) = (a + a)(a - a) равно нулю. Поэтому его можно записать в виде, откуда, очевидно, следует, что число a слева и число a+a справа могут принимать любые, отнюдь не равные друг другу значения. Деление же обеих частей этого равенства на неравное нулю число a-a приводит к бессмыслице. 2.6.2. Геометрические софизмы. Примеры Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними. «Загадочный треугольник» Дан прямоугольный треугольник 13*5 клеток, составленный из четырёх фигур. (Рис. 1) После перестановки фигур при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка. Но мы же понимаем, что такого быть не может. (Рис. 2) Ошибка: (Рис. 3) Площади закрашенных фигур, конечно, равны между собой (оба по 32 клетки), однако, то, что визуально наблюдается как треугольники 13*5, на самом деле таковым не является, и имеет разные площади. То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура названа треугольником (на самом деле являющаяся вогнутым четырёхугольником). Это отчётливо заметно на рис. 2 – гипотенузы верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями. Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2\3 и 5\8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Если нижние стороны этих треугольников параллельны, то гипотенузы в обоих треугольниках 13*5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем – наружу). Если наложить верхнюю и нижнюю фигуры 13*5 друг на друга, то между их гипотенузами образуется параллелограмм, в котором и содержится «лишняя» площадь. На рис. 3 этот параллелограмм приведён в верных пропорциях. Официальным автором этой задачи про «загадочные треугольники» является иллюзионист-любитель Пол Керри, придумавшим этот софизм в XX веке. 2.7. Софизмы, на которые до сих пор нет ответов «Ахиллес никогда не догонит черепаху». Образ Ахиллеса взят из «Илиады» Гомера, где герой Ахиллес неоднократно именуется «быстроногим». Сюжет софизма напоминает безуспешную погоню Ахиллеса за Гектором: «Гектора ж, в бегстве преследуя, гнал Ахиллес непрестанно. Словно как пёс по горам молодого гонит оленя…» Древнегреческий философ Зенон доказывал, что Ахиллес, один из самых сильных и храбрых героев, осаждавших древнюю Трою, никогда не догонит черепаху, которая, как известно, отличается крайне медленной скоростью передвижения. Вот примерная схема рассуждений Зенона. Предположим, что Ахиллес и черепаха начинают движение одновременно, и Ахиллес стремится догнать черепаху. Примем для определённости, что Ахиллес движется в 10 раз быстрее черепахи, и что их отделяют друг от друга 100 шагов. Когда Ахиллес пробежит расстояние в 100 шагов, отделяющие его от того места, откуда начала двигаться черепаха, то в этом месте он уже её не застанет, так как она пройдёт вперёд расстояние в 10 шагов. Когда Ахиллес пробежит и эти 10 шагов, то и там черепахи уже не будет, поскольку она успеет перейти на 1 шаг вперёд. Достигнув и этого места, Ахиллес опять не найдёт там черепахи, потому что она успеет пройти расстояние, равное 1/10 шага, и снова окажется несколько впереди его. Это рассуждение можно продолжать до бесконечности, и придётся признать, Что быстроногий Ахиллес никогда не догонит медленно ползающую черепаху. Где ошибка? Рассматриваемый софизм Зенона даже на сегодняшний день далёк от своего окончательного разрешения. Вот некоторые его аспекты, указанные в книге Мадера А. Г., Мадера Д. А. «Математические софизмы»: «Сначала определим время t, за которое Ахиллес догонит черепаху. Оно легко находится из уравнения a+vt=wt, где a – расстояние между Ахиллесом и черепахой до начала движения, v и w – скорости черепахи и Ахиллеса соответственно. Это время при принятых в софизме условиях (v=1 шаг/сек и w=10 шагов/сек) равно 11,111111… сек. Другими словами, примерно через 11,1 сек. Ахиллес догонит черепаху. Подойдём теперь к утверждениям софизма с точки зрения математики. Проследим логику Зенона. Предположим, что Ахиллес должен пройти столько же отрезков, сколько их пройдёт черепаха. Если черепаха до момента встречи с Ахиллесом пройдёт m отрезков, то Ахиллес должен пройти те же m отрезков плюс ещё один отрезок, который разделял их до начала движения. Следовательно, мы приходим к равенству m=m+1, что невозможно. Отсюда следует, что Ахиллес никогда не догонит черепаху. Итак, путь, пройденный Ахиллесом, состоит из бесконечной последовательности отрезков, которые принимают бесконечный ряд значений. Трудности, которые возникают при оперировании понятиями «непрерывного» и «бесконечного» до сих пор не определены, а разрешение противоречий, содержащихся в них, послужило более глубокому осмыслению основ математики». В действительности, трудно представить себе Ахиллеса, бежавщего расстояние в одну тысячную миллиметра. Таким образом, становится совершенно ясно, что этот софизм Зенона оказывается правильным в теории, но абсолютно неверным в практике. 2.8. Основные ошибки и приемы в софизмах • деление на 0; • неправильные выводы из равенства дробей; • неправильное извлечение квадратного корня из квадрата выражения; • нарушения правил действия с именованными величинами; • путаница с понятиями “равенства” и “эквивалентность” в отношении множеств; • проведение преобразований над математическими объектами, не имеющими смысла; • неравносильный переход от одного неравенства к другому; • выводы и вычисления по неверно построенным чертежам; • ошибки, возникающие при операциях с бесконечными рядами и предельным переходом. Глава III. Исследовательская часть Чтобы показать и подтвердить значимость софизмов и парадоксов в жизни, я провела исследовательскую работу в сфере учебной деятельности (приложение). Данная работа была направлена на развитие умения находить ошибку, анализировать и устранять ее; на развитие логического мышления; на формирование математической грамотности учащихся. Исследование проводилось среди учащихся шестого, седьмого, восьмого и одиннадцатого классов. В шестом классе был проведен урок – презентация, посвященный алгебраическим софизмам по теме «Единицы измерения», а в седьмом данного урока не проводилось. Затем по этой теме была проведена самостоятельная работа. По итогам самостоятельных работ средние баллы в каждом из классов разошлись. Так, средний балл в 6 классе составил – 4,2, в 7 – 3,6 (Диаграмма 1). Ни один учащийся из 6 класса не допустил ошибку при решении задач на единицы измерения, когда в 7 классе 2 учащихся (25%) допустили ошибки в решении задач. Такую же работу я провела в 8 и 11 классах, где в первом из них был проведен урок – презентация, посвященный алгебраическим софизмам по теме «Равносильные уравнения», а затем проведена самостоятельная работа в каждом классе. В 8 классе средний балл был равен – 3,9, а в 11 классе – 3,1 (Диаграмма 2). Только один учащийся (14,3%) 8 класса допустил ошибку по данной теме, когда в 11 ошибки допустили 2 человек (40%). Все полученные данные мы оформили в виде диаграмм (приложение), которые наглядно показали нам различия по уровню усвоения темы самостоятельной. Таким образом, проанализировав полученные результаты, я сделала вывод, что ученики, разобравшие варианты возможных ошибок, научились находить и устранять их. Ученики, не получившие данной информации, допустили различные ошибки по данной теме. Заключение О математических софизмах можно говорить бесконечно много, как и о математике в целом. Софизмы - это смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Буквально вспомнив, кто же такие были софисты, можно понять, что основной задачей было постижение философии. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений. Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов. По началу, я думала, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, я поняла, что софистика-это целая наука, а именно математические софизмы - это лишь часть одного большого течения. Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам можно научится искать ошибки в рассуждениях других людей, научится 18 грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку. И в конце хотелось бы сказать, что все мои цели, поставленные мной в начале работы, были мной достигнуты. Источники https://infourok.ru/issledovatelskaya_rabota_sofizmy_i_paradoksy-485868.htm «Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003. «Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961. «Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971. «Парадоксы науки». Автор: А.К.Сухотин. Издательство "Молодая гвардия", 1978 г. https://infourok.ru/issledovatelskaya-rabota-po-matematike-na-temu-matematicheskie-sofizmi-i-paradoksi-1986353.html Шамина, В. В. Математические парадоксы и софизмы / В. В. Шамина, В. Е. Матешин, А. А. Ефремова, О. В. Шмелева. — Текст: непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 47-50. — URL: https://moluch.ru/young/archive/9/639/ https://habr.com/ru/post/197578/ Приложение 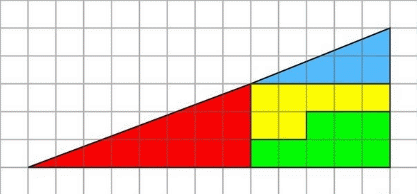 Рис. 1  Рис. 2  Рис. 3 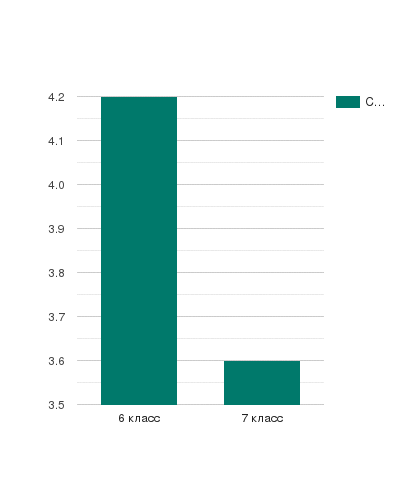 Диаграмма 1 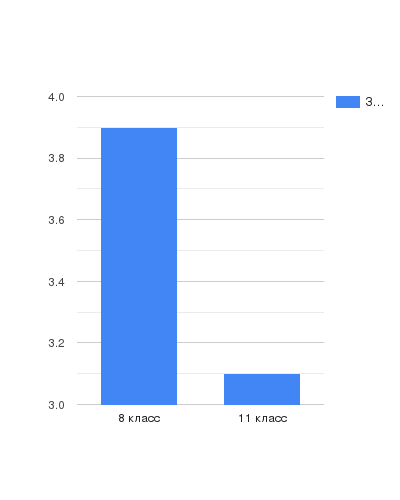 Диаграмма 2 |
