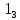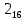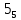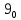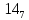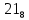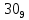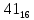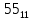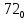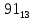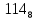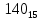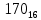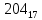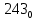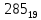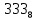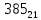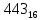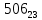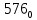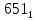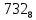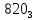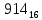Солитер Юля Жанета Артурик. Солитер Игра под названием солитер проводится на доске с тридцатью тремя клетками. Такую доску легко получить, прикрыв шахматную доску листом картона с крестообразным вырезом
 Скачать 21.42 Kb. Скачать 21.42 Kb.
|
|
Солитер Игра под названием солитер проводится на доске с тридцатью тремя клетками. Такую доску легко получить, прикрыв шахматную доску листом картона с крестообразным вырезом.
Требуется снять 31 шашку, причем задаются пустая «начальная» клетка (a,b) и «конечная» (c,d), на которой должна оказаться уцелевшая в конце игры шашка. Правило игры таковы: любая шашка может быть снята с доски. Если рядом с ней (в горизонтальном или вертикальном направлении) находится с одной стороны какая-нибудь шашка («снимающая»), а с противоположной стороны – пустая клетка, на которую «снимающая» шашка должна быть при этом переведена. Из теории игры следует, что решение будет в том и только в том случае, когда a(mod3) и bd(mod3). Приведем для примера решение задачи, в которой клетка (44) является и начальной, и конечной. 64 44 6. 75 73 11. 65 45 16.34-36 56 54 7. 43 63 12. 15 35 17.37-35 44 64 8. 73 53 13. 45 25 18.25-45 52 54 9. 54 52 14. 57 35 19.46-44 73 53 10. 35 55 15. 57 37 20.23-43 21.31-33 27.34-32 22.43-23 28.13-33 23.51-31 29.32-34 24.52-32 30.34-54 25.31-33 31.64-44 26.14-34 Здесь в записи каждого хода указаны для «снимающий» шашки номер исходной клетки и номер клетки, на которую она ставится (при этом с доски снимается шашка, стоящая на промежуточной клетке). Попробуйте снять 31 шашку: а)при начальной клетке (5,7) и конечной (2,4); б)при начальной клетке (5,5) и конечной (5,2). Сложение и вычитание вместо умножения До изобретения таблиц логарифмов для облегчения умножения многозначных чисел применялись так называемые простаферетические таблицы (от греческих слов «простезнс»-прибавление и «афайрезис» - отнятие),представляющие собой Таблицы значения функции 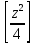 при натуральных значениях z. Так как при α и b целых при натуральных значениях z. Так как при α и b целых 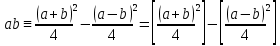 (числа a+b и a-b либо оба четные, либо оба нечетные , в последнем случае дробные части (числа a+b и a-b либо оба четные, либо оба нечетные , в последнем случае дробные части 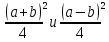 одинаковы),то умножение a на b сводится к определению a+b и a-b и, на конец, разницы чисел одинаковы),то умножение a на b сводится к определению a+b и a-b и, на конец, разницы чисел 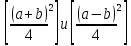 ,взятых из таблицы. ,взятых из таблицы.Для перемножения трех чисел можно воспользоваться тождеством: 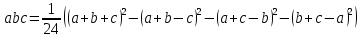 (*) (*)Из которого следует ,что при наличии таблицы значений функции 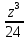 вычисление произведения abc можно свести к определению чисел: a+b+c, a+b-c, a+c-b, b+c-a, и по ним - при помощи таблицы – правой части равенства (*). вычисление произведения abc можно свести к определению чисел: a+b+c, a+b-c, a+c-b, b+c-a, и по ним - при помощи таблицы – правой части равенства (*).Приведем в качестве примера такую таблицу для 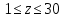 . В таблице даны: . В таблице даны:крупными цифрами – значения 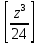 , а мелкими - значения k, где при , а мелкими - значения k, где при 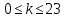 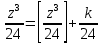 . .
Нетрудно, пользуясь формулой (*) и таблицей, получить: 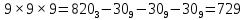 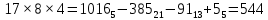 (проверьте!). (проверьте!). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||