Надежность. ДЗ. специальное машиностроение
 Скачать 132.51 Kb. Скачать 132.51 Kb.
|
ФАКУЛЬТЕТ «СПЕЦИАЛЬНОЕ МАШИНОСТРОЕНИЕ» КАФЕДРА «РАКЕТНЫЕ И ИМПУЛЬСНЫЕ СИСТЕМЫ» (СМ-6) ДОМАШНЕЕ ЗАДАНИЕ ПО ДИСЦИПЛИНЕ:
Москва, 2022 г. ЗАДАНИЕ №1 Условие: В течении наблюдаемого периода эксплуатации одного образца РЛС было зарегистрировано 15 отказов. При этом до начала наблюдения станция проработала 258 ч, а к концу наблюдения ее наработка составила 1233 ч. Определить среднюю наработку станции до первого отказа. Решение: Определим сначала наработку наблюдаемого образца РЛС за указанный период (время, за которое производилось наблюдение): 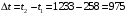 ч. ч.Средняя наработка на отказ (среднее значение наработки восстанавливаемого изделия между отказами) по статистическим данным определяется по формуле: 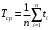 , ,где 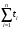 – время исправной работы между (i-1) и i отказами; n – число отказов за наблюдаемое время наработки – время исправной работы между (i-1) и i отказами; n – число отказов за наблюдаемое время наработки 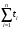 , где n=15. , где n=15.Приняв 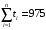 ч, определим среднюю наработку на отказ: ч, определим среднюю наработку на отказ: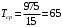 ч. ч.Ответ: 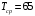 часов. часов.ЗАДАНИЕ №2 Условие: Нерезервированная система управления состоит из n=4000 элементов. Известна требуемая вероятность безотказной работы системы Pc(t) = 0,9 при t = 100 ч. Необходимо рассчитать допустимую среднюю интенсивность отказов одного элемента, считая элементы равнонадежными, для того чтобы приближенно оценить достижение заданной вероятности безотказной работы при отсутствии профилактических осмотров в следующих случаях: а) резервирование отсутствует; б) применено раздельное (поэлементное) дублирование. Решение: А) Резервирование отсутствует Вероятность безотказной работы системы за время t определяется формулой: 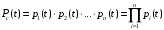 , ,где 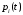 – вероятность безотказной работы i-го элемента. – вероятность безотказной работы i-го элемента.Пусть для элементов справедлив экспоненциальный закон распределения надежности и известны их интенсивности отказов. Тогда и для системы в целом будет справедлив экспоненциальный закон распределения надежности, причем: 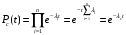 , ,где 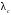 – интенсивность отказов системы, – интенсивность отказов системы, 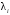 – интенсивность отказов i-го элемента. – интенсивность отказов i-го элемента. Интенсивность отказов нерезервированной системы при основном соединении равна сумме интенсивностей отказов ее элементов: 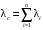 . .Так как, все элементы по условию равнонадежны, то интенсивность отказов системы будет: 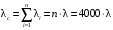 . .Таким образом, отсюда находим интенсивность отказов одного элемента системы, у которой отсутствует резервирование: 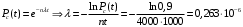 1/час 1/часБ) Применено раздельное дублирование Вероятность безотказной работы системы при раздельном дублировании и равнонадежных элементах равна: 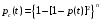 , ,где 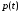 – вероятность безотказной работы одного элемента. – вероятность безотказной работы одного элемента.Так как вероятность безотказной работы системы должна быть 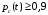 , то , то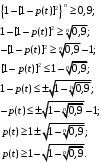 Разложив в ряд Тейлора выражение 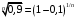 по степеням по степеням 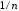 в ряд и пренебрегая членами ряда высшего порядка малости, получим в ряд и пренебрегая членами ряда высшего порядка малости, получим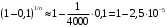 . .Учитывая, что 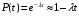 , то интенсивность отказов элементов должна быть , то интенсивность отказов элементов должна быть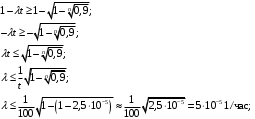 Ответ: а) 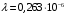 1/час; б) 1/час; б) 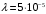 1/час 1/часЗАДАНИЕ №3 Условие: Выборка объемом n =100 устройств подлежит испытанию в интересах заказчика. Браковочное число принято A1=4, а q1 = 0,08. Определить риск β’, исходя из распределения Пуассона. Решение: Риск заказчика определяется следующей формулой для крупносерийных высоконадежных устройств ( 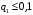 ) исходя из распределения Пуассона: ) исходя из распределения Пуассона: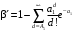 , ,где 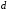 – число дефектных изделий в выборке; – число дефектных изделий в выборке; 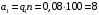 . .Реализовав на языке программирования Python функцию для вычисления риска заказчика, получим: 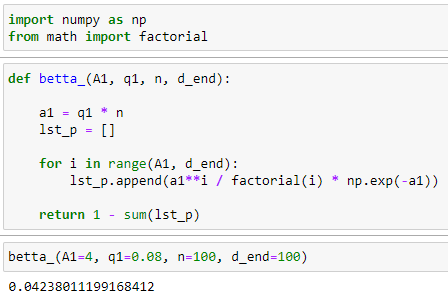 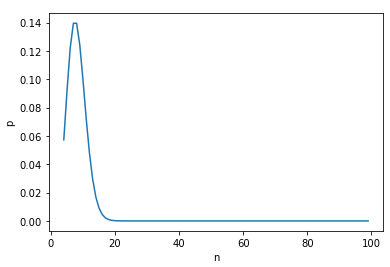 Ответ: 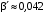 . . |

