Кванторы и Предикаторы РФЭТ. РешениеКванторыПредикаторы. Теория Предикатом называется высказывание, зависящее от переменных
 Скачать 122 Kb.
|
|
Теория: Предикатом называется высказывание, зависящее от переменных Примеры:  -двухместный предикат трехместный предикат -одноместный предикатВысказывание - это 0-местный предикат. При подстановке переменных предикат превращается в высказывание. Например, наш трёхместный предикат при подстановке превратился в истинное высказывание  .К предикатам применимы все операции, которые мы рассматривали применительно к высказываниям. Помимо этих операций к предикатам применимы операции кванторизации. Кванторы  - любой,  - существует. При наложении одного квантора n-местный предикат превращается в n -1 местный. Если переменная связана квантором, то вместо неё нельзя подставлять значения.  - это уже двухместный предикат. В него мы можем подставлять значения вместо  , вместо x ничего подставлять нельзя. Переменная x связана квантором. - это ложное высказывание - это истинное высказывание - это высказывание, т.к. все переменные связаны. Оно ложное.Множество истинности предиката: Это множество значений переменных, при которых предикат обращается в истинное высказывание. Предикаты P и Q, заданные над одним множеством, называются эквивалентными, если их множества истинности совпадают, т.е  Если  , то предикат Q называют следствием предиката P.Задача на кванторы Рассмотрим двухместный предикат  над множеством RС помощью кванторов построим всевозможные высказывания:  «Сумма двух любых чисел равна 7» -это ложное высказывание « Для любого числа x существует число y такое, что в сумме они дают 7» - это истинное высказывание, действительно   «Существует такое число x, что к нему можно прибавить любое число y и в сумме получится 7 – это ложное высказывание «Существует два числа, сумма которых равна 7» - это истинное высказывание, действительно, например  Задача_на_множество_истинности:_изобразите_множества_истинности_следующих_предикатов'>Задача на множество истинности: изобразите множества истинности следующих предикатов   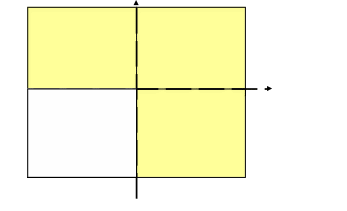  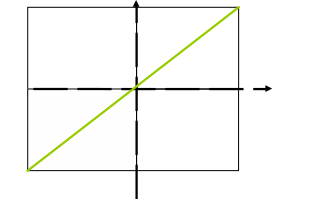    c   над множеством M={1,2,3,4,5,6},   3   изображено на картинкеЗадача. Выяснить, равносильны ли следующие предикаты, если их рассматривать над множеством действительных чисел R, над множеством рациональных чисел Q, над множеством целых чисел Z и над множеством натуральных чисел N.  Рассмотрим предикаты  и  над множеством R   следовательно, предикаты и не равносильны над множеством RРассмотрим предикаты и над множеством Q следовательно, предикаты и не равносильны над множеством QРассмотрим предикаты и над множеством Z  следовательно, предикаты и равносильны над множеством ZРассмотрим предикаты и над множеством N  следовательно, предикаты и равносильны над множеством N |
,