разностные методы решеия задач. Типы уравнений математической физики
 Скачать 76.11 Kb. Скачать 76.11 Kb.
|
|
ГОУВПО «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра прикладной математики и искусственного интеллекта ДОКЛАД На тему «Типы уравнений математической физики» по дисциплине «Разностные методы решения краевых задач» Выполнил: студент группы ПМК-19 Кныш Богдан Юрьевич Преподаватель: Перинская Елена Владимировна Донецк – 2022 Оглавление Введение 3 Классификация уравнений 4 Примеры 16 Список литературы 19 ВведениеСоздание математических моделей различных физических процессов и построение методов решения физических задач является предметом математической физики. Постановка задач математической физики заключается в построении математических моделей, описывающих основные закономерности изучаемых физических явлений. Это моделирование состоит в выводе уравнений, которым удовлетворяют величины, характеризующие данный процесс. При этом исходят из основных физических законов, которые учитывают наиболее существенные черты явления, отвлекаясь от второстепенных характеристик. Многие задачи механики и физики приводят к исследованию дифференциальных уравнений с частными производными. В ряде случаев приходится иметь дело с интегральными и интегро-дифференциальными уравнениями. Однако в этом пособии мы будем рассматривать именно дифференциальные уравнения, как наиболее часто встречающиеся в задачах математической физики. Например, при изучении различных видов волн – упругих, звуковых, электромагнитных, а также других колебательных явлений используется так называемое волновое уравнение. Процессы распространения тепла и явления диффузии описываются уравнением теплопроводности. При рассмотрении установившегося теплового состояния в изотропном теле мы приходим к уравнению Пуассона. Ряд установившихся процессов, в частности таких, как потенциальное движение несжимаемой жидкости или потенциал стационарного электрического тела, приводят к уравнению Лапласа. Уравнения, указанные выше, являются дифференциальными уравнениями в частных производных второго порядка и называются основными уравнениями математической физики. Многочисленные задачи физики и техники приводят к сравнительно небольшому числу типов дифференциальных уравнений с частными производными. Чаще всего встречаются уравнения второго порядка, содержащие частные производные второго порядка, причем линейные по этим производным. Следует отметить, что в отличие от обыкновенных дифференциальных уравнений, общее решение которых зависит от произвольных постоянных, общее решение дифференциальных уравнений с частными производными зависит от произвольных функций. Классификация уравненийБольшинство физических процессов различной природы моделируется дифференциальными уравнениями в частных производных. Наиболее часто при этом встречаются линейные уравнения второго порядка. Их изучение и составляет предмет математической физики. Дифференциальным уравнением в частных производных называется соотношение между искомой функцией нескольких переменных, её частными производными и независимыми переменными. Для двух независимых переменных x и y дифференциальное уравнение в частных производных второго порядка в общем случае имеет вид 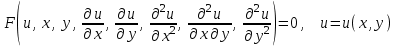 . .Наивысший порядок частных производных, входящих в уравнение, определяет порядок дифференциального уравнения. Уравнение называется линейным, если оно линейно относительно искомой функции и всех её производных. Линейное дифференциальное уравнение в частных производных второго порядка с двумя независимыми переменными имеет следующий вид 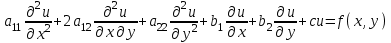 . (1) . (1)Коэффициенты линейного уравнения могут зависеть от переменных x, y. Тогда говорят, что уравнение (1) является уравнением с переменными коэффициентами. Если f(x, y) = 0, то уравнение (1) называется линейным однородным. В противном случае оно будет линейным неоднородным. Все многообразие уравнений математической физики может быть разделено на три класса. Уравнения каждого класса обладают общими свойствами решений. В каждом из этих классов есть простейшее уравнение, называемое каноническим. Принадлежность уравнения тому или иному классу определяется соотношением между коэффициентами при старших производных. Если в некоторой области плоскости x0y дискриминант уравнения (1) 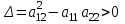 , то говорят, что уравнение (1) будет в этой области уравнением гиперболического типа. , то говорят, что уравнение (1) будет в этой области уравнением гиперболического типа.Если в некоторой области плоскости x0y дискриминант 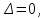 то в этой области уравнение относится к параболическому типу. Наконец, если в некоторой области то в этой области уравнение относится к параболическому типу. Наконец, если в некоторой области 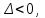 то уравнение в этой области будет уравнением эллиптического типа. то уравнение в этой области будет уравнением эллиптического типа.Основными уравнениями математической физики являются: 1). Волновое уравнение 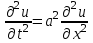 . .Это однородное уравнение гиперболического типа. Оно описывает процессы поперечных колебаний струн, продольные колебания стержней, крутильные колебания валов, колебания тока и напряжения в проводах и другие динамические процессы (здесь и далее x – пространственная координата, t – время). 2). Уравнение теплопроводности 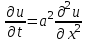 . .Это однородное уравнение параболического типа. Оно описывает процессы распространения тепла в стержнях, задачи фильтрации жидкостей и газов в пористых средах и др. 3). Уравнение Лапласа 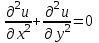 . .Это однородное уравнение эллиптического типа. Уравнение Лапласа не содержит времени (x и y – пространственные координаты) и описывает стационарные процессы в электрических и магнитных полях, задачи стационарной теплопроводности, многие стационарные задачи гидродинамики, диффузии, прочности и др. Любое дифференциальное уравнение математической физики имеет бесчисленное множество решений. Для получения единственного решения необходимо задание дополнительных условий, которые позволяют однозначно описать конкретный физический процесс. Количество и вид этих условий зависят от характера и порядка производных, входящих в уравнение, от формы области, в которой ищется решение уравнения, от характера взаимодействия рассматриваемого тела (или процесса в выделенном теле) с окружающей средой. В общем случае дополнительными условиями могут быть начальные и граничные условия. Начальные условия описывают состояние системы в начальный момент времени. Для уравнения гиперболического типа ставятся два начальных условия соответственно второму порядку производной по времени, входящей в уравнение. Они характеризуют величины отклонений и скоростей точек тела (струны, стержня и др.) в начальный момент времени. Для уравнения параболического типа ставится одно начальное условие, что соответствует первому порядку производной по времени (если искомая функция в уравнении теплопроводности u(x, t) – температура в произвольном сечении стержня в любой момент времени t, то начальным условием задается распределение температуры по длине стержня в начальный момент времени t = 0). Граничные условия для волнового уравнения (если оно описывает, например, поперечные колебания струны конечных размеров) характеризуют поведение концов струны в процессе колебаний и зависят от характера их закрепления. Для уравнения теплопроводности стержня граничные условия имеют существенно различный вид в зависимости от характера теплообмена концов стержня с окружающей средой. Для уравнения эллиптического типа, как и для уравнения параболического типа, также различают разные краевые задачи в зависимости от условий на контуре рассматриваемой области. Так, если на границе Г области задано значение искомой функции: 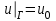 , ,то говорят, что для уравнения Лапласа поставлена первая краевая задача (задача Дирихле). Если на границе области задано значение производной искомой функции по направлению нормали 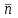 к границе: к границе: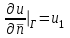 , ,то говорят, что для уравнения Лапласа поставлена вторая краевая задача (задача Неймана). Если на границе области задано условие, связывающее искомую функцию и её производную 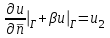 , ,то поставлена третья или смешанная краевая задача. Здесь u0, u1, u2, – непрерывные функции, определённые на границе. Постановка задач математической физики Как видно из приведенных выше примеров общее решение дифференциального уравнения второго порядка с частными производными зависит от двух произвольных функций. На практике интерес представляет не бесчисленное множество функций, являющихся решениями данного уравнения, а одна из них, которая описывает конкретный реальный процесс. Для полного описания реального физического процесса одного дифференциального уравнения мало. Необходимо кроме него задать начальное состояние этого процесса, т.е. его состояние в тот момент времени, когда мы начали его наблюдать (начальное условие). Кроме того, необходимо задать режим на границе той области, в которой этот процесс совершается (граничное условие). Совокупность этих условий называется краевой задачей. В сущности построение математической модели реального физического процесса и заключается в написании дифференциального уравнения, описывающего этот процесс и формулировке начальных и граничных условий, отвечающих этому процессу. Здесь мы изучаем дифференциальные уравнения второго порядка, для неизвестной функции, зависящей от двух независимых переменных. Для таких уравнений различают три типа краевых задач. 1. Задача Коши для уравнений гиперболического типа (см. волновое уравнение) и параболического типа (уравнение теплопроводности). В этом случае область задания уравнения совпадает со всем пространством – граничные условия отсутствуют. Задаются только начальные условия. 2. Краевая задача для уравнения эллиптического типа. Задаются условия на границе области задания уравнения. Начальные условия отсутствуют. 3. Смешанная задача для уравнений гиперболического и параболического типа: задаются начальные и граничные условия. Решение задачи математической физики описывает реальный физический процесс, поэтому оно должна удовлетворять некоторым требованиям. Прежде всего надо убедиться, что решение поставленной краевой задачи существует и единственно. На практике на этот вопрос мы отвечаем, находя решение конкретной задачи. Решение поставленной задачи должно быть устойчивым. Дело в том, что в основе определения физических величин лежит процесс их измерения, который всегда связан с погрешностью измерения. С погрешностью определяются и исходные данные задачи (начальные и граничные условия). Если малые изменения данных задачи влекут за собой малые изменения ее решения, то говорят, что решение краевой задачи устойчиво относительно малых изменений ее данных (непрерывно зависит отданных задачи). В этом случае решение правильно отражает реальный физический процесс. В противном случае решение задачи неустойчивое и неправильно отражает течение физического процесса. Итак, постановка задачи математической физики включает в себя задание дифференциального уравнения в частных производных, описывающего исследуемый процесс, а также в общем случае граничных и начальных условий, позволяющих получить единственное решение. Если задача математической физики поставлена корректно, то её решение существует, единственно и устойчиво к малым изменениям исходных данных. Уравнение математической физики Уравнение с частными производными – уравнение, содержащее неизвестную функцию двух или более независимых переменных и некоторые частные производные этой функции. Обозначим через D - область n-мерного евклидова пространства 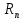 точек x = ( точек x = (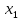 , . . . , , . . . , 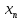 ) 1 , n > 2. Пусть F(x, . . . , ) 1 , n > 2. Пусть F(x, . . . , 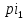 ,...,in , . . .) — заданная гладкая действительная функция точек x области D и действительных переменных ,...,in , . . .) — заданная гладкая действительная функция точек x области D и действительных переменных  с неотрицательными целочисленными индексами с неотрицательными целочисленными индексами 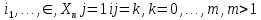 и, по крайней мере, одна из производной которой: и, по крайней мере, одна из производной которой: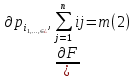 отлична от нуля. Определение 1 Равенство вида: 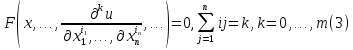 называется дифференциальным уравнением с частными производными порядка m относительно неизвестной функции u(x), x ∈ D. Уравнение с частными производными первого порядка может быть записано в виде: 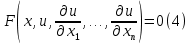 Уравнение с частными производными второго порядка имеет вид: 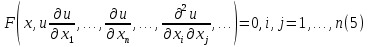 Будем говорить, что мы решили уравнение с частными производными, если найдены все функции u, удовлетворяющие (3) (возможно, лишь в классе функций, удовлетворяющих вспомогательным граничным условиям на некоторой части границы ∂D). Когда мы говорим, что решение найдено, в идеальном случае это означает, что найдены простые явные формулы для решения или, если такое невозможно или слишком сложно, доказано существование решения и установлены его некоторые свойства. Определение 2 Определенная в области D задания уравнения (3) действительная функция u(x), непрерывная вместе со своими частными производными, входящими в это уравнение, и обращающая его в тождество, называется классическим решением (или регулярным решением). Определение 3 Если u(x) регулярное решение уравнения (3), то поверхность u = u(x) в пространстве переменных (x, u) называется интегральной поверхностью уравнения (3). Определение 4 Уравнение с частными производными (9) называется линейным, если функция F(x, . . . , pi1,...,in , . . .) является линейной относительно всех переменных pi1,...,in , 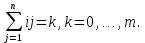 Уравнение вида: 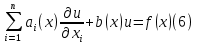 есть линейное уравнение первого порядка, а уравнение: 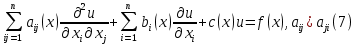 является линейным уравнением второго порядка относительно неизвестной функции u(x). Определение 5 Если функция: 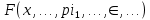 линейна относительно переменных линейна относительно переменных  при: при: 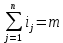 то уравнение (3) называется квазилинейным. Уравнение: 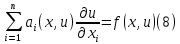 есть квазилинейное уравнение первого порядка A уравнение: 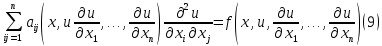 -квазилинейное уравнение второго порядка относительно неизвестной функции u(x). Система уравнений с частными производными — совокупность нескольких уравнений с частными производными относительно нескольких неизвестных функций. Определение 6 Равенство вида: 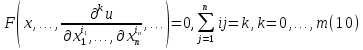 где 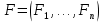 задана, а задана, а 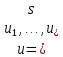 неизвестна, называется системой уравнений с частными производными m–го порядка. Мы будем рассматривать системы, у которых число уравнений s совпадает с числом неизвестных неизвестна, называется системой уравнений с частными производными m–го порядка. Мы будем рассматривать системы, у которых число уравнений s совпадает с числом неизвестных 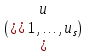 . Обычно рассматриваются именно такие системы, хотя случаи, когда число уравнений меньше или больше числа неизвестных, также исследуются. Очевидно, что можно классифицировать системы по признаку линейности и квазилинейности. Не существует общей теории, устанавливающей разрешимость всех уравнений с частными производными. . Обычно рассматриваются именно такие системы, хотя случаи, когда число уравнений меньше или больше числа неизвестных, также исследуются. Очевидно, что можно классифицировать системы по признаку линейности и квазилинейности. Не существует общей теории, устанавливающей разрешимость всех уравнений с частными производными.Весьма сомнительно, что создание такой теории вообще возможно ввиду большого многообразия физических, геометрических и вероятностных явлений, которые моделируются уравнениями с частными производными. Поэтому исследования концентрируются вокруг некоторых конкретных уравнений, важных для приложений, как в рамках самой математики, так и для смежных дисциплин, с надеждой, что интуитивное понимание истоков этих уравнений с частными производными подскажет путь к их решению. Перечислим некоторые важные в современных исследованиях уравнения с частными производными, с тем, чтобы иметь хотя бы начальное представление (название и вид) об этих хорошо известных уравнениях. Ниже мы обсудим происхождение для уравнений из приведенного ниже списка. Всюду далее x ∈ D, где D — область пространства R n , и t > 0 — время. 1) При изучении различных видов волн — упругих, звуковых, электромагнитных, а также других колебательных явлений мы приходим к волновому уравнению: 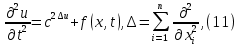 где c — скорость распространения волны в данной среде, f(x, t) — внешняя сила. 2) Процессы распространения тепла в однородном изотропном теле, так же как и явления диффузии, описываются уравнением теплопроводности: 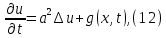 где a — коэффициент температуропроводности, g(x, t) — плотность тепловых источников. 3) При рассмотрении установившихся колебательных явлений или стационарного теплового состояния в однородном изотропном теле мы приходим к уравнению Пуассона: 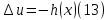 При h( x) = 0 уравнение (3) переходит в уравнение Лапласа: 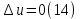 Потенциалы поля тяготения и стационарного электрического поля также удовлетворяют уравнению Лапласа, в котором отсутствуют массы и соответственно электрические заряды. Уравнения (11)-(24) часто называют основными уравнениями математической физики. Их подробное изучение дает возможность построить теорию широкого круга физических явлений и решить ряд физических и технических задач. Каждое из уравнений (11)-(14) имеет бесчисленное множество частных решений. При решении конкретной физической задачи необходимо из всех этих решений выбрать то, которое удовлетворяет некоторым дополнительным условиям, вытекающим из её физического смысла. Итак, задачи математической физики состоят в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям. Такими дополнительными условиями чаще всего являются так называемые граничные условия, т. е. условия, заданные на некоторой части границы рассматриваемой среды, и начальные условия, относящиеся к одному какому-нибудь моменту времени, с которого начинается изучение данного физического явления. Решение однородного уравнения теплопроводности методом разделения переменных (Фурье) Решение начально-краевой задачи строится методом разделения переменных так же, как и решение волнового уравнения. Искомая функция u(x,t) представляется в виде: u(x,t) = X (x)T(t) ≠ 0 Подстановка этого выражения в уравнение приводит к равенству: 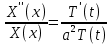 из которого после обычных рассуждений, характерных для метода разделения переменных, следует, что обе части равенства не зависят ни от x, ни от t , следовательно, являются постоянными Обозначая, как и выше, эту постоянную через - 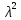 (λ > 0), то есть принимая: (λ > 0), то есть принимая: 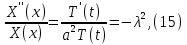 получим два независимых обыкновенных линейных однородных дифференциальных уравнения: 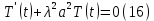 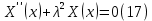 В отличие от волнового уравнения здесь для функции T(t) получается уравнение первого порядка (16). Итак, для определения функции X(x) приходим к задаче на собственные значения что и при решении волнового уравнения. Собственные значения λn и собственные функции этой задачи 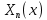 определяются соответственно по формулам: определяются соответственно по формулам: 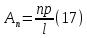 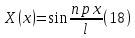 Подставляя (4) в (2), приходим к линейному дифференциальному уравнению первого порядка 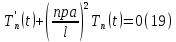 Разделяя переменные в уравнении (19) и интегрируя, находим его общее решение в виде 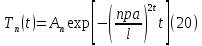 Где, 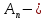 произвольная постоянная произвольная постояннаяНаходим общее решение однородного уравнения теплопроводности: 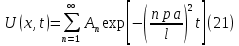 Произвольную постоянную 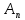 находим далее из условия U( x,0) = находим далее из условия U( x,0) =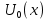 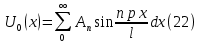 Тогда, 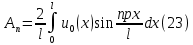 Как видно из (21), решение уравнения теплопроводности носит по времени апериодически затухающий характер, что соответствует выравниванию температуры в стержне с течением времени. Примеры1.Найти закон колебания струны длиной 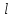 , если в начальный момент струне придана форма кривой , если в начальный момент струне придана форма кривой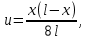 а затем струна отпущена без начальной скорости. Струна закреплена на концах. Внешние силы отсутствуют. Решение. Задача сводится к решению однородного волнового уравнения при однородных граничных условиях: 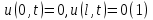 И начальных условиях: 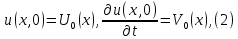 Где 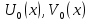 – заданные функции, описывающие соответственно отклонения и скорости точек струны в начальный момент времени. – заданные функции, описывающие соответственно отклонения и скорости точек струны в начальный момент времени.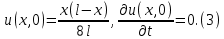 Для рассматриваемого случая, очевидно, 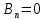 , так как согласно (2) , так как согласно (2) 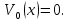 Подставляя в Подставляя в 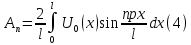 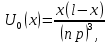 после двукратного интегрирования по частям находим: 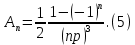 Подстановка (5) в 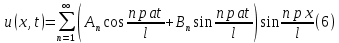 с учетом 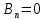 приводит к решению задачи в виде: приводит к решению задачи в виде: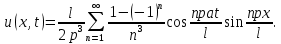 2. Найти функцию u(x, y), удовлетворяющую уравнению Пуассона: 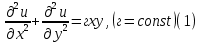 и однородным граничным условиям на прямоугольном контуре: 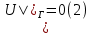 Решение. Будем искать решение задачи (1), (2) в виде разложения в ряд по собственным функциям однородной задачи 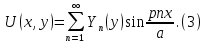 При этом удовлетворяются граничные условия на вертикальных сто- ронах области x = 0 и x = a. Функцию 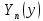 следует определить так, чтобы функция u(x,y) удовлетворяла уравнению (1) и граничным условиям на горизонтальных сторонах: следует определить так, чтобы функция u(x,y) удовлетворяла уравнению (1) и граничным условиям на горизонтальных сторонах: u(x,0) = u(x,b) = 0 . 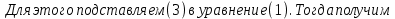 : :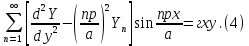 В левой части уравнения имеем ряд Фурье по синусам на отрезке [0,a]. Разложим функцию в правой части (4) также в ряд Фурье по синусам на том же отрезке: 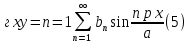 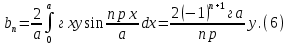 Подставляем выражение (5) с учётом (6) в правую часть уравнения (4): 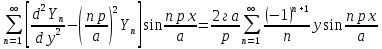 В результате для определения функции 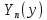 приходим к обыкновенному линейному неоднородному дифференциальному уравнению второго порядка с постоянными коэффициентами: приходим к обыкновенному линейному неоднородному дифференциальному уравнению второго порядка с постоянными коэффициентами: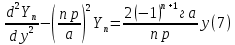 Общее решение уравнения (7) имеет вид: 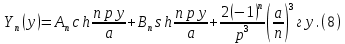 После подстановки (8) в равенство (3) получаем: 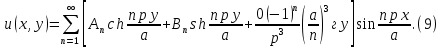 Константы 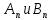 найдём из условия удовлетворения граничным условиям на горизонтальных сторонах области y = 0 и y = b . При y = 0 из условия u(x,0) = 0 имеем: найдём из условия удовлетворения граничным условиям на горизонтальных сторонах области y = 0 и y = b . При y = 0 из условия u(x,0) = 0 имеем: 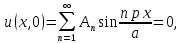 откуда в силу произвольности функции sin 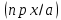 следует следует 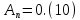 При y = b из условия u(x,b) = 0 с учётом (10) находим 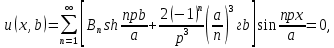 И, следовательно 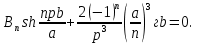 Из последнего равенства определяем: 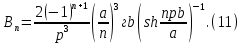 Подставляя (10) и (11) в (9), приходим к решению поставленной задачи в виде: 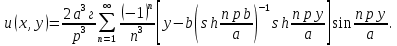 Список литературыБейтман Г. Высшие трансцендентные функции. Т.1 / Г. Бейтман, А. Ердейы. - М .: Н. - 2011. 54 Бицадзе А.Б. Уравнения математической физики. Второй изд. / Бицадзе А.Б. М: Наука, 2012. - 336 с. Боголюбов А.Н. Задачи математической физики: уч. Пособие / А.Н. Боголюбов, В.В. Кравцов. - М: Изд-во МГУ. - 2008. - 350 с. Будак Б.М. Сборник задач по математической физике / Б. Будак, А.А. Самарский, А. Н. Тихонов. М: Наука. - 2012. - 688 с. Будак Б.М. Сборник задач по математической физике / Б. Будак, А.А. Самарский, А. Н. Тихонов. М: Наука. - 2012. - 688 с. Владимиров В.С. Уравнения математической физики / В.С. Владимиров, В.В. Жаринов. М: ФИЗМАТЛИТ, 2010. - 400 с. Владимиров В.С. Уравнения математической физики / Владимиров В.С. М: Наука, 2011. Голубев В.В. Лекции по аналитической теории дифференциальных уравнений / Голубев В.В. - М. - Л .: ГИТТЛ. 2010. - 436 с. Гончаренко В.Н. Основы теории управлений с частными производными / Гончаренко В.Н. - М .: Высшая школа, 2005. - 311 с. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнение в частных производных математической физики / Н.С. Кошляков, Э.Б. Глинер, М.М. Смирнов. М .: Высшая школа, 2010. |
